Файл: kurs-lekcij-po-tau.doc

Таким образом можно определить уравнение динамики реальных звеньев и всей реальной САУ, если оно теоретически это сделать затруднительно. Для снятия частотных характеристик реальной разомкнутой САУ на ее вход подают гармонический сигнал с изменяемой частотой и определяют изменение амплитуды и фазы выходного сигнала в зависимости от частоты. По полученным характеристикам определяют уравнение динамики, после чего САУ можно исследовать теоретически.

7.2. Законы регулирования

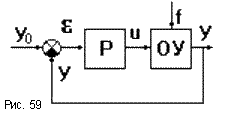
Пусть задана какая-то САР (рис.59).

Законом регулирования называется математическая зависимость, в соответствии с которой управляющее воздействие на объект вырабатывалось бы безынерционным регулятором.

Простейшим из них является пропорциональный закон регулирования, при котором

u(t) = Ke(t) (рис.60а),

где u(t)- это управляющее воздействие, формируемое регулятором,e(t)- отклонение регулируемой величины от требуемого значения,K- коэффициент пропорциональности регулятора Р.

То есть для создания управляющего воздействия необходимо наличие ошибки регулирования и чтобы величина этой ошибки была пропорциональна возмущающему воздействию f(t). Другими словами САУ в целом должна быть статической.

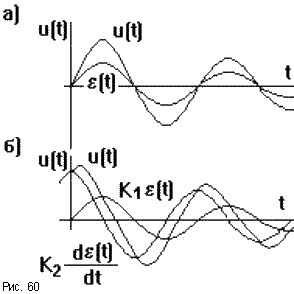
Такие регуляторы называют П-регуляторами.

Так как при воздействии возмущения на объект управления отклонение регулируемой величины от требуемого значения происходит с конечной скоростью (рис.60б), то в начальный момент на вход регулятора подается очень малая величина e , вызывая при этом слабые управляющие воздействия u. Для повышения быстродействия системы желательно форсировать процесс управления.

Для этого в регулятор вводят звенья, формирующие на выходе сигнал, пропорциональный производной от входной величины, то есть дифференцирующие или форсирующие звенья.

Такой закон регулирования называется пропорционально - дифференциальным:

u(t) = K₁e(t) + K₂de(t)/dt.

В соответствии с ним работают ПД-регуляторы.

Чем быстрее нарастает отклонение регулируемой величины от требуемого значения, тем интенсивнее работает ПД-регулятор, что препятствует дальнейшему нарастанию данного отклонения. Кроме того при увеличении отклонения (de(t)/dt > 0) управляющий сигнал u будет больше, чем при уменьшении (de(t)/dt < 0), что также играет положительную роль, снижая колебательность процеса управления.

Добавление в регулятор двух дифференцирующих звеньев позволяет формировать управляющее воздействие по второй производной отклонения e, такой регулятор называется ПДД-регулятором.

Интегральный закон регулированияреализуетсяИ-регулятором, его формулировка:

.

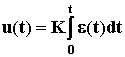Этот регулятор наращивает управляющее воздействие до тех пор пока управляемая величина отличается от требуемого значения, то есть пока e(t)0.

И-регулятор обеспечивает астатическое регулирование.

При малых eуправляющее воздействие изменяется с малой скоростью, поэтому данный регулятор очень инерционный.

Чтобы увеличить быстродействие обычно последовательно с ним включают усилитель, это дает пропорционально-интегральный закон регулирования (ПИ-регулятор), его формула:

.

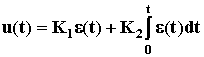Первое слагаемое обеспечивает быстродействие, второе - астатичность, то есть точность регулирования.

Еще большее быстродействие обеспечивается при добавлении слагаемого, пропорционального производной от отклонения управляемой величины de/dt, такой закон регулирования обеспечиваетсяПИД-регулятором, его формула:

.

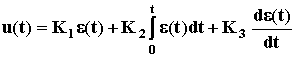Лекция 8.Алгебраические критерии устойчивости

8.1. Понятие устойчивости системы

Под устойчивостьюсистемы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие.Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис.61). Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы.Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

В соответствии с классическим методом решение дифференциального уравнения ищется в виде:

y(t) = y_вын(t) + y_св(t).

Здесь yсв(t) - общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью:

a_oy⁽ⁿ⁾ + a₁y^(n-1) + ... + a_(n-1)y’ + a_(n)y = 0.

Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y_вын(t) - частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействиеu(t). Поэтому вторая составляющая общего решения называетсявынужденный. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

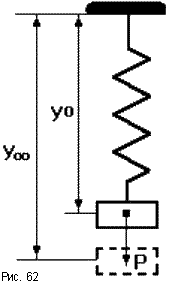Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времениt = 0подвесить к пружине груз, то на свободные колебания наложится внешняя силаР. После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющейy_вын = y(t ). Если внешнее воздействие само будет изменяться по синусоидальному законуP = P_osin(t +), то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то естьy_вын = y_maxsin(t + y).

Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t . Свободная составляющая представляет собой сумму из n отдельных составляющих: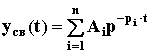, гдеp_i корни характеристического уравненияD(p) = a₀p_n + a₁p_n-1 + a₂p_n-2 + ... + a_n = 0. Корни могут быть либо вещественными p_i = a_i, либо попарно комплексно сопряженнымиp_i = a_i ± ji. Постоянные интегрированияА_i определяются исходя из начальных и конечных условий, подставляя в общее решение значенияu, yи их производные в моменты времени t = 0и t .

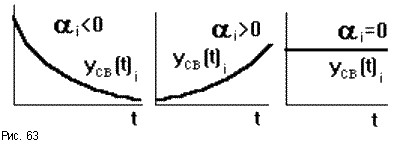
Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y_св(t)_i, каждому положительному - экспоненциально расходящаяся, каждому нулевому корню соответствуетy_св(t)_i = const(рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой_i, при положительной вещественной части - расходящиеся колебания, при нулевой - незатухающие (рис.64).

Так как после снятия возмущения y_вын(t) = 0, то устойчивость системы определяется только характером свободной составляющейy_св(t). zПоэтомуусловие устойчивости систем по Ляпуновуформулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.

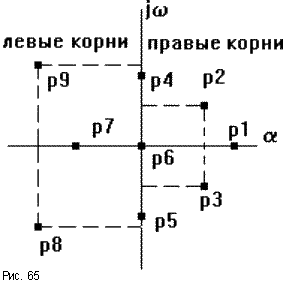
Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми, с положительными -правыми (рис.65).

Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a_n = 0), а остальные левые, то система находится награнице апериодической устойчивости. Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится награнице колебательной устойчивости.

Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости. Их можно разделить наалгебраические(основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) ичастотные(основаны на исследовании частотных характеристик).