ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 401
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
Лекция 9.Частотные критерии устойчивости
Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинствов простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.
9.1. Принцип аргумента
Запишем характеристический полином САУ в виде
D(p) =
a0
(p
- p1)
(p
- p2)
...
(p
- pn)
= 0.
Его корни
pi
=
i
+ j
i
= |pi|ejarg(pi),
где
arg(pi)
= arctg(
i/ai)
+ k
,
.
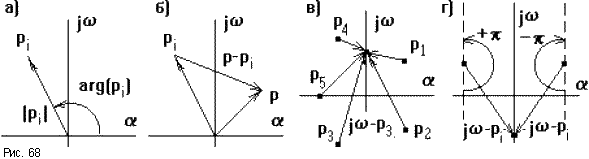
Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - piизобразится разностью векторов (рис.68б), гдеp - любое число.
Еcли менять значение p произвольным образом, то конец вектора p - piбудет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так какpi- это конкретное неизменное значение.
В частном случае,
если на вход системы подавать гармонические
колебания с различной частотой
,
тоp = j
,
а характеристический полином принимает
вид:
D(j
)
= a0
(j
- p1)
(j
- p2)
...
(j
- pn).
При этом концы
векторов j
- piбудут
находиться на мнимой оси (рис.68в). Если
менять
от-
до+
,
то каждый векторj
- pi
будет поворачиваться относительно
своего началаpiна угол +pдля левых и- pдля правых
корней (рис.68г).
Характеристический полином можно представить в виде
D(j
)
= |D(j
)|ejarg(D(j
)),
где
|D(j
)|
= a0
|j
- p1|
|j
- p2|...|j
- pn|,
arg(D(j
))
= arg(j
- p1)
+ arg(j
- p2)
+ .. + arg(j
- pn).
Пусть из n корнейm- правые, аn - m- левые, тогда
угол поворота вектораD(j
)при изменении
от-
до
+
равен
=
(n - m)
- m
,
или при изменении
от0до +
получаем
=
(n - 2m)
(
/2).
Отсюда вытекает
правило: изменение аргумента вектора
b при изменении частоты
от
-
до
+
равно разности между числом левых и
правых корней уравненияD(p) = 0,
умноженному на
,
а при изменении частоты
от0до +
эта разность умножается на
/2.
Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
9.2. Критерий устойчивости Михайлова
Так как для
устойчивой САУ число правых корней m
= 0, то угол поворота вектораD(j
)составит
=
n
/2.
То есть САУ будет
устойчива, если вектор D(j
)при изменении частоты
от
0 до +
повернется
на уголn
/2.
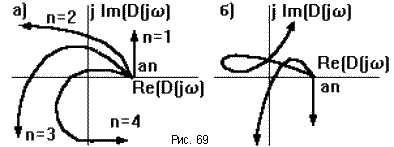
При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так какD(0) = an, и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность вn- ом квадранте (рис.69а).
Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов (рис.69б)), то такая САУ неустойчива - это и естьнеобходимое и достаточное условие критерия Михайлова.
Достоинства. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.
Для облегчения
построения годографа Михайлова выражение
для D(j
)представляют суммой вещественной и
мнимой составляющих:
D(j
)
= a0(j
- p1)(j
- p2)...(j
- pn)
= a0(j
)n
+ a1(j
)n
- 1 + ... + an
= ReD(j
)
+ jImD(j
),
где
ReD(j
)
= an
- an
- 2
2
+ an-
4
4
- ...,
ImD(j
)
= an
- 1
- an
- 3
3
+ an-
5
5
- ....
Меняя
от0до
по
этим формулам находят координаты точек
годографа, которые соединяют плавной
линией.