ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 448
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
Зная передаточную
функцию W(p) = K(p)/D(p), выражение для
переходной функции можно найти из
формулы Хевисайда: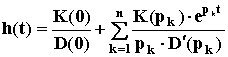 ,
гдеpk- корни характеристического уравненияD(p) = 0. Взяв производную от переходной
функции можно получить выражение для
импульсной переходной функции
,
гдеpk- корни характеристического уравненияD(p) = 0. Взяв производную от переходной
функции можно получить выражение для
импульсной переходной функции
![]() (t)
= h’(t).
(t)
= h’(t).
5.2. Переходные характеристики элементарных звеньев
Здесь мы рассмотрим только самые основные звенья.
5.2.1. Безынерционное (пропорциональное, усилительное) звено
Это звено, для которого в любой момент времени выходная величина пропорциональна входной.
Его уравнение:
y(t) = k![]() u(t).
u(t).
Передаточная функция: W(p) = k.
Переходная
характеристика: h(t) = k![]() 1(t).
1(t).
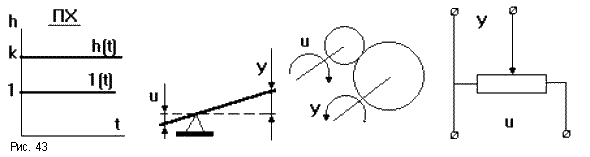
В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в kраз большей, чем на входе и сохраняет это значение (рис.43). Приk = 1звено никак себя не проявляет, а при k = - 1- инвертирует входной сигнал.
Любое реальное звено обладает инерционностью, но с определенной точностью некоторые реальные звенья могут рассматриваться как безынерционные, например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель и т.п.
5.2.2. Интегрирующее (астатическое) звено
Его уравнение
![]() ,
или
,
или![]() ,
илиpy = ku.
,
илиpy = ku.
Передаточная функция: W(p) = k/p.
Переходная
характеристика:
![]() (рис.44).
(рис.44).
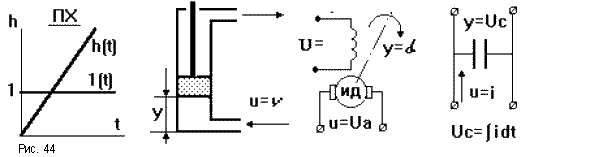
При k = 1звено представляет собой “чистый” интеграторW(p) = 1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие. Примеры интегрирующих звеньев: электродвигатель, поршневой гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему в астатическую, то есть ликвидирует статическую ошибку.
5.2.3. Инерционное звено первого порядка (апериодическое)
Уравнение динамики:
![]() ,
илиTpy + y = ku.
,
илиTpy + y = ku.
Передаточная
функция: W(p) =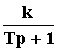 .
.
Переходная характеристика может быть получена с помощью формулы Хевисайда:
 ,
,
где p1 = - 1/T- корень уравненияD(p) = Tp + 1 = 0; D’(p1) = T.
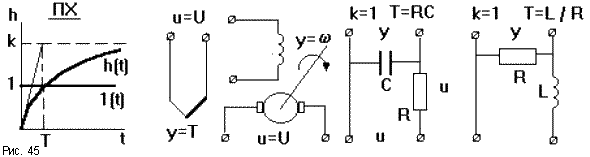
Переходная характеристика имеет вид экспоненты (рис.45), по которой можно определить передаточный коэффициент k, равный установившемуся значению h(t), и постоянную времениТпо времениt, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно большихТзвено на начальном участке может рассматриваться как интегрирующее, при малыхТзвено приближенно можно рассматривать как безынерционное. Примеры апериодического звена: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.
5.2.4. Инерционные звенья второго порядка
Его уравнение: T12p2y + T2py + y = ku.
Передаточная
функция: W(p) =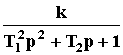 .
.
Решение уравнения
зависит от соотношения постоянных
времени T1иT2,
которое определяет коэффициент затухания
r =![]() .
Можно записатьW(p) =
.
Можно записатьW(p) =
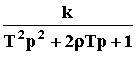 ,
гдеT = T1.
,
гдеT = T1.
Если r![]() 1, то знаменательW(p)имеет два
вещественных корняp1иp2и раскладывается на два сомножителя:
1, то знаменательW(p)имеет два
вещественных корняp1иp2и раскладывается на два сомножителя:
T2p2
+ 2rTp + 1 = T2![]() (p
- p1).(p
- p2).
(p
- p1).(p
- p2).
Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.
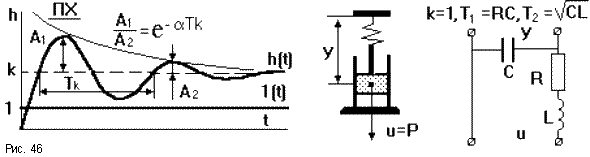
При r<1корни
полинома знаменателяW(p)комплексно
сопряженные:p1,2
=
![]() ±
j
±
j![]() .
Переходная характеристика представляет
собой выражение, характеризующее
затухающий колебательный процесс с
затуханием
.
Переходная характеристика представляет
собой выражение, характеризующее
затухающий колебательный процесс с
затуханием
![]() и
частотой
и
частотой
![]() (рис.46).
Такое звено называетсяколебательным.
Приr = 0колебания носят незатухающий
характер. Такое звено является частным
случаем колебательного звена и называетсяконсервативным. Примерами
колебательного звена могут служить
пружина, имеющая успокоительное
устройство, электрический колебательный
контур с активным сопротивлением и т.п.
Зная характеристики реального устройства
можно определить его параметры как
колебательного звена. Передаточный
коэффициент kравен установившемуся
значению переходной функции.
(рис.46).
Такое звено называетсяколебательным.
Приr = 0колебания носят незатухающий
характер. Такое звено является частным
случаем колебательного звена и называетсяконсервативным. Примерами
колебательного звена могут служить
пружина, имеющая успокоительное
устройство, электрический колебательный
контур с активным сопротивлением и т.п.
Зная характеристики реального устройства
можно определить его параметры как
колебательного звена. Передаточный
коэффициент kравен установившемуся
значению переходной функции.
5.2.5. Дифференцирующее звено
Различают идеальное
и реальное дифференцирующие звенья.
Уравнение динамики идеального звена:
y(t) =
![]() ,
илиy = kpu. Здесь выходная величина
пропорциональна скорости изменения
входной величины. Передаточная функция:W(p) = kp. Приk = 1звено осуществляет
чистое дифференцированиеW(p) = p.
Переходная характеристика: h(t) = k
,
илиy = kpu. Здесь выходная величина
пропорциональна скорости изменения
входной величины. Передаточная функция:W(p) = kp. Приk = 1звено осуществляет
чистое дифференцированиеW(p) = p.
Переходная характеристика: h(t) = k![]() 1’(t)
= d(t).
1’(t)
= d(t).
Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.
Его уравнение: Tpy + y = kTpu.
Передаточная
функция: W(p) =
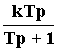 .
.
При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики можно вывести с помощью формулы Хевисайда:
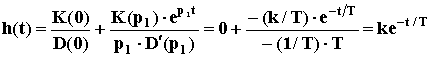 ,
,
здесь p1 = - 1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того,D’(p1) = T.
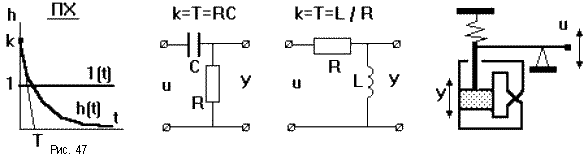
При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени (рис.47). По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициент kи постоянную времениТ. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.
Кроме рассмотренных
имеется еще ряд звеньев, на которых
подробно останавливаться не будем. К
ним можно отнести идеальное форсирующее
звено (W(p) = Tp + 1, практически не
реализуемо), реальное форсирующее звено(W(p) =
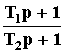 ,
приT1 >>
T2),
запаздывающее звено (W(p) = e -
pT),
воспроизводящее входное воздействие
с запаздыванием по времени и другие.
,
приT1 >>
T2),
запаздывающее звено (W(p) = e -
pT),
воспроизводящее входное воздействие
с запаздыванием по времени и другие.
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
Если подать на вход системы с передаточной функцией W(p) гармонический сигнал
![]()
то после завершения переходного процесса на выходе установится гармонические колебания
![]()
с той же частотой
![]() ,
но иными амплитудой и фазой, зависящими
от частоты
,
но иными амплитудой и фазой, зависящими
от частоты
![]() возмущающего
воздействия. По ним можно судить о
динамических свойствах системы.
Зависимости, связывающие амплитуду и
фазу выходного сигнала с частотой
входного сигнала, называютсячастотными
характеристиками(ЧХ). Анализ ЧХ
системы с целью исследования ее
динамических свойств называетсячастотным анализом.
возмущающего
воздействия. По ним можно судить о
динамических свойствах системы.
Зависимости, связывающие амплитуду и
фазу выходного сигнала с частотой
входного сигнала, называютсячастотными
характеристиками(ЧХ). Анализ ЧХ
системы с целью исследования ее
динамических свойств называетсячастотным анализом.
Подставим выражения для u(t)иy(t)в уравнение динамики
(aоpn + a1pn - 1 + a2pn - 2 + ... + an)y = (bоpm + b1pm-1 + ... + bm)u.
Учтем, что
![]()
а значит
pnu = pnUmejwt = Um (jw)nejwt = (jw)nu.
Аналогичные соотношения можно записать и для левой части уравнения. Получим:
![]()
По аналогии с передаточной функцией можно записать:
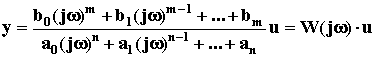 .
.
W(j![]() ),
равная отношению выходного сигнала к
входному при изменении входного сигнала
по гармоническому закону, называетсячастотной передаточной функцией.
Легко заметить, что она может быть
получена путем простой замены p на j
),
равная отношению выходного сигнала к
входному при изменении входного сигнала
по гармоническому закону, называетсячастотной передаточной функцией.
Легко заметить, что она может быть
получена путем простой замены p на j![]() в выражении W(p).
в выражении W(p).
W(j![]() )
есть комплексная функция, поэтому:
)
есть комплексная функция, поэтому: