Файл: kurs-lekcij-po-tau.doc

3.Перерегулирование- это максимальное отклонение управляемой величины от установившегося значения, выраженное в относительных единицах: 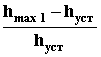 =. Здесьh_max1- значение первого максимума переходной характеристики. При больших перерегулированиях могут возникнуть значительные динамические усилия в механической части системы, электрические перенапряжения и т.п. Допустимое значениеs определяется из опыта эксплуатации. обычно оно составляет 0.1...0.3, иногда допускается до 0.7.

4.Частота колебаний = 2/T, где T- период колебаний.

5.Число колебаний nза времяt_пп.

6. Декремент затуханияk, равный отношению двух смежных перерегулирований:.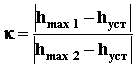

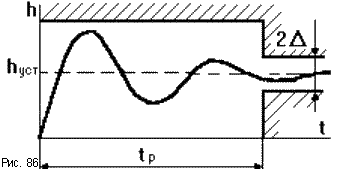
При создании САУ допустимые значения показателей качества оговариваются техническими условиями, что можно представить в виде диаграммы показателей качества. Это область, за границы которой не должна выходить переходная характеристика (рис.86).

11.3.2. Оценка качества управления при периодических возмущениях

Периодические возмущения можно разложить в ряд Фурье, поэтому их воздействие удобно анализировать по частотным характеристикам, показывающим, как звено преобразует гармонический сигнал.

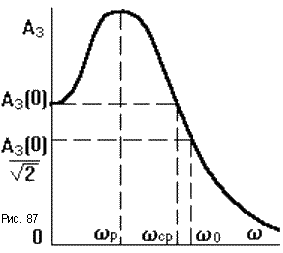
Обычно используют АЧХ замкнутой САУ (рис.87), которую легко построить по АФЧХ разомкнутой САУ W_p(j), по формуле

Aз = .

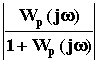По этой кривой можно получить ряд показателей качества.

1.Показатель колебательностиM- это отношение максимального значения АЧХ замкнутой САУ к ее значению при = 0, то естьM = A_зmax()/Aз(0). Так как

Aз(0) =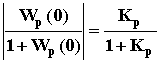1,

при K_p >> 1, то M A_зmax(). Он характеризует склонность системы к колебаниям и не должен превышать 1.5.

2. Резонансная частота системы _p- это частота, при которой колебания проходят через систему с наибольшим усилением, а АЧХ достигает максимума.

3.Полоса пропускания системы - это интервал частот от = 0до= ₀, на котором выполняется условиеAз(₀)0.707. Если она высокая, то система будет воспроизводить высокочастотные помехи.

4.Частота среза _ср- при которой АЧХ замкнутой САУ принимает значение, равное единице. По ней можно судить о длительности переходного процессаt_пп(1..2)2/_ср.

5.Склонность САУ к колебаниям характеризуют также ее запасы устойчивости по модулю (допускается от 6 до 20дб) и по фазе (допускается от 30 до 60 градусов).

Лекция 12.Корневой и интегральный методы оценки качества сау

12.1. Корневой метод оценки качества управления

Это косвенный метод, основанный на определении границ области расположения корней характеристического уравнения на комплексной плоскости, что дает возможность приблизительно оценить качество управления.

Пусть имеется дифференциальное уравнение замкнутой САУ:

 (a₀pⁿ + a₁p^n-1 + a₂p^n-2 + ... + (a_n)y = (b₀p^m + b₁p^m-1 + ... + b_m)u.

Передаточная функция САУ

,

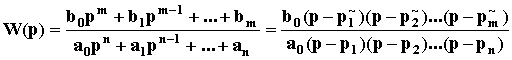где p~¹,p~²,...,p~^m- нули передаточной функции,p¹,p²,...,pⁿ- полюса передаточной функции.

 Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ. Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей:

.

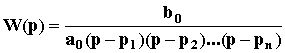Тогда уравнение динамики приобретает вид:

(a₀pⁿ + a₁p^n-1 + a₂p^n-2 + ... + a_n)y = b₀u.

Общее решение данного уравнения имеет вид:

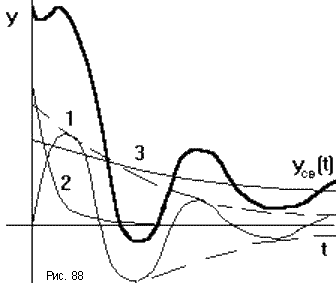
y(t) = y^св + y^вын = åA_ie^pit + bо/a_n.

Время переходного процесса t^ппопределяется длительностью свободного процесса, который представляет собой суммуnэкспоненциально затухающих составляющих (рис.88). Затухание каждой из составляющих определяется вещественной частью соответствующего плюса pi, которая для устойчивых систем должна быть отрицательна. Длительность переходного процесса определяется в основном свободной составляющей, имеющей наименьшее затухание, то есть наименьшее абсолютное значение вещественной части соответствующего полюса.

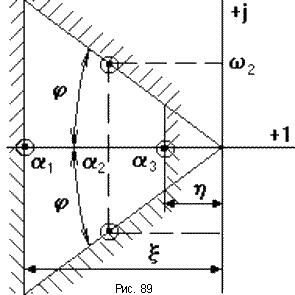
Если изобразить все полюса в комплексной плоскости корней (рис.89), то данный полюс (или пара комплексно сопряженных полюсов) будет наиболее близко расположен к мнимой оси.

Для приблизительной оценки качества САУ на плоскости корней выделяется область в виде трапеции, на сторонах которой находится хотя бы по одному корню, все остальные корни - внутри данной области. Эта область характеризуется параметрами: h-степень устойчивости(равна расстоянию от мнимой оси до ближайшего корня или пары комплексно сопряженных корней); m = tg(j)-колебательность(характеризует колебательность переходного процесса и величину перерегулирования); x- своего названия не имеет, равна вещественной части наиболее удаленного от мнимой оси корня.

По степени устойчивости hможно приблизительно вычислить время переходного процесса, которое определяется по моменту, когда свободная составляющая с наименьшим затуханием уменьшится до величины A_i , гдеA_i- начальное значение данной составляющей, то на рис.84:

y^св₃(t) = A₃ =A₃ = > .

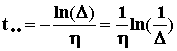В общем случае, когда передаточная функция замкнутой САУ имеет нули, то использование данного метода может дать большую ошибку. Однако всегда качество управления будет тем лучше, чем больше hи меньшеm, поэтому данный метод имеет смысл для любых САУ, но приближенно.

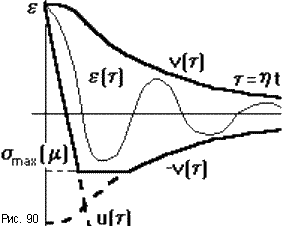
Зная значения h, x, mможно оценить область, за которую кривая переходного процесса выходить не будет (рис.90). Для этого строятся две кривые:u(t,h)- миноранта иv(t,h)- мажоранта, ограничивающая кривую переходного процесса соответственно снизу и сверху так, чтоu(t,h)e(t)v(t,h), гдеe(t) = y_o-y(t). Формулы для определения миноранты и мажоранты берутся в справочниках для конкретных случаев.