Файл: Методичка по механике вся Печать новый вариант12г.doc

Замечание. Возможность движения по поверхности при наличии силы трения обусловлена ее ограниченностью по величине. Чем меньше коэффициент трения (зависящий от качества покрытия, шероховатости соприкасающихся поверхностей), тем меньшее сопротивление испытывает движение.

Методические указания. Нами рассмотрены естественно не все силы. В задачах могут встретиться просто заданные внешние силы без указания их источников, например, сила тяги, приложенная сила и пр. Сила задана, если известны не только ее направление и величина, но и также точка ее приложения (указано тело, на которое она действует). Если в условии задачи говорится о действующих силах или заданы какие-либо параметры, относящиеся к величине некоторой силы, то значит это – задача на динамику и решать ее надо на основе второго закона Ньютона – единственного равенства, привносящего в формулу силы.

Алгоритм решения задач по динамике.

1. Выбрать тело, о котором идет речь в условии задачи.

2. Указать на рисунке все силы, действующие на это тело (в виде векторов с соответствующими обозначениями).

3. Выяснить есть ли у этого тела ускорение и изобразить (если возможно) его направление на рисунке (по крайней мере должна быть известна линия вдоль которой направлено это ускорение, если нельзя точно заранее сказать в какую именно сторону).

4. Ответить на вопросы: движется ли тело с ускорением? Какая сила (или силы) сообщает телу это ускорение? Выбрать форму записи второго закона Ньютона (1-я, 2-я или 3-я, см. методические указания на с.46).

5. Записать в векторной форме формулу (2.2) второго закона Ньютона.

6. Выбрать и нарисовать оси координат (только их направления), на которые далее спроецировать записанное векторное равенство.

7. Полученные таким образом скалярные равенства дополнить при необходимости формулами кинематических зависимостей и выразить из них искомую величину.

8. Возможно рассмотрение в переделах одной задачи нескольких тел (при недостатке одного равенства для сил), тогда все предыдущие этапы будут повторяться несколько раз.

9. Проверить согласование причин и характера изменения движения рассмотренных тел. Сделать анализ полученных результатов, ответить на поставленный в задаче вопрос.

Примеры решения задач

Задача-пример 1. На тележке массой 20 кг лежит груз массой 5 кг. К грузу приложена сила F, сообщающая тележке с грузом ускорение а. Сила действует под углом 30⁰ к горизонту. Каково максимальное значение этой силы, при котором груз не будет скользить по тележке? Коэффициент трения между грузом и тележкой 0,20. Трением между тележкой и дорогой пренебречь. С каким ускорением будет двигаться тележка под действием силы F?

П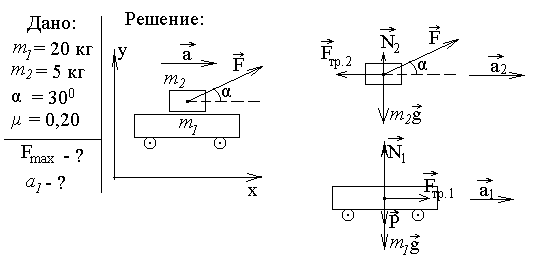режде всего, по условию задачи сделаем рисунок, указав на нем некоторые данные и искомые величины.

Далее необходимо проанализировать заданную ситуацию. Ясно, что в задаче рассматривается движение двух тел: груза и тележки. Причем возможны два варианта их движения: 1) оба тела движутся вместе, тогда ускорения их равны ; 2) тела движутся по-разному, т.е. груз скользит по тележке и его ускорение больше по величине, т.е.а₁ < а₂. Но в обоих случаях тела движутся с ускорениями. Ответим на вопрос о том, какая сила сообщает каждому из рассматриваемых тел это ускорение.

Для этого необходимо указать все силы, действующие отдельно на груз и на тележку, и выбрать те из них, которые имеют направление (или составляющую) вдоль направления ускорения. Итак, груз приобретает ускорение под действием двух сил (приложенной к нему внешней силы и силы трения). Второй закон Ньютона для него запишется в форме 2 (см. методические указания на с.46) для проекций сил:

,

находим эти проекции на направление ускорения и получаем скалярное равенство в виде:

m₂  а₂ = Fcos – F_тр2 (1).

С другой стороны, в направлении вертикальной оси движение груза не меняется, а значит силы, действующие вдольнего, скомпенсированы, т.е.сумма проекцийэтих сил на данное направление равна нулю:

или

Fsin + N₂ – m₂g = 0 (2).

Методическое указание. Приведенная логика рассуждений отличается от общепринятого универсального способа тем, что при рассмотрении выбранного направления заранее отбрасываются силы, имеющие на него нулевые проекции. Более общая логика состоит в записи второго закона в форме 3 и последующем проектировании его на нужные направления. Автор ни сколько не умаляет достоинств таких действий (простота в использовании, универсальность и пр.), но предостерегает от привычки действовать «по шаблону», не вникая в физические взаимосвязи и не проявляя гибкости мышления! Приводимые в качестве примера рассуждения демонстрируют взаимосвязь теории с практикой, т.е. раскрывают сущность сил, как причин изменения движения тел.

Таким образом, получены два равенства из рассмотрения движения груза. Перейдем теперь к тележке. Под действием какой силы тележка движется с ускорением???

Как видно из рисунка, где указаны все действующие на нее силы, такой силой является сила трения.

Методическое указание. Важно обратить особое внимание на двоякую роль силы трения при движении: 1-я – оказывает сопротивление движению (помеха) и 2-я – оказывается причиной (источник) движения. Поэтому каждый раз необходимо заново анализировать ситуацию с целью распознать, какова же роль трения в этом случае.

Учитывая третий закон Ньютона, приходим к выводу, что F_тр.2 = F_тр.1 = F_тр.(методическое требование:равные по модулю величины следует обозначать одинаково!). Второй закон Ньютона для тележки запишем в форме 1:

,

вектор справа равен вектору слева, значит равны модули этих векторов и можно опустить значки вектора: m₁ a₁ = F_тр.1(3).

Методическое указание. Определять силу N чаще всего приходится с целью последующего нахождения значения силы трения скольжения. Поэтому там, где силу трения не учитывают и не требуется специально определить реакцию опоры, вертикальное направление (а значит и вся совокупность сил, действующих в этом направлении) не рассматривается.

В вертикальном направлении на тележку действуют 3 силы: сила реакции дороги, сила тяжести и вес лежащего на ней груза. Заметим, что !

После того, как проделали анализ движения рассмотренных тел, переходим к нахождения искомых величин.

М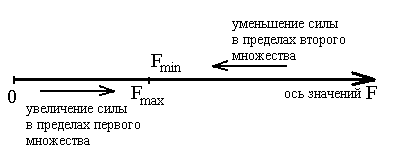етодическое указание. Сложным моментом является понимание диалектики предельных значений. Так, максимальное значение силы F, когда груз все еще не движется по тележке, есть то же самое, что и минимальное значение силы F, когда груз еще движется по тележке. Разница состоит в направлении подхода к данному граничному значению силы. Иначе говоря, значение F_max разбивает всю совокупность возможных значений силы F на два множества: 1) значения, при которых груз не скользит по тележке; 2) значения, при которых груз скользит по тележке. Эти множества не пересекаются (не имеют общих элементов). Каждый элемент первого из них меньше всякого элемента из второго множества (чтобы заставить груз скользит надо очевидно увеличить приложенную силу!). Само же значение F_max находится и в одном и в другом, т.к. является их общей границей. Но когда идет речь о границе первого множества, то граница именуется как F_max, граница второго множества по отношению к остальным его элементам является минимальной величиной и обозначается F_min. Значения F_min и F_max равны. Но когда мы ищем F_min мы находимся к условиях скольжения груза, если же ищем предельное значение в виде F_max, то считаем, что груз не скользит по тележке, а значит они движутся как одно целое с равными по величине ускорениями.

Будем искать максимальное значение силы F_max, при котором груз все еще остается неподвижным относительно тележки (нет скольжения). Тогдаа₁=а₂=аи равенства (1) и (3) запишутся в виде:

m₂  а =Fcos – F_тр(1а).

m₁ a =F_тр(3а).

Складывая их почленно получаем запись второго закона Ньютона для системы «груз-тележка» (как единого целого!) в проекции на ось х:

(m₁ + m₂)  а = Fcos (4).

Анализируя взаимозависимости между величинами, участвующими в этих равенствах, видим, что при увеличении силы Fувеличивается общее ускорение системыа, т.е. увеличивается ускорение, в частности, тележки, а стало быть возрастает сила трения, действующая на тележку (причина ее ускорения). Но этот процесс обрывается по достижении силой трения своего максимального значенияF_тр.ск.при величине внешней силыF = F_max. Тогда учтем сразу, что