Файл: Методичка по механике вся Печать новый вариант12г.doc

Основные понятия и законы

Материальные тела участвуют в различных взаимодействиях, т.е. одни из них действуют на другие и наоборот. В природе нет тел, которые бы не принимали участия хотя бы в одном виде взаимодействий, обусловленных его свойствами.

Абстрактно можно представить себе тело, которое ни с кем не взаимодействует, то есть на которое не оказывается никакого действия со стороны. Такое тело называется свободным.

Движение свободного тела не меняется! Его вид: прямолинейное и равномерное. Оно будет оставаться таковым сколь угодно долго. Если движение тела изменится, значит, оно уже не свободное и на него кто-то подействовал.

Главная суть в том, что для движения причин не нужно, причины есть у изменения движения.

Выделим несколько видов взаимодействий: гравитационное (обусловленное наличием массы), упругое (обусловленное взаимодействием микрочастиц, из которых состоит данное тело), электростатическое (обусловлено наличием у тела электрического заряда) и магнитное (обусловленное движением зарядов). Такая классификация имеет целью подтвердить данное ниже определение основной в динамике физической величины.

Сила –мера взаимодействия; векторная величина, имеющая модуль и направление. Сила всегда действует со стороны одного тела (или системы тел) на другое тело (или систему). Например, сила тяжести – это сила со стороны «Земли» на «данное тело, имеющее массу». В связи с этим будем говорить о всякой силе по следующей схеме:

кто действует – на кого действует – как направлена – чему равна.

Основные силы, рассматриваемые при решении задач, будут описаны ниже, после изучения законов Ньютона, т.к. взаимосвязи между некоторыми из них вытекают из третьего закона Ньютона.

Динамика Ньютона основана на утверждении, что причиной изменения движения тела служит некоторая сила (или несколько сил), подействовавшая на него.Иначе, тело не меняет своего движения при отсутствии внешней действующей на него силы. Если сил несколько, то имеется в виду результирующая сила – векторная сумма всех действующих на тело внешних сил. Причем при отсутствии сил тело не обязано покоится, оно может двигаться, но с постоянной скоростью, т.е. равномерно и прямолинейно. Этоявлениеравномерного и прямолинейного движения тела при отсутствии внешних воздействий называетсяинерцией.

Но для изменения движения материального тела не достаточно только наличия внешней действующей силы! Нужно еще некоторое времяее действия, чтобы это изменение произошло. Т.е. материальное тело изменяет свое движение не мгновенно. Иначе, оно оказывает некоторое сопротивление изменению своего движения.Свойствотел оказывать сопротивление изменению своего движения называетсяинертностью.Для характеристики инертных свойств тел потребовалось ввести новую величину: инертную массу как меру податливости тела внешнему воздействию. Итак,масса– мера инертности тела; скалярная аддитивная положительная величина, зависящая от количества вещества.

Как выяснилось, свойство инерции проявляется не во всех системах отсчета! Например, относительно ускоряющегося поезда пенек на поляне движется ускоренно при отсутствии внешних сил в горизонтальном направлении. Поэтому все системы отсчета делят на инерциальные (относительно которых инерция имеет место) и неинерциальные (в противном случае). Приходим к следующему определению:

Инерциальной системой отсчета называется такая система отсчета, относительно которой тело сохраняет свое состояние покоя или равномерного движения, если на него не действуют внешние силы или их действие скомпенсировано (т.е. результирующая этих сил равна нулю). Такими системами являются системы отсчета, связанные с Землей (в пределах земной поверхности) или с Солнцем (в более широких пределах) и т.д. Кроме того, любая система отсчета, неподвижная или движущаяся равномерно относительно инерциальной, также является инерциальной. Например, перрон или поезд, движущийся с постоянной скоростью. Неинерциальные системы отсчета связанны с телами, которые движутся с ускорением (прямолинейно или по окружности, или по любой кривой линии).

Теперь переходим к формулировке трех законов классической динамики Исаака Ньютона.

Первый закон Ньютона: существуют инерциальные системы отсчета.

Второй закон Ньютона – основной закон поступательного движения – отвечает на вопрос, как изменяется механическое движение тела под действием приложенной силы: (2.1).

Т.е. ускорение, приобретаемое телом под действием силы F прямо пропорционально величине этой силы. Коэффициент пропорциональности при этом есть величина обратная массе тела, а значит ускорение обратно пропорционально массе этого тела.

При решении задач используется более простая форма записи этого закона: (2.2).

Замечание. Однако формулировать закон необходимо в форме (2.1)!

Методические указания. На практике возможны следующие случаи использования этого закона (формы применения второго закона Ньютона):

1. ускорение, с которым движется тело, вызвано только одной силой F, тогда формула (2.2) запишется только для этой силы. При этом справа и слева будут только по одному вектору, поэтому значок вектора можно опустить и переписать формулу сразу в скалярной форме: F = mа, где а – величина ускорения тела, вызванного силой, численно равной F.

2. Ускорение вызвано несколькими силами, направленными вдоль направления ускорения (или имеющими составляющие вдоль этого направления), тогда справа в формуле (2.2) будет записана векторная сумма этих сил (сумма проекций этих сил на направление ускорения). Помимо них могут действовать и еще какие-то силы, которые перпендикулярны рассматриваемому ускорению, а потому не дают вклада в его величину и не учитываются. Затем для получения скалярной записи это равенство проектируется на направление ускорения.

3. Затруднительно или малоэффективно разделение всех действующих сил на те, что привносят вклад в изменение движения, и те, которые компенсируются и потому не изменяют движения. Тогда формула (2.2) запишется в самом общем случае для результирующей всех действующих сил. Т.е. справа надо записывать векторную сумму всех указанных сил (при этом важно не упустить из виду ни одной силы). Далее полученное векторное равенство проектируется на несколько взаимноперпендикулярных направлений (оси координат). Тем самым будет получено более одного скалярного равенства, что важно в случае нескольких неизвестных.

Третий закон Ньютона: Рассматривается взаимодействие двух тел в форме материальных точек. Пусть– сила, действующая на первое тело со стороны второго, и– сила, действующая на второе тело со стороны первого. Тогда: 1)если одно тело действует на второе с некоторой силой, то и второе тело действует на первое с какой-то силой; 2)обе силы взаимодействия направлены вдоль линии, проходящей через данные материальные точки (центральный характер сил); 3) верно векторное равенство(2.3) , т.е. эти силы равны по величине и противоположно направлены.

Методические указания. Иногда кратко этот закон формулируют в виде: сила действия равна силе противодействия. Заметим, что учитывая векторность силы, это совершенно не верно: силы действия и противодействия различны по направлению. Возможно в слове «противо-действие» этот момент и учитывается!? Однако суть закона далеко этим не ограничивается. Основной смыл состоит в том, что действие всегда вызывает противодействие, т.е. является одной из сторон взаимо-действия. Отсюда требование: говоря о силе надо указать о какой стороне взаимодействия идет речь, т.е. действие на какое именно тело нас интересует в данный момент!

В заключение рассмотрения трех основных законом ньютоновской динамики обратим особое внимание на следующее: законы Ньютона справедливы только в инерциальных системах отсчета!

Отсюда важное методическое требование: при решении задач по динамике всегда указывать относительно какой ИСО рассматривается движение или изменение движения (т.е. состояние) тела. Все величины, входящие в формулу (2.2) или (2.1), должны быть заданы относительно ОДНОЙ и ТОЙ ЖЕ системы отсчета.

Теперь рассмотрим основные виды сил, затрагиваемых в задачах по динамике.

Про каждую силу надо знать:

1. Кто действует?

2. На кого действует?

3. Куда направлена?

4. Чему равна?

5. Точка приложения силы (важно в статике!).

6. Природа силы (см. 4 фундаментальных взаимодействия: гравитационное, электромагнитное, сильное и слабое).

1. Сила тяжести 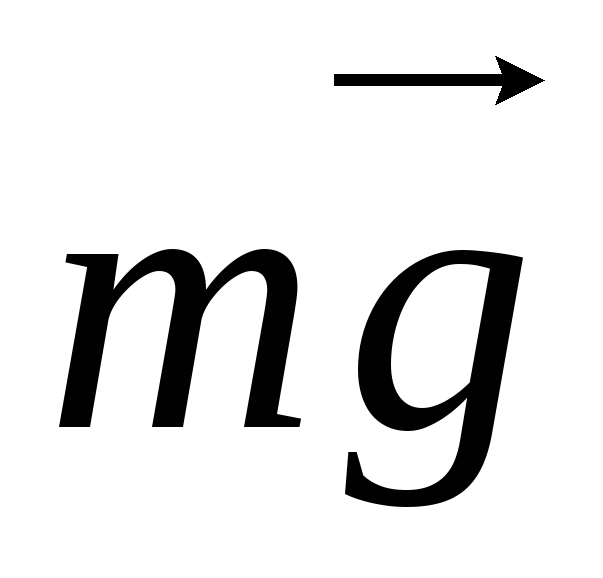. – Земля действует на тело массы m, приложена к центру тяжести и направлена к центру Земли (вдоль радиуса Земли) от данного тела, равна по величине произведениюmg, гдеg– ускорение свободного падения (постоянная величина, равная у поверхности Земли примерно 9,8 м/с²).

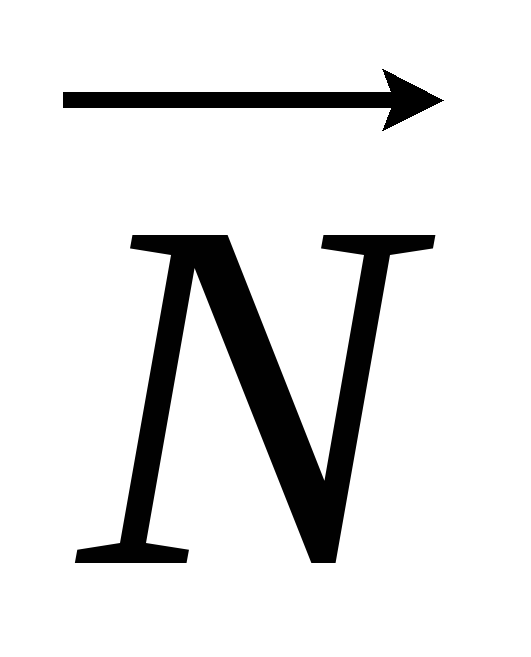2. Сила реакции опоры –опора действует на тело, направлена перпендикулярно опоре от опоры. Величина зависит от конкретных условий; часто равна по модулю весу тела (по третьему закону Ньютона).

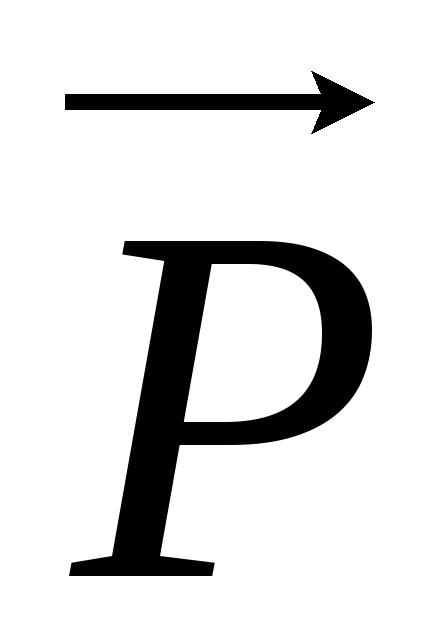3. Вес тела –тело действует на опору или подвес, направлена перпендикулярно к опоре в сторону опоры или вдоль подвеса от точки подвеса. Значение зависит от характера движения опоры (или подвеса). Иначе говоря, весом тела называют силу, с которой тело действует на опору или растягивает подвесвследствие притяжения к Земле, и тогда считают, чтоР = mg(при этом важно помнить, что опора или подвес должны быть неподвижными). Если опора движется вертикально с ускорениема, направленнымвниз или вверх, то модуль веса тела равенР=m(g-a)илиР=m(g+a). В связи с этим важно отметить, что между весом тела и величиной силы тяжести нет однозначной количественной связи!Кроме того, тело может прижиматься к опоре и какой-либо другой внешней силой (например, брусок можно рукой придавить к столу, а груз, висящий на нити может еще и снизу поддерживаться и т.д.), тогда говорят осиле давления груза на опору или о силе, с которой груз действует на подвес.

4. Сила натяжения нити –нить (подвес) действует на прикрепленное к нему тело, направлена вдоль нити от точки подвеса. Модуль этой силы зависит от конкретных условий задачи; лишь иногда равна по величине весу тела.

5. Сила упругости 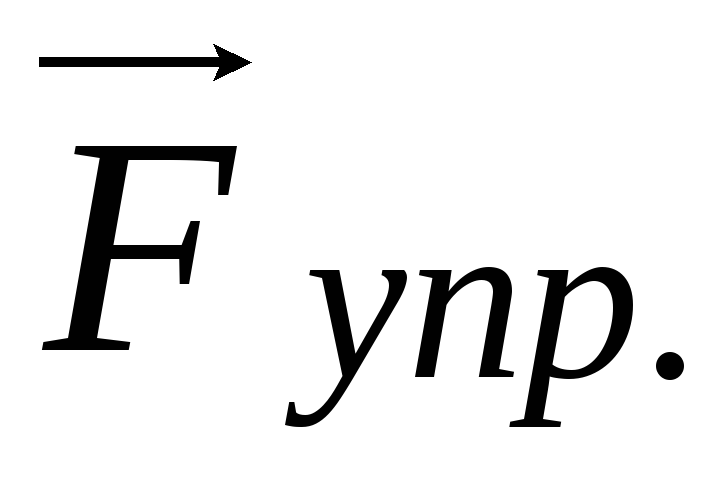– пружина или упругий стержень действует на прикрепленное к ней или к нему тело, направлена вдоль оси деформации (вдоль направления сжатия или растяжения) в сторону уменьшения деформации. Величина определяется законом Гука:F_упр. = kx(2.4), гдех– величина продольной деформации (абсолютное удлинение или сжатиеотносительно недеформированного состояния!).

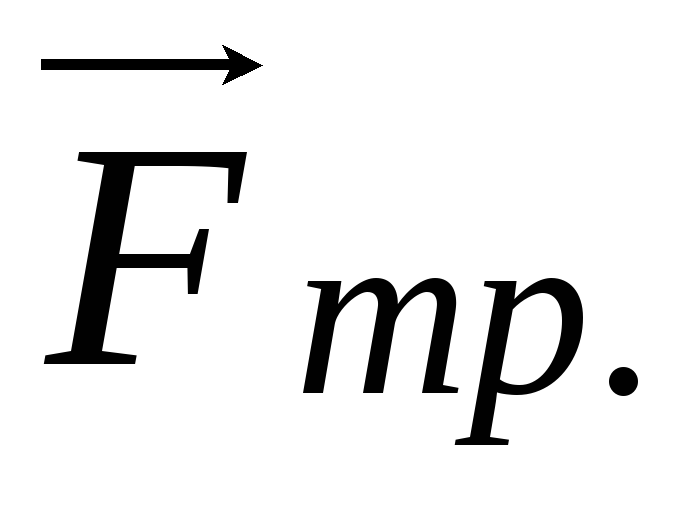6. Сила трения – поверхность действует на находящееся на ней тело, направлена вдоль поверхности в сторону, противоположнуюотносительномудвижению тела (имеется в виду движение действительное или желаемое). По третьему закону Ньютона тело также действует на поверхность с такой же по величине, но противоположной по направлению силой. Если относительное движение равно нулю (нет скольжения), то силу трения называютсилой трения покоя. Ее величина лежит в пределах:0  F_тр.  F_тр.ск., гдеF_тр.ск.– величина силы трения скольжения (она постоянна для данных поверхностей) и равнаF_тр.ск. = N(2.5), гдеN– величина силы нормального давления (перпендикулярная поверхности сила реакции опоры).

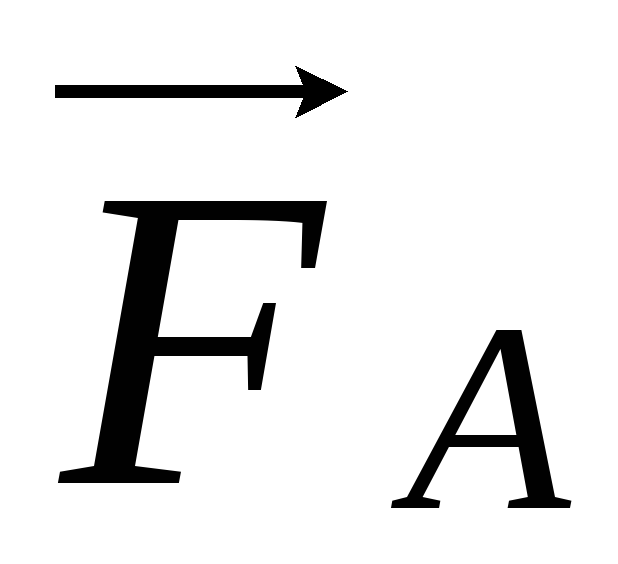7. Сила Архимеда . –вода (газ) действует на погруженное в нее тело, направлена вверх от центра Земли, равна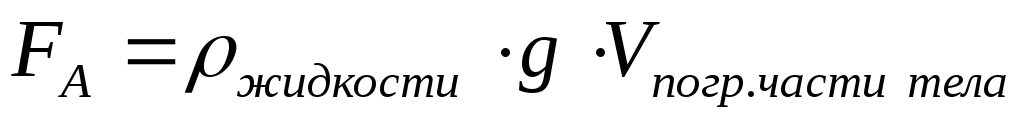.