ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.07.2024
Просмотров: 495
Скачиваний: 0
СОДЕРЖАНИЕ
1.2. Фундаментальные принципы управления
1.2.1. Принцип разомкнутого управления
Лекция 2.Статический режим сау
2.2. Статические характеристики
2.3. Статическое и астатическое регулирование
Лекция 3.Динамический режим сау
3.1. Динамический режим сау. Уравнение динамики
3.2. Линеаризация уравнения динамики
3.4. Элементарные динамические звенья
Лекция 4.Структурные схемы сау
4.1. Эквивалентные преобразования структурных схем
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
5.2.1. Безынерционное (пропорциональное, усилительное) звено
5.2.2. Интегрирующее (астатическое) звено
5.2.3. Инерционное звено первого порядка (апериодическое)
5.2.4. Инерционные звенья второго порядка
Лекция 6.Частотные характеристики
6.1. Понятие частотных характеристик
6.2. Частотные характеристики типовых звеньев
6.2.4. Инерционные звенья второго порядка
6.2.5. Правила построения чх элементарных звеньев
7.1. Частотные характеристики разомкнутых одноконтурных сау
Лекция 8.Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
8.2.1. Необходимое условие устойчивости
Лекция 9.Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. Афчх астатических сау
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по лчх
11.1. Теоретическое обоснование метода d-разбиений
11.3. Прямые методы оценки качества управления
11.3.1. Оценка переходного процесса при ступенчатом воздействии.
11.3.2. Оценка качества управления при периодических возмущениях
Лекция 12.Корневой и интегральный методы оценки качества сау
12.1. Корневой метод оценки качества управления
12.2. Интегральные критерии качества
Лекция 13.Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между вчх и переходной характеристикой
14.1.1. Включение корректирующих устройств
14.1.2. Синтез корректирующих устройств.
14.2. Коррекция свойств сау изменением параметров звеньев
14.2.1. Изменение коэффициента передачи
14.2.2. Изменение постоянной времени звена сау
Лекция 15.Включение корректирующих звеньев
15.1. Коррекция свойств сау включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую сау
15.1.2. Включение апериодического звена
15.1.3. Включение форсирующего звена
15.1.4. Включение звена со сложной передаточной функцией
15.2. Последовательная коррекция по задающему воздействию
Аналогично можно
разложить и функцию нескольких переменных.
Для простоты возьмем упрощенный, но
наиболее характерный вариант уравнения
динамики САУ: F(y,y',y",u,u')
= f. Здесь
производные по времени u',y',y"
также являются переменными. В точке,
близкой к номинальному режиму: f
= fн
+
![]() fи F
= Fн
+
fи F
= Fн
+
![]() F.
Разложим функцию F
в ряд Тейлора в окрестности точки
номинального режима, отбрасывая члены
ряда высоких порядков малости:
F.
Разложим функцию F
в ряд Тейлора в окрестности точки
номинального режима, отбрасывая члены
ряда высоких порядков малости:
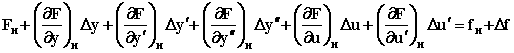 .
.
В номинальном режиме, когда все отклонения и их производные по времени равны нулю, получаем частное решение уравнения: Fн = fн. Учитывая это и вводя обозначения получим:
ao![]() y”
+ a1
y”
+ a1![]() y’
+ a2
y’
+ a2![]() y
= bo
y
= bo![]() u’
+ b1
u’
+ b1![]() u
+ co
u
+ co![]() f.
f.
Отбрасывая все
знаки
![]() ,
получим:
,
получим:
aoy” + a1y’ + a2y = bou’ + b1u + cof.
Отбрасывая все
знаки
![]() ,
получим:
,
получим:
В более общем случае:
aoy(n) + a1y(n-1) + ... + an - 1y’ + any = bou(m) + ... + bm - 1u’ + bmu + cof.
При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения величин y, u, f их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях.
К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:
aoy(n) + a1y(n-1) + ... + an - 1y’ + any = bou(m) + ... + bm - 1u’ + bmu.
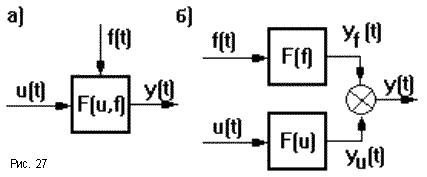
Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п.
Обычно n
![]() m,
так как при n
< m САУ
технически нереализуемы.
m,
так как при n
< m САУ
технически нереализуемы.
3.3. Передаточная функция
В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py, а pn = dn/dtn. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:
aop(n)y + a1p(n-1)y + ... + any = (aop(n) + a1p(n-1) + ... + an)y = (bop(m) + b1p(m-1) + ... + bm)u
Не надо путать эту
форму записи с операционным исчислением
хотя бы потому, что здесь используются
непосредственно функции времени y(t),
u(t) (оригиналы),
а не их изображения
Y(p), U(p),
получаемые из оригиналов по формуле
преобразования Лапласа. Вместе с тем
при нулевых начальных условиях с
точностью до обозначений записи
действительно очень похожи. Это сходство
лежит в природе дифференциальных
уравнений. Поэтому некоторые правила
операционного исчисления применимы к
операторной форме записи уравнения
динамики. Так оператор p
можно рассматривать в качестве сомножителя
без права перестановки, то есть py![]() yp.
Его можно выносить за скобки и т.п.
yp.
Его можно выносить за скобки и т.п.
Поэтому уравнение динамики можно записать также в виде:
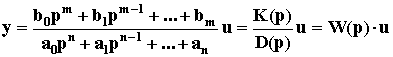
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = bm/an.
Знаменатель передаточной функции D(p) = aopn + a1pn - 1 + a2pn - 2 + ... + an называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции.
Числитель K(p) = bopm + b1pm - 1+ ... + bm называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции.
Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция Wи(p) = 1/p. Схема САУ, составленная из динамических звеньев, называется структурной.
3.4. Элементарные динамические звенья
Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени:
Wэ(p)
=
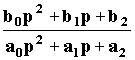 .
.
Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета модно записать
D(p) = aopn + a1pn - 1 + a2pn - 2 + ... + an = ao(p - p1)(p - p2)...(p - pn),
где p1, p2, ..., pn - корни полинома D(p). Аналогично
K(p) = bopm + b1pm - 1+ ... + bm = bo(p - p~1)(p - p~2)...(p - p~m),
где p~1, p~2, ..., p~m - корни полинома K(p). То есть
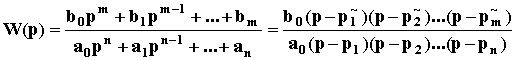
Корни любого
полинома могут быть либо вещественными
pi
= ai
, либо
комплексными попарно сопряженными pi
= ai
± j![]() i
. Любому
вещественному корню при разложении
полинома соответствует сомножитель (p
- ai
).
Любая пара комплексно сопряженных
корней соответствует полиному второй
степени, так как
i
. Любому
вещественному корню при разложении
полинома соответствует сомножитель (p
- ai
).
Любая пара комплексно сопряженных
корней соответствует полиному второй
степени, так как
(p - ai
+
j![]() i
)(p
- ai
-
j
i
)(p
- ai
-
j![]() i
)
= (p - ai)2
+
i
)
= (p - ai)2
+
![]() i
2
= p2
- 2pai
+
(ai
2
+
i
2
= p2
- 2pai
+
(ai
2
+
![]() i
2).
i
2).
То есть
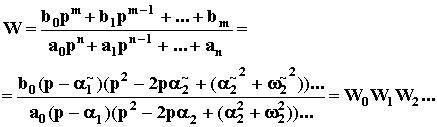
Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой - то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.
В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции которых имеют числитель или знаменатель, равный единице, то есть
W(p) =
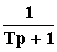 ,W(p) =
,W(p) =
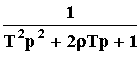 ,
,
W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k.
Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.