ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 364
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
Задания для практических занятий.
№44. Частный предприниматель должен сделать закупку товара (зонтов и солнцезащитных очков) на сумму 70 тыс. руб. Прибыль предпринимателя зависит от выбранной им стратегии и преобладающей погоды и задана платежной матрицей:
|
Товар Погода |
солнце |
дождь |
|
зонты |
-1 |
2 |
|
солнцезащитные очки |
1 |
-2 |
На какую сумму предприниматель закупит каждого товара?
Ответ: Предприниматель потратит по 35 тыс. руб. на зонты и солнцезащитные очки.
№45. Фермер распределяет посевную площадь 70 га между двумя культурами (засухоустойчивой и влагоустойчивой). Прогноз на лето не определен (лето может быть либо засушливым, либо дождливым). Прибыль фермера зависит от выбранной им стратегии и преобладающей погоды летом и задана платежной матрицей:
|
Культура Лето |
засушливое |
дождливое |
|
засухоустойчивая |
1 |
-3 |
|
влагоустойчивая |
-2 |
1 |
Найти распределение площади между культурами, оптимальное для фермера.
Ответ: Оптимальным для фермера будет занять 30 га посевной площади под засухоустойчивую культуру и 40 га – под влагоустойчивую.
Задания для самостоятельного решения.
№46. Предприятие может выпускать три вида продукции (A1, A2, A3), получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний (B1, B2, B3, B4). Дана матрица, элементы которой характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м состоянием спроса.
|
А В |
B1 |
B2 |
B3 |
B4 |
|
A1 |
3 |
3 |
6 |
8 |
|
A2 |
9 |
10 |
4 |
2 |
|
A3 |
7 |
7 |
5 |
4 |
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
№47.
Найти наилучшую стратегию по критерию
Лапласа, Вальда, Сэвиджа, Гурвица для
игры, заданной платежной матрицей:
 .
.
№48.
Найти наилучшую стратегию по критерию
Лапласа, Вальда, Сэвиджа, Гурвица для
игры, заданной платежной матрицей:
 .
.
Равновесие Нэша.
Задания для практических занятий.
№49.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Ответ:
![]() и
и![]() - чистые стратегии;
- чистые стратегии;![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В.
- смешанные стратегии игрока В.
№50.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В.
- смешанные стратегии игрока В.
№51.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В.
- смешанные стратегии игрока В.
№52.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Ответ:
![]() и
и![]() - чистые стратегии;
- чистые стратегии;![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В.
- смешанные стратегии игрока В.
№53.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Ответ:
![]() и
и![]() - чистые стратегии;
- чистые стратегии;![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В.
- смешанные стратегии игрока В.
Задания для самостоятельного решения.
№54.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
№55.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
№56.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
№57.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
№58.
Найти равновесие по Нэшу в чистых, или
в смешанных стратегиях в биматричной
игре:
![]() .
.
№59.
Найти равновесие по Нэшу либо в чистых,
либо в смешанных стратегиях в биматричной
игре:
![]() .
.
Кооперативные решения
№60. В некотором районе имеется три предприятия, каждое из которых нуждается в проводке теплоцентралей. Предприятия могут провести теплоцентрали отдельно друг от друга, а могут объединиться в группы – коалиции. Если предприятие i=1.2.3 прокладывает централь самостоятельно, то затраты составят 100, 200, 300 единиц соответственно. Если 1-е и 2- предприятие объединяться, то их общие затраты составят 250 единиц. Если 1-е и 3-е объединяться, то затраты составят 350 единиц. Если 2-е и 3-е объединятся, то затраты составят 460 единиц. Если все три предприятия объединяться, то затраты составят 580 единиц. Найти все решения, которые могут принять предприятия как рациональные субъекты.
Решение.
Возможны следующие коалиции:
|
|
|
|
Обозначим
![]() – суммарные затраты на проводку
теплоцентралей коалициейK.
получим, что
– суммарные затраты на проводку
теплоцентралей коалициейK.
получим, что
![]() – затраты на проведение теплоцентралейi-м
предприятием
– затраты на проведение теплоцентралейi-м
предприятием
![]() ,
если оно действует в одиночку.
,
если оно действует в одиночку.
Рассмотрим условия,
при которых первому и второму предприятию
выгодно объединиться в коалицию
![]() .
Общие затраты
.
Общие затраты![]() =250
будут поделены между первым и вторым
предприятиями (необязательно поровну).
Обозначим
=250
будут поделены между первым и вторым
предприятиями (необязательно поровну).
Обозначим![]() – затраты первого предприятия,
– затраты первого предприятия,![]() – затраты второго предприятия. Очевидно,
что
– затраты второго предприятия. Очевидно,
что
![]() (3.1)
(3.1)
Каждое предприятие
сопоставляет свои затраты![]() с теми затратами, которые оно понесло,
если бы не вступило в коалицию. Для обоих
предприятий условием вступления каждого
из них в коалицию будет выполнение
следующих неравенств:
с теми затратами, которые оно понесло,
если бы не вступило в коалицию. Для обоих
предприятий условием вступления каждого
из них в коалицию будет выполнение
следующих неравенств:
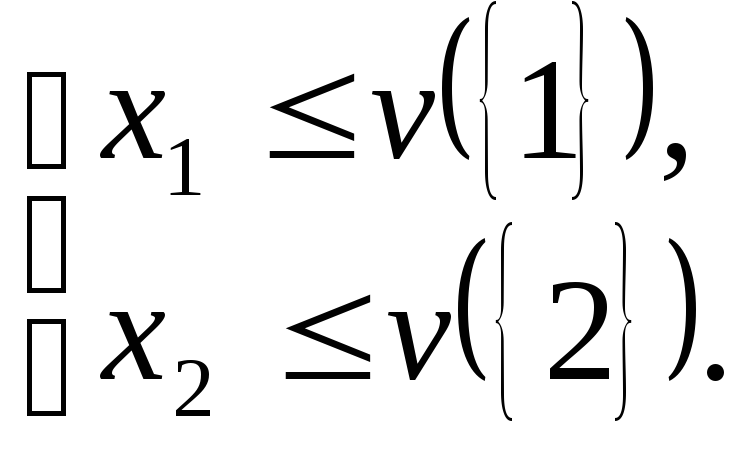 (3.2)
(3.2)
Необходимым условием для этого служит неравенство:
![]() (3.3)
(3.3)
Неравенство выполняется, т.к. 250<100+200.
Так же справедливы
неравенства 350<100+300, 460<200+300, поэтому
могут возникнуть все коалиции ![]() ,
,![]() и
и![]() .
.
При каких условиях возможна коалиция, состоящая из всех трех предприятий?
Пусть
![]() – затраты каждого из предприятия в
коалиции
– затраты каждого из предприятия в
коалиции![]() т.е.
т.е.
![]() (3.4)
(3.4)
Условием, при
котором коалиции ![]() будет выгодно
принять к себе 3-е предприятие, и при
этом вхождение в коалицию будет выгодно
3-му предприятию, будет система неравенств
будет выгодно
принять к себе 3-е предприятие, и при
этом вхождение в коалицию будет выгодно
3-му предприятию, будет система неравенств
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
Из системы следует,
что
![]() +
300≥v(
+
300≥v(![]() ).
Это неравенство не выполняется, т.к.
250+300<580. Аналогично можно сравнить
коалицию
).
Это неравенство не выполняется, т.к.
250+300<580. Аналогично можно сравнить
коалицию ![]() с двумя другими
попарными коалициями.Следовательно,
коалиция
с двумя другими
попарными коалициями.Следовательно,
коалиция ![]() менее выгодна
участникам, чем любые попарные коалиции.
менее выгодна
участникам, чем любые попарные коалиции.
Ответ. Оптимальными решениями будут коалиции, объединяющие различные пары предприятий.