Файл: Теория игр для экономистов doc.doc

K={1-е и 2-е и 3-е }UΩ, характеристическая функция коалиции {1-е и 2-е и 3-е} равна 111.

По отношению к коалиционной игре большое значение имеют следующие вопросы:

1) При каких условиях данный игрок вступает в ту или иную коалицию?

2) Как следует производить делёж общего выигрыша между членами одной коалиции?

3) Насколько устойчивы различные коалиции, и что влияет на их устойчивость?

4) Каким условиям должен соответствовать механизм принятия решений в отдельной коалиции?

В рассмотренном выше примере легко найти ответы на первые два вопроса. 1-е королевство, действуя в одиночку против двух других, получает гарантированное математическое ожидание дохода, равное 45, 2-е – 35, 3-е – 30. Если королевства являются рациональными игроками, то они будут вступать в коалиции только в тех случаях, когда их доли в дележе будут не меньше значений 45, 35 и 30 соответственно. Коалиции из двух игроков не могут обеспечить такие значения: v{1-е и 2-е}=70<45+35 и т.д. Единственным разумным коалиционным решением будет объединение всех трех в одну коалицию. Дележ 111 единиц между членами коалиции должен обеспечивать участникам доли, не меньшие тех, которые они получили бы, действуя в одиночку, т.е. v{1-е и 2-е и 3-е}=111=45+35+30+1, оставшаяся 1 может служить предметом торга.

Для общего случая коалиционной игры ответы на эти вопросы не так очевидны и требуют введения дополнительных понятий.

§3.2. Определение решения игры

Исход можно считать оптимальным только в том случае, если он может быть реализуем в условиях, когда каждая коалиция выбирает стратегии, направленные на наиболее предпочитаемые ею исходы игры. Будем обозначать S={s} множество всех исходов коалиционной игры, X_K={x_K} множество стратегий коалиции K, S(x_K) подмножество исходов, которые могут реализоваться при использовании коалицией K стратегии x_K.

Введем следующие определения.

Определение 1. Пару (K, x_K), где X_K={x_K} непустое множество, будем называть угрозой против исхода s, если все исходы из подмножества S(x_K) более предпочтительны для коалиции K, чем исход s. Будем в этом случае говорить, что коалиция K имеет угрозу x_K против исхода s.

Определение 2. Пару (Q, x_Q), где X_Q={x_Q} непустое множество, будем называть контругрозой против угрозы (K, x_K), если Q∩K непустое множество и существует по крайней мере один исход s’ из подмножества S(x_K), который менее предпочтителен, чем все исходы из подмножества S(x_Q). Будем в этом случае говорить, что коалиция Q имеет контругрозу x_Q на угрозу x_K коалиции K.

Определение 3. Угроза называется эффективной, если на нее нет контругрозы.

Определение 4. Оптимальными называются те исходы игры, против которых нет эффективных угроз. Множество всех оптимальным решением будем называть V-решением коалиционной игры, или просто решением игры.

Выясним содержательный смысл введенных определений. Пусть s некоторый исход. Если есть коалиция K, которая с помощью стратегии x_K может добиться исходов S(x_K), более благоприятных для нее, чем s, то она заинтересована в в том, чтобы исключить исход s из числа возможных и может это сделать с помощью стратегии x_K. Поэтому x_K является угрозой против исхода s. Но, с другой стороны, само существование коалиции K тоже может находиться под угрозой. Если существует коалиция Q, имеющая общих игроков с коалицией K, и применение коалицией Q некоторой стратегии x_Q приводит к исходам, более благоприятным для Q, чем один из исходов, к которым приводит стратегия x_K, то часть игроков из K может предпочесть участие в коалиции Q. Тогда образование коалиции Q может помешать образованию коалиции K, а значит помешать реализации угрозы x_K против исхода s. Угроза x_K в этом случае не является эффективной, и реализации исхода s ничто не мешает.

Таким образом, исход будет оптимальным, или потенциально реализуемым, если ни одна коалиция не заинтересована в том, чтобы исключить его из числа возможных, или каждая коалиция, которая заинтересована в этом, не может этого сделать. Применение V-решения дает возможность не рассматривать как оптимальные те исходы, против которых есть эффективные угрозы, т.е. сужает множество потенциально реализуемых исходов, что упрощает решение задачи на практике.

Пример. Парламент, состоящий из депутатов I={a,b,c,d,e,f,g} выбирает решения из множества S ={1,2,3,4,5,6,7}. Депутат a предпочитает все исходы 1,2,3 исходу 4, и все исходы 4,5,6 исходу 1. Депутат a может войти в коалицию K={a,b,c}, которая также предпочитает исходы 1,2,3 исходу 4, и может применить стратегию x_K, в результате которой может реализоваться один из исходов 1,2,3. Но a может войти в коалицию Q={a, d,e,f,g}, которая предпочитает исходу 1 любой исход из множества исходов {5,6,7}, к которым приводит стратегия x_Q. Другие коалиции кроме K и Q не могут организоваться в силу личных пристрастий депутатов. Является ли исход 4 оптимальным?

Решение.

Депутат a может предпочесть войти в коалицию Q, т.к. у нее есть стратегия x_Q, исключающая неблагоприятный для a исход 1. Следовательно, коалиция K может распасться, и стратегия x_K, угрожающая решению 4 может не осуществиться. Следовательно, исход 4 нельзя исключить из числа потенциально реализуемых, т.е. оптимальных исходов.

§3.3. Эффективность обмена. Ящик Эджворта

Рассмотрим экономику, в которой имеется два участника, которые могут обмениваться двумя благами. Суммарное количество первого блага обозначим a, суммарное количество второго блага – b. Пусть первоначально первый участник имел набор благ , а второй –. Могут ли при этом участники улучшить своё нынешнее положение, обмениваясь между собой благами, т.е. вступать в коалиции? Будем считать, что заданы функции полезности:– для первого участника и– для второго. Будем также считать, что издержки на получение информации, заключение контрактов и поиск партнёров (трансакционные издержки) равны нулю.

Для ответа на этот вопрос Эджворт предложил свою модель – Ящик Эджворта.

Рисунок 1

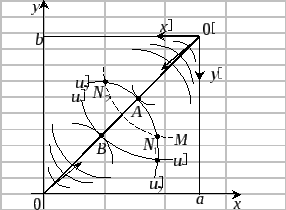
Изобразим карту кривых безразличия для каждого из участников (см. рис. 1). Можно ли улучшить положение первого участника, не ухудшая при этом положение второго.

В пределе мы получим точку A на кривой безразличия , в которой эта кривая касается кривой безразличия первого участника. Рассуждая аналогично, можно улучшить положение второго участника, не ухудшая при этом положение первого. Лучшее решение будет находиться в точкеB, где кривая касается кривой. Таким образом, мы получим множество точек, в которых кривая безразличия первого участника касается кривой безразличия второго участника. Это множество точек лежит на кривой, которая называетсяконтрактной кривой.

Рассмотрим контрактную кривую с точки зрения эффективности по Парето. На рис. 1., при переходе от точки M к точке A, первый участник улучшает своё положение, а положение второго остаётся неизменным; при переходе от точки M к точке B, положение второго участника улучшается, а положение первого остаётся неизменным. Таким образом, получается, что положение A предпочтительнее положения B, а положение B, в свою очередь, предпочтительнее положения M.

При переходе от A к B полезность одного из участников увеличивается, а полезность другого уменьшается. Такие решения называются Парето-несопоставимыми.

Множество решений, которые являются Парето-предпочтительными по сравнению с решениями, не входящими в данное множество, называют множеством Парето-эффективных решений. Таким образом, контрактная кривая является множеством решений, эффективных по Парето.

Пример. Вернёмся к вопросу об улучшении условий каждого участника при обмене.

Рисунок 2

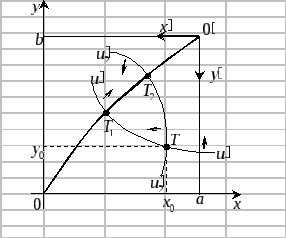
Очевидно, что первый участник согласится на обмен, при котором его кривая безразличия сдвинется вверх и вправо (Рис.2), а второй участник, согласится на обмен, при котором его кривая безразличия сдвинется вниз и влево. Таким образом, множество эффективных обменов будет лежать на контрактной кривой между точками и. Этот участок объединяет множество решений, которые могут принимать участники в ходе переговоров (торга). Именно поэтому, это множество называетсяпереговорным.

Найдём условие, которым удовлетворяют элементы переговорного множества. Условие Парето-эффективности означает, что игроки решают одну из двух задач. Либо первый игрок максимизирует свою полезность, при условии, что полезность второго игрока сохраняет своё стационарное значение, т.е.(задача 1), либо второй игрок максимизирует свою полезностьпри условии, что.

Какая именно из двух задач будет решаться, зависит от того, кто из игроков обладает большей властью или, другими словами, имеет преимущество в переговорной силе. Если такое преимущество имеет первый игрок, то будет решаться задача 1, если таким преимуществом обладает второй игрок, то решаться будет соответственно задача 2. Очевидно, что