Файл: Теория игр для экономистов doc.doc

Мы видим, что у Алисы 1-я стратегия доминирует 2-ю, т.к. 0>-1, 1>0. Поэтому Алиса выберет 1-ю стратегию. Базилио, как рациональный игрок, поймет это из анализа платежной матрицы, и тоже выберет 1-ю стратегию, т.к. в первой строке 1<0. В результате оба расскажут о ключике Карабасу.

§2.1.3. Решение игры в чистых стратегиях

Пусть дана матрица игры (игра в нормальной записи):

где A и B – участники игры. Участник A выбирает стратегию. а участникB выбирает стратегию Стратегии выбираются участниками независимо друг от друга. Выбору соответствует исходс платежом. Он равен сумме выигрыша, который получает участникаA и сумме проигрыша, который платит частник B. Естественным образом возникает вопрос: как найти лучшую стратегию для игрока A и для игрока B?

Понятие наилучшего (оптимального) решения является сложным понятием. Для того, чтобы утверждать, что какое-то решение является оптимальным, нужно знать, что именно мы понимаем под словом «оптимальный». Например, фирма, при выборе своих управленческих решений, может руководствоваться следующими соображениями:

• максимизация прибыли;

• минимизация издержек;

• завоевать место на рынке;

• стремиться к минимизации хозяйственных рисков;

• и др.

Каждое из этих соображений приводит к определенному критерию оптимальности. Решения, которые оптимальны с точки зрения одного критерия, могут быть неоптимальными с точки зрения другого. Например, если фирма выбрала в качестве критерия оптимальности принцип достижения наибольшей прибыли, то может оказаться, что решение, которое обеспечивает наибольшую прибыль, приводит к появлению высоких хозяйственных рисков.

Одним из критериев оптимальности является критерий гарантированного результата. Этот критерий заключается в том, что наилучшим решением (оптимальной стратегией) будет такое решение, которое даёт игроку определённый (гарантированный) выигрыш (или проигрыш) независимо от действий других участников игры.

В соответствии с критерием гарантированного результата игрок A для каждой своей стратегии находит наихудший для себя, а значит наилучший для соперника исход, т.е. игрок. Следовательно– столбец самых плохих результатов. Далее игрокA выбирает такое значение i, которое соответствует . Иными словами, игрок A решает задачу или задачумаксимина.

Игрок B для каждой стратегии находит наихудший результат, т.е. находитСледовательно получает строкуДалее игрокB решает задачу нахождения минимума . Другими словами, игрокB решает задачу нахождения или задачуминимакса.

Значение называетсянижним значением игры (нижняя цена игры); значение называетсяверхним значением игры (верхняя цена игры).

Теорема 1. Для любой матричной игры выполняется неравенство

(1.2)

То есть нижняя цена игры не больше чем верхняя цена игры.

Доказательство.

Зафиксируем значение i=1,2…,m и найдем наименьший элемент строки {a_i1, a_i2, …, a_in}, который обозначим a_il(i). Таким образом

_l(i) (1.3)

Обозначим a_kl(k) наибольшее из чисел {a_1l(1), a_2l(2),…, a_ml(m)}, тогда

a_kl(k)= (1.4)

Зафиксируем значение j=1,2…,n и найдем наибольший элемент столбца {a_1j, a_2j, …, a_mj}, который обозначим a_p(j)j. Таким образом

a_p(j)j =(1.5)

Обозначим a_p(q)q наименьшее из чисел { a_p(1)1, a_p(2)2,…, a_p(n)n }, тогда

a_p(q)q =(1.6)

Из (1.3) следует неравенство a_il(i)≤a_ij, верное для всех i=1.2….,m и j=1.2…,n. Подставляя в него i=k, получим неравенство

α=a_kl(k)≤a_kj (1.7)

Из (1.5) следует неравенство a_p(j)j≥a_ij, верное для всех i=1.2….,m и j=1.2…,n. Подставляя в него i=k, получим неравенство a_p(j)j≥a_kj. Итак получаем

α=a_kl(k)≤a_kj≤ a_p(j)j≤ a_p(q)q=β, что и требовалось доказать.

Если первый игрок стремится получить гарантированный результат, то он выбирает из своего множества стратегий стратегию k, для которой наименьшее значение выигрыша равно нижнему значению игры α. Тогда при любом выборе вторым игроком стратегии j будет верно неравенство a_ij≥ α, то есть α является гарантированным выигрышем первого игрока.

Аналогично, если второй игрок стремится получит гарантированный результат, то он выберет стратегию q, для которой наибольшее значение проигрыша будет равно верхнему значению игры β. Тогда при любом выборе первым игроком стратегии i будет верно неравенство a_ij≤β, то есть β является гарантированным верхним значением проигрыша второго игрока.

Будет ли исход игры, реализующийся при стратегиях k и q, равновесным зависит от того, равны или нет числа α и β.

Если верхняя цена равна нижней цены игры, т.е. выполняется равенство:

(1.8)

то число называетсячистой ценой игры.

Пусть платёжная матрица удовлетворяет уравнению (1.8). Это значит, что существует её элемент a_lk, для которого верно равенство

(1.9)

Исход достигается, когда игрокA выбирает стратегию l, а игрок B – стратегию k. В этом случае стратегия k называется оптимальной минимаксной стратегией игрока B, а элемент называетсяседловой точкой (седлом) платёжной матрицы. Совокупность (цена игры оптимальной стратегии) называетсярешением игры в чистых стратегиях.

Теорема 2. Если один участник игры выбирает свою оптимальную (максиминную/минимаксную) стратегию, то лучшим выбором для другого участника будет своя (минимаксная/максиминная) стратегия.

Доказательство. Пусть игрок A выбрал свою оптимальную стратегию , тогда для любых стратегийигрокаB будет справедливо неравенство . Для оптимальной стратегииигрокаB будет выполняться неравенство , следовательно для, а для. Из этого следует, что наилучшей стратегией для игрокаB будет стратегия . Аналогично доказывается обратная зависимость.

Итак, если платёжная матрица имеет седловую точку, то ни одному участнику игры не выгодно в одностороннем порядке отказываться от своей оптимальной (максиминной/минимаксной) стратегии. Другими словами в cедловой точке наблюдается баланс интересов, поэтому эту точку называют точкой равновесия.

Если платёжная матрица имеет седловую точку, то:

1. Игрок A имеет оптимальную максиминную стратегию;

2. Игрок B имеет минимаксную стратегию;

3. Применение оптимальных стратегий даёт ситуацию равновесия, которая оказывается равновесием в чистых стратегиях.

4. Игра имеет решени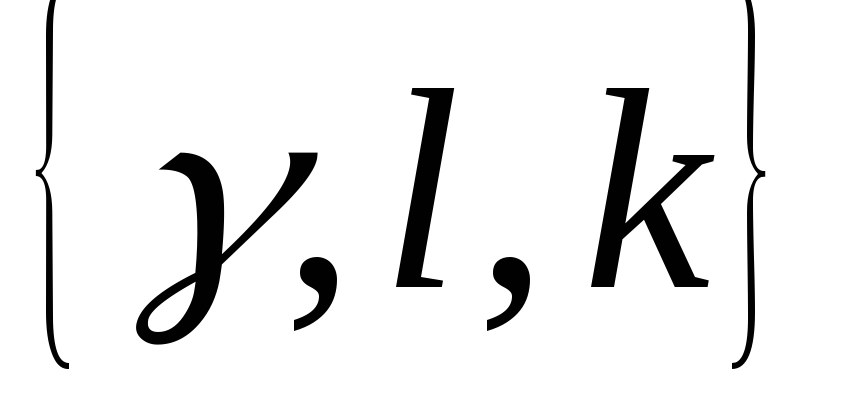е , где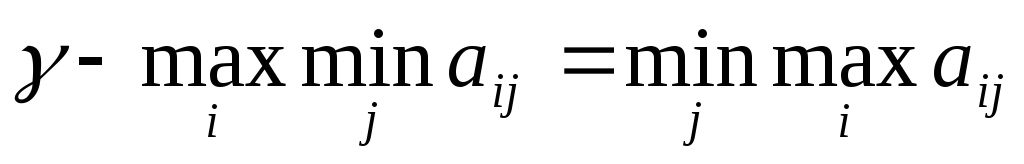.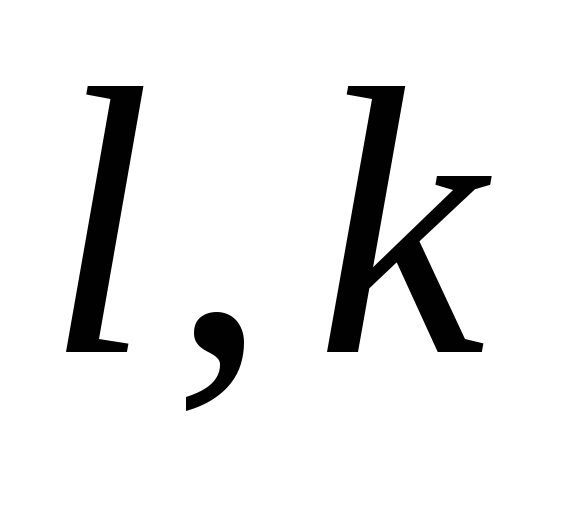- оптимальные стратегии..

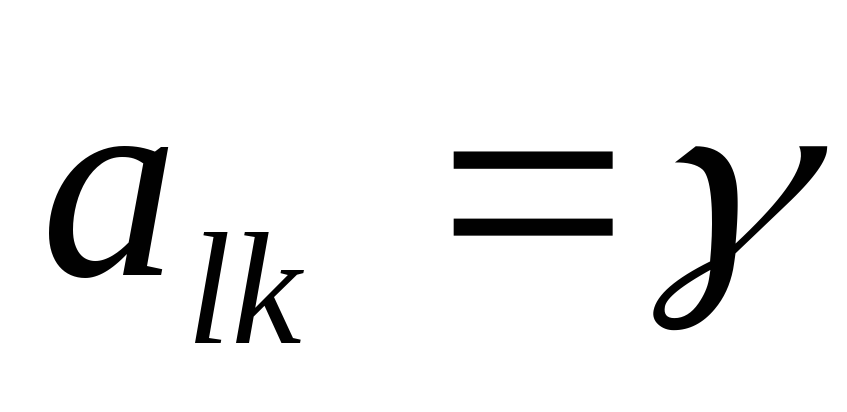Пример. Найти решение игры.

Решение.Игрок A руководствуясь принципом гарантированного результата. Для этого он в каждой строке ищет минимальный элемент, затем максимальное значение в полученном столбце минимумов