ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 374
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
![]()
![]() –выигрыш n-го
участника.
–выигрыш n-го
участника.
Всё множество выигрышей можно описать следующим образом:
![]() –множество
выигрышей (проигрышей), т.е. результат
игры 1-го участника;
–множество
выигрышей (проигрышей), т.е. результат
игры 1-го участника;
![]() –результат игры
дл 2-го участника;
–результат игры
дл 2-го участника;
![]()
![]() –результат игры
n-го
участника.
–результат игры
n-го
участника.
Итак, для формального описания игры необходимо:
задать множество игроков –
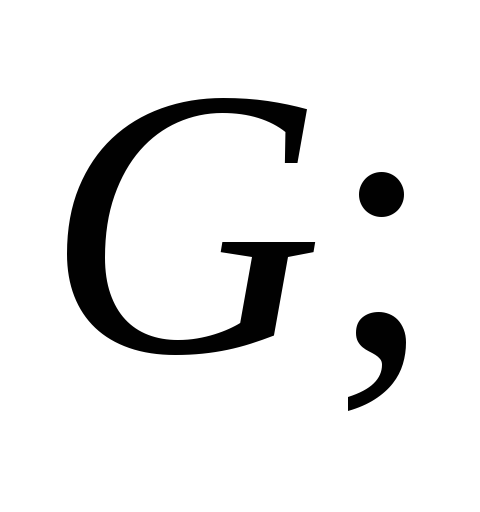
задать для каждого из них множество стратегий –
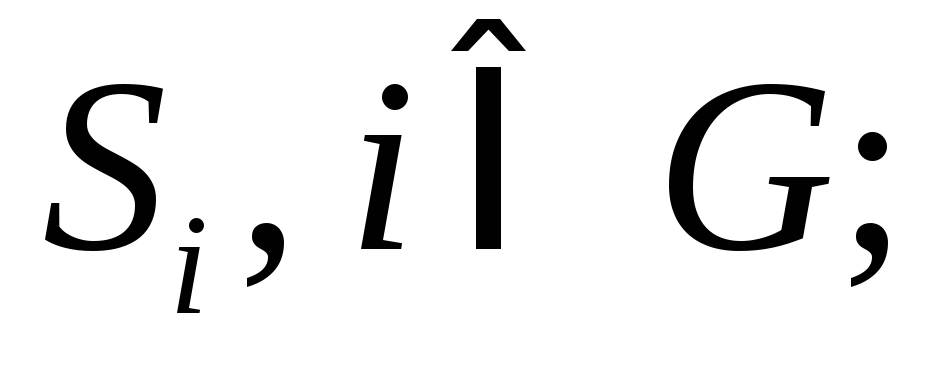
задание функций выигрышей (проигрышей) игроков для каждого из возможных исходов игры (платёжная функция).
§1.3. Классификация игр
Игры можно разделить на классы по множеству различных признаков. Например, по количеству игроков: игры с 2-мя участниками, игры с 3-мя участниками, и т.д. Очевидно, что игра с двумя участниками является самой простой моделью. Принципиальные различия между играми производятся по следующим признакам:
1) Могут ли участники игры объединяться в группы для выработки совместных решений. Если участники игры могут объединяться в группы, принимающие совместные решения, то игра называется коалиционной или кооперативной. В противном случае – бескоалиционной или некооперативной. Нетрудно понять, что в коалиционной игре набор возможных решений каждого участника намного шире, чем в бескоалиционной игре. Следовательно, более сложной является модель конфликта между участниками.
2) На основании какой информации принимают решения участники игры. Наиболее простым является случай, когда все участники, во-первых, знают все множество возможных исходов игры, т.е. ситуаций, к которым приводят все допустимые комбинации стратегий игроков, и, во-вторых, знают количественные значения индивидуальных полезностей всех игроков для каждого исхода. Формальное описание такой игры с полной информацией приведено в §1.2., в данном пособии рассматриваются только такие игры. Но в реальных конфликтах участники не всегда располагают такой информацией, или одни участники являются более информированными, чем другие. Такие конфликты моделируются играми с неполной информацией, более сложными в смысле нахождения решения, чем игры с полной информацией.
3) Однократно или многократно производится розыгрыш игры. Если одна и та же игровая ситуация воспроизводится множество раз (многократное разыгрывание), то игра называется повторяющейся. Такие игры описаны в §2.2.5. данного пособия.
4) Действуют ли участники игры одновременно, или действия одних участников следуют за действиями других. В последнем случае игра называется последовательной. Такие игры описаны в §2.2.6. данного пособия.
5) Отдельный класс игр представляют собой динамические (или дифференциальные) игры. Эти игры являются моделями конфликтных задач управления динамическими объектами, движение которых описывается дифференциальными уравнениями. В данном пособии такие игры не рассматриваются.
Имеются также другие признаки выделения игр в отдельные классы, например, различия игровых возможностей игроков, или их переговорных сил, игры, в которых отдельные игроки могут изменять правила игры и т.д. Эти игры, представляющие большой практический интерес, не входят в данное пособие, ознакомиться с ними можно в монографии Гермейер Ю.Б. Игры с непротивоположными интересами.
В данном пособии игры классифицируются на коалиционные и бескоалиционные, последние с свою очередь разделяются на игры с противоположными интересами (антагонистические) и игры с непротивоположными интересами (неантагонистические).
Глава 2. Бескоалиционные игры
§2.1. Антагонистические игры
§2.1.1. Понятие антагонистической игры. Матричная игра.
Антагонистическими называются игры, в которых результат, выгодный одному участнику всегда невыгоден другому. Другое название таких игр – игры с противоположными интересами. Частным случаем игры с противоположными интересами является игра с постоянной суммой.
Рассмотрим игру с постоянной суммой, в которой участвуют два игрока. Будем считать, что каждый игрок имеет конечное множество стратегий. Будем также считать, что при любом исходе игры, сумма выигрышей двух участников равна постоянному числу H. Тогда формальное описание игры будет следующим:
Множество участников
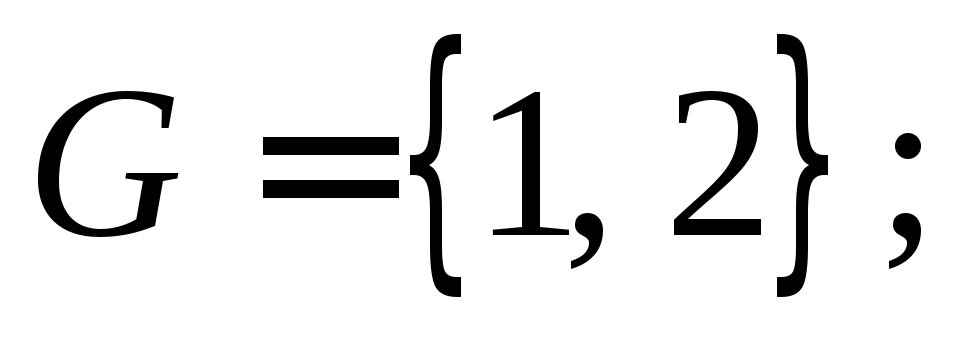
Множество стратегий
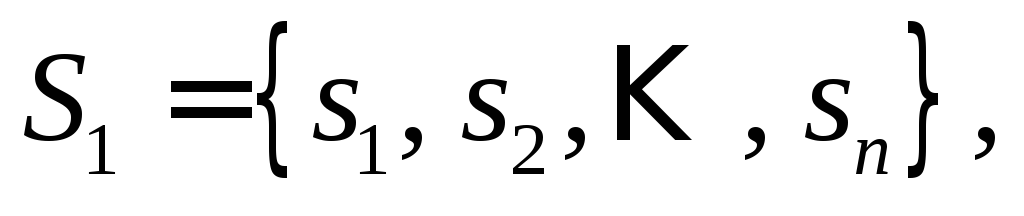
![]()
Множество исходов
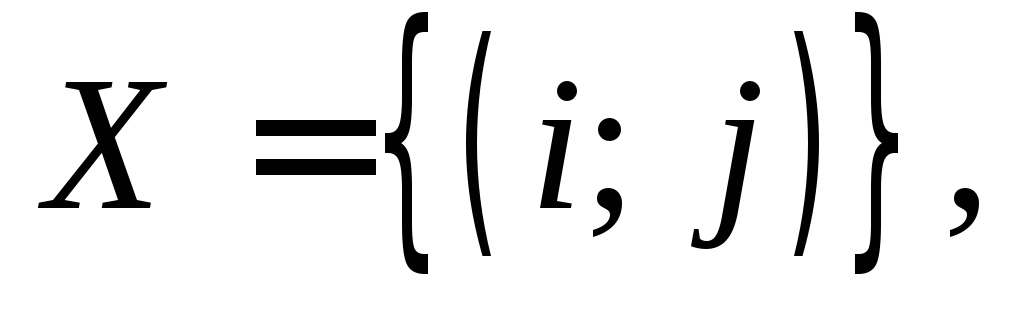 i
– номер стратегии 1-го участника; j
– номер стратегии 2-го участника.
i
– номер стратегии 1-го участника; j
– номер стратегии 2-го участника.Платёжная функция.
![]() –выигрыш 1-го
участника для исхода
–выигрыш 1-го
участника для исхода
![]() ;
;
![]() –выигрыш 2-го
участника для исхода
–выигрыш 2-го
участника для исхода
![]()
![]() Предположим, что
при некотором исходе выигрыш некоторого
(1-го участника) равен:
Предположим, что
при некотором исходе выигрыш некоторого
(1-го участника) равен:
![]()
![]() .
.
То есть, при каждом
исходе 1-й участник получает
![]() а 2-й – теряет
а 2-й – теряет![]() Таким образом, игру с постоянной суммой
можно представить какигру
с нулевой суммой:
при каждом исходе, выигрыш 1-го участника
равен проигрышу 2-го участника.
Таким образом, игру с постоянной суммой
можно представить какигру
с нулевой суммой:
при каждом исходе, выигрыш 1-го участника
равен проигрышу 2-го участника.
Игру с нулевой суммой можно представить в виде таблицы, в клетках которой указываются значения выигрыша 1-го участника (равные проигрышу 2-го участника). Таким образом, игру с нулевой суммой можно задать с помощью матрицы:
(1.1)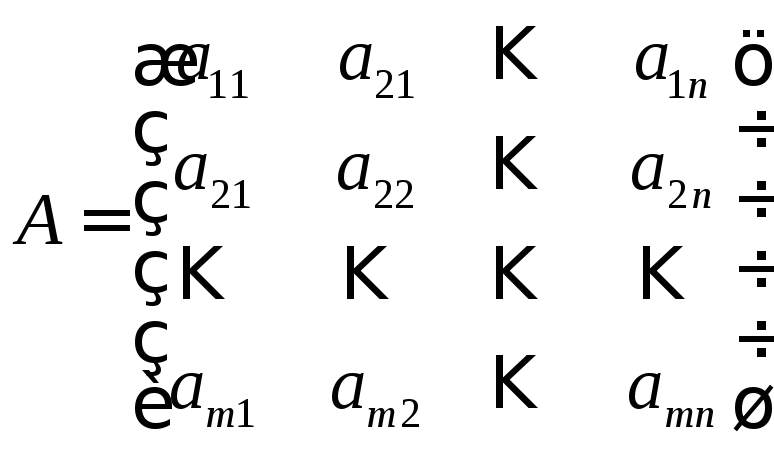
Номер строки соответствует номеру стратегии 2-го участника, номер столбца соответствует номеру стратегии 1-го участника.Матрица A в называется платёжной матрицей. Представление игры с помощью платежной матрицы называют нормальной записью игры (или нормальным представлением игры).
Очевидно, что 1-й игрок предпочитает те исходы, в которых значение элемента платежной матрицы будет наибольшим, а 2-й игрок исходы, в которых соответствующий элемент будет наименьшим. Однако, исход зависит от выбора обоими игроками своих стратегий. Поэтому, рациональный игрок при выборе своей стратегии должен просчитывать, какие стратегии предпочтет его соперник. Решением игры будем называть исход игры, рассчитанный в предположении, что игроки рациональны, т.е. оптимизируют свой результат на основе какого-либо разумного критерия.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
В этом параграфе пойдет речь о попарном сравнении между собой стратегий игрока. Иногда в результате такого сравнения делается вывод о превосходстве (т.е. доминировании) одной стратегии над другой. Рассмотрим пример.
Пример. Дана платёжная матрица A:
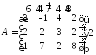
Первый игрок выбирает строку,
второй выбирает столбец.
В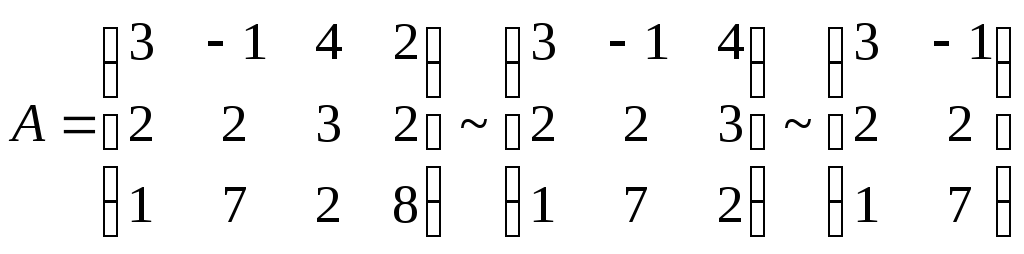

 торой
игрок может заметить, что элементы 4-го
столбца
торой
игрок может заметить, что элементы 4-го
столбца![]() соответствующих элементов 2-го столбца.
А как было указано выше второй участник
стремиться минимизироватьаij
Значит, при любых действиях соперника
2-я стратегия оказывается лучше или не
хуже, чем 4-я. В таких случаях говорят,
что 2-я стратегия доминирует над 4-й.
Следовательно, 4-ю стратегию 2-й участник
может вычеркнуть, аналогично. продолжая
рассуждения исравнивая
1 и 3 стратегии второго игрока, платёжная
матрица примет следующий вид: случаях
говорят, что 2-я стратегия доминирует
над 4-й. Следовательно, 4-ю стратегию 2-й
участник может вычеркнуть, аналогично.
продолжая рассуждения исравнивая
1 и 3 стратегии второго игрока, платёжная
матрица примет следующий вид:
соответствующих элементов 2-го столбца.
А как было указано выше второй участник
стремиться минимизироватьаij
Значит, при любых действиях соперника
2-я стратегия оказывается лучше или не
хуже, чем 4-я. В таких случаях говорят,
что 2-я стратегия доминирует над 4-й.
Следовательно, 4-ю стратегию 2-й участник
может вычеркнуть, аналогично. продолжая
рассуждения исравнивая
1 и 3 стратегии второго игрока, платёжная
матрица примет следующий вид: случаях
говорят, что 2-я стратегия доминирует
над 4-й. Следовательно, 4-ю стратегию 2-й
участник может вычеркнуть, аналогично.
продолжая рассуждения исравнивая
1 и 3 стратегии второго игрока, платёжная
матрица примет следующий вид:
В последней матрице нет таких двух строк, чтобы элементы одной строки были больше соответствующих элементов другой строки, а также таких столбцов, чтобы элементы одного столбца были меньше соответствующих элементов другого столбца, следовательно, дальнейших преобразований не будет.
Дадим общее определение доминирования стратегий.
Говорят, что стратегия l доминирует стратегию k для 1-го участника, если для всех значений j=1,2…,n справедливы неравенства alj≥akj, и хотя бы для одного значения j неравенство является строгим.
Аналогично:
Говорят, что стратегия l доминирует стратегию k для 2-го участника, если для всех значений i=1,2…,m справедливы неравенства ail≤aik, и хотя бы для одного значения i неравенство является строгим.
Вычёркивание доминируемых стратегий называется редукцией (сокращением игры). В результате редукции уменьшается размерность платёжной матрицы.
В некоторых играх может существовать стратегия одного из игроков, которая доминирует все остальные его стратегии. Действуя рационально, данный игрок будет использовать только эту стратегию, которая называется доминирующей. Очевидно, что доминирующая стратегия, если она существует, дает наибольший выигрыш, следовательно, является оптимальной. Другой игрок, зная домиинрующую стратегию своего соперника, также определяет свою оптимальную стратегию: это стратегия, дающая ему наибольший выигрыш при условии, что соперник использует доминирующую стратегию. Таким образом, данная игра имеет равновесие, т.е. исход, от которого нет оснований отклоняться каждому из игроков. Полученное решение игры называется решением в доминирующих стратегиях.
Пример.Кот Базилио и лиса Алиса узнали, где спрятан золотой ключик. Каждый из них может сказать об этом либо Карабасу, либо черепахе Тортилле. Если оба расскажут черепахе, или оба расскажут Карабасу, то оба получат одинаковую награду (для простоты возьмем ее за 0). Если один расскажет черепахе, а другой Карабасу, то Карабас заберет один золотой у того, кто рассказал черепахе, и отдаст золотой тому, кто рассказал Карабасу. Найти рациональные стратегии Алисы и Базилио.
Решение. Составим платежную матрицу:
|
Базилио |
|
||||||
|
|
Карабасу |
Черепахе |
|
||||
|
Алиса |
Карабасу |
0 |
1 |
||||
|
Черепахе |
-1 |
0 |
|||||