ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 357
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
Решение игры в смешанных стратегиях.
Задания для практических занятий.
№24.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№25.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№26.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№27.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№28.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№29.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№30.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
Ответ:
![]() - смешанные стратегии игрока 1;
- смешанные стратегии игрока 1;![]() - смешанные стратегии игрока 2;
- смешанные стратегии игрока 2;![]() - цена игры.
- цена игры.
№31. Игра состоит в следующем. Имеются две карты: туз и двойка. Игрок А наугад вынимает одну из них; В не видит, какую карту он вынул. Если А вынул туза, он заявляет: «у меня туз», и требует у противника 1 рубль. Если А вынул двойку, то он может либо А1) сказать «у меня туз» и потребовать у противника 1 рубль, либо А2) признаться, что у него двойка, и уплатить противнику 1 рубль. Противник, если ему добровольно платят 1 рубль, может только принять его. Если же у него потребуют рубль, то он может либо В1) поверить игроку А, что у него туз, и отдать ему 1 рубль, либо В2) потребовать проверки с тем, чтобы убедиться, верно ли утверждение А. Если в результате проверки окажется, что у А действительно туз, В должен уплатить А 2 рубля. Если же окажется, что А обманывает и у него двойка, игрок А уплачивает игроку В 2 рубля. Требуется проанализировать игру и найти оптимальную стратегию каждого из игроков.
Ответ:
|
А В |
В1 (верить) |
В2 (не верить) |
|
А1 (обманывать) |
1 |
0 |
|
А2 (не обманывать) |
0 |
0,5 |
Решения игры в
чистых стратегиях нет.
![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В;
- смешанные стратегии игрока В;![]() - цена игры.
- цена игры.
№32. Сторона А посылает в район расположения противника В два бомбардировщика I и II; I летит спереди, II – сзади. Один из бомбардировщиков – заранее неизвестно какой – должен нести бомбу, другой выполняет функцию сопровождения. В районе противника бомбардировщики подвергаются нападению истребителя стороны В. Бомбардировщики вооружены пушками различной скорострельности. Если истребитель атакует задний бомбардировщик II, то по нему ведут огонь пушки только этого бомбардировщика; если же он атакует передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков. Вероятность поражения истребителя в первом случае 0,3, во втором 0,7. Если истребитель не сбит оборонительным огнем бомбардировщиков, то он поражает выбранную им цель с вероятностью 0,6. Задача бомбардировщика – донести бомбу до цели; задача истребителя – воспрепятствовать этому, т.е. сбить бомбардировщик-носитель. Требуется выбрать оптимальные стратегии сторон: для стороны А - какой бомбардировщик сделать носителем; для стороны В - какой бомбардировщик атаковать?
Ответ:
|
А В |
В1 (атаковать бомбард. I) |
В2 (атаковать бомбард. II) |
|
А1 (носитель – бомбард. I) |
0,82 |
1 |
|
А2 (носитель – бомбард. II) |
1 |
0,58 |
Решения игры в
чистых стратегиях нет.
![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В;
- смешанные стратегии игрока В;![]() - цена игры.
- цена игры.
№33. Спортивный клуб А располагает тремя вариантами состава команды А1, А2, А3. Клуб В – также тремя вариантами В1, В2, В3. Подавая заявку для участия в соревновании, ни один из клубов не знает, какой состав изберет противник. Вероятности выигрыша клуба А при различных вариантах составов команд, примерно известные из опыта прошлых встреч, заданы матрицей:
|
А В |
B1 |
B2 |
B3 |
|
A1 |
0,8 |
0,2 |
0,4 |
|
A2 |
0,4 |
0,5 |
0,6 |
|
A3 |
0,1 |
0,7 |
0,3 |
Найти, с какой частотой клубы должны выставлять каждый из составов во встречах друг с другом, чтобы добиться наибольшего в среднем числа побед.
Ответ:
![]() - смешанные стратегии клуба А;
- смешанные стратегии клуба А;![]() - смешанные стратегии клуба В;
- смешанные стратегии клуба В;![]() - цена игры.
- цена игры.
№34.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
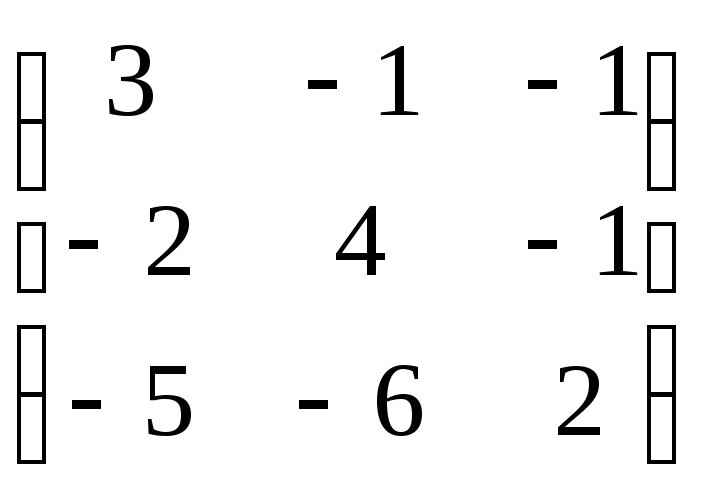 .
.
Ответ:
![]() - смешанные стратегии игрока А;
- смешанные стратегии игрока А;![]() - смешанные стратегии игрока В;
- смешанные стратегии игрока В;![]() - цена игры.
- цена игры.
Задания для самостоятельного решения.
№35.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
№36.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
№37.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
№38.
Решить графически игру, заданную
платежной матрицей:
![]() .
.
№39.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
 .
.
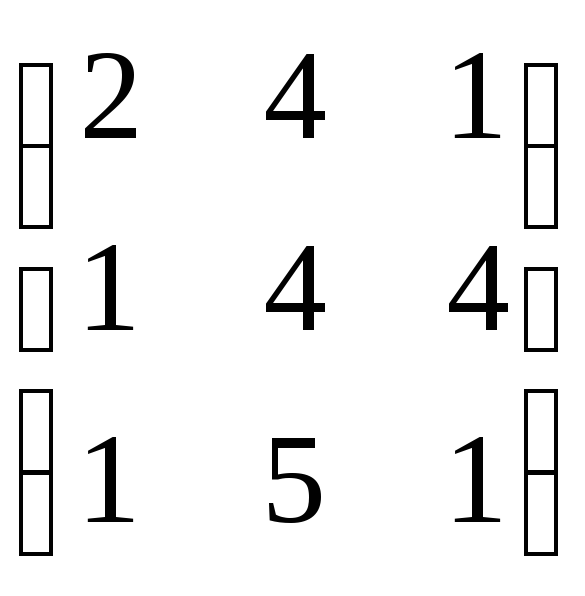
№40.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
 .
.
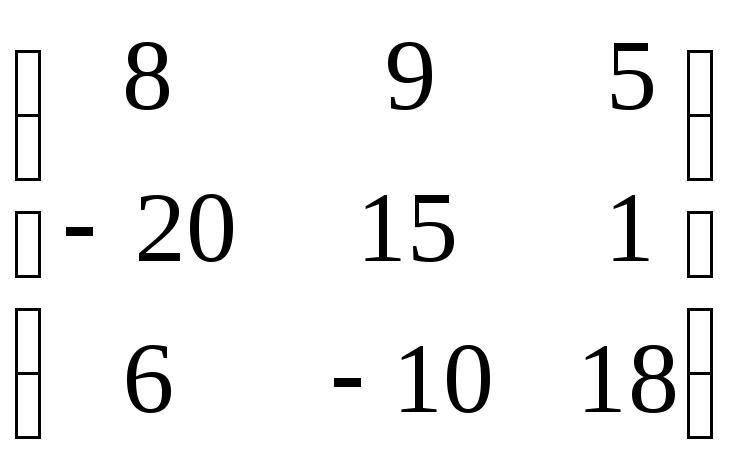
№41.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
 .
.
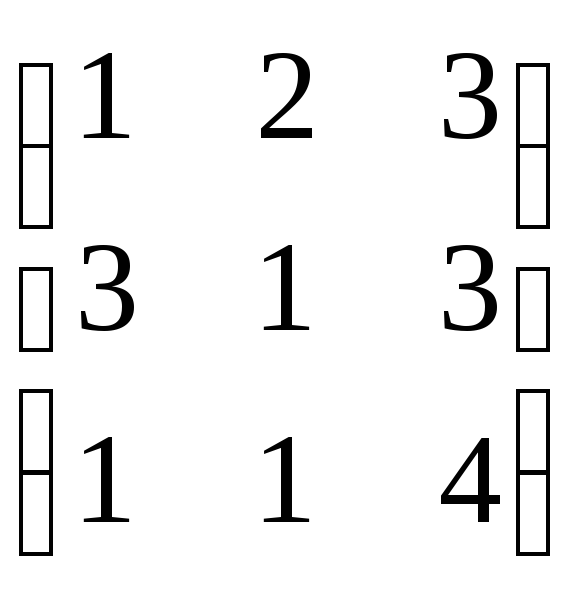
№42.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
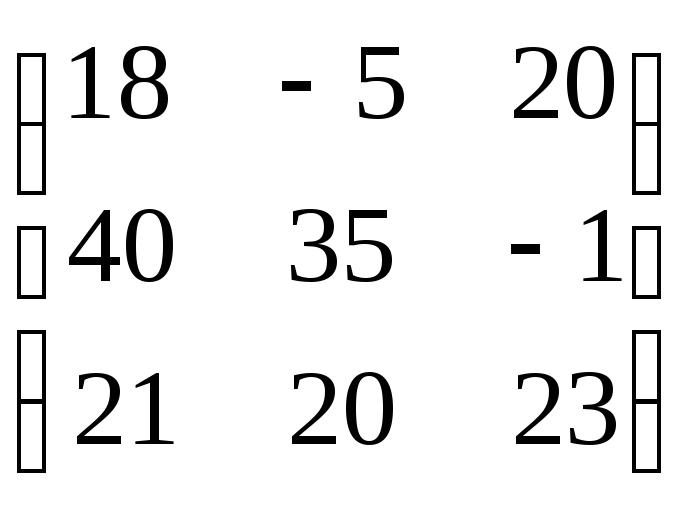 .
.
№43.
Найти решение в смешанных стратегиях,
предварительно убедившись, что решения
в чистых стратегиях нет, для игры,
заданной платежной матрицей:
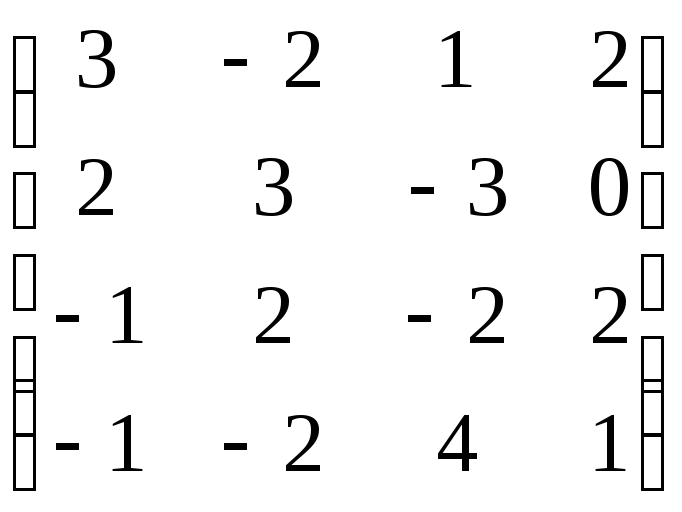 .
.