Файл: Теория игр для экономистов doc.doc

Решим задачу 1, т.е.

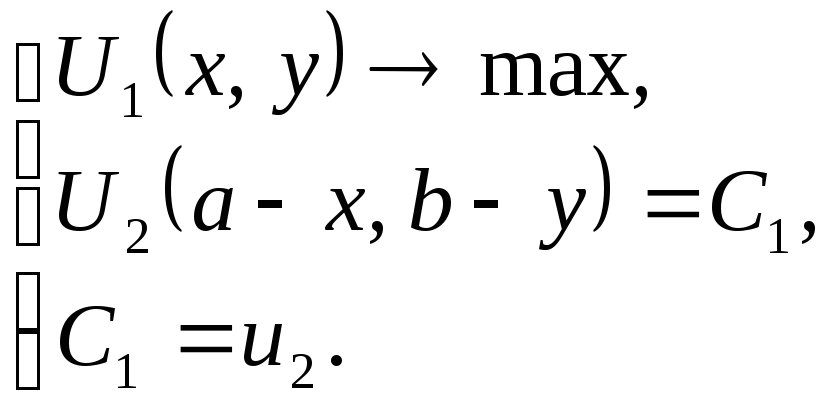
Имеем задачу нахождения условного экстремума для функции . Для её решения используем функцию Лагранжа.

Найдём частные производные и приравняем их к нулю.

.

Отсюда получаем условие первого порядка (необходимое условие экстремума, касающиеся первых производных)

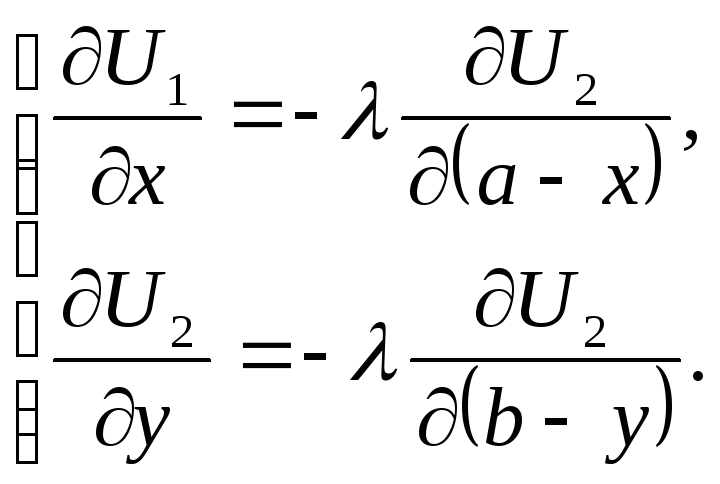
Исключая параметрполучим уравнение:

(3.7)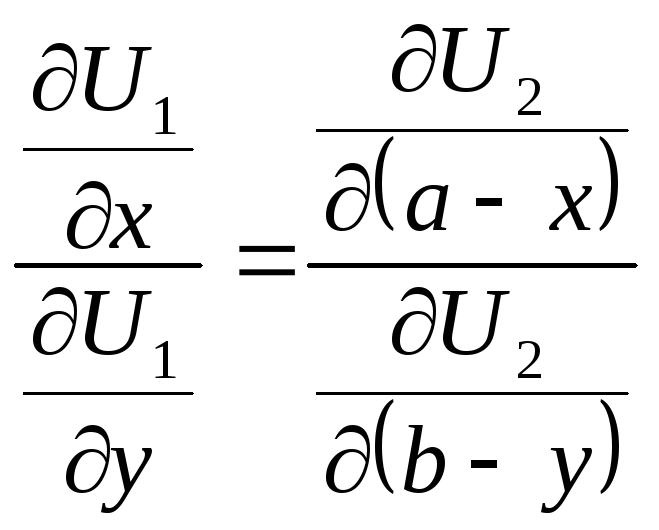

В уравнении (3.7) предельные полезности продуктов обмена для первого игрока

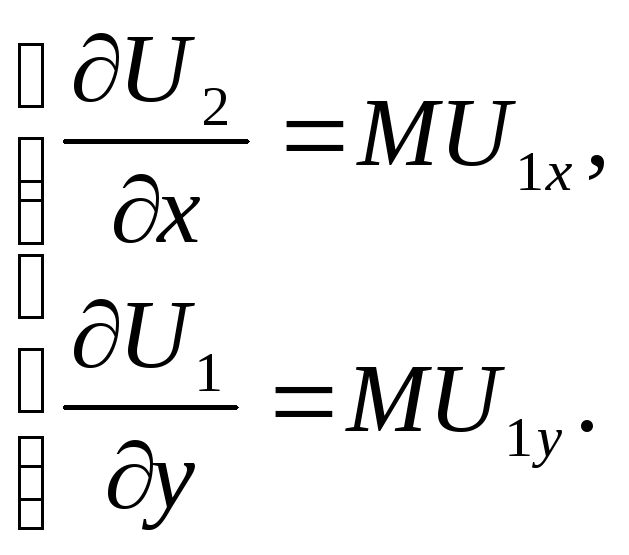
Предельная норма замещения продукта x продуктом y для первого игрока будет в этом случае равна:

.

Т

(3.8)

Следовательно, все точки на контрактной кривой удовлетворяют уравнению (3.8). К уравнению (3.8) нужно добавить условия индивидуальной рациональности:

(3.9)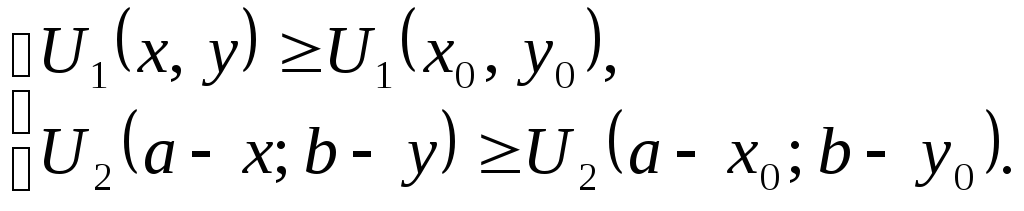

Решение задачи максимизации полезности вторым игроком (задача 2) будет аналогичным.

Если оба продукта x и y являются нормальными товарами, то можно показать, что в некоторой точке переговорного множества будет выполняться и условие второго порядка. Следовательно, контрактная кривая описывается уравнением (3.8). Переговорное множество удовлетворяет уравнению (3.8) и системе неравенств (3.9).

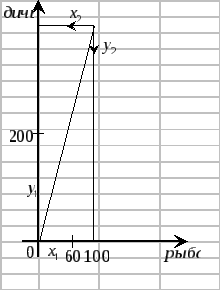
Пример. Два туземных племени живут охотой и рыболовством. Для того, чтобы природные ресурсы не истощались, правительство установило общие квоты на отлов рыбы и отстрел дичи: рыбы – не более 100 тонн в год; дичи – не более 400 тонн в год.

Первоначально первое племя добывало 60 тонн рыбы и 20 тонн дичи, а второе племя добывало 40 тонн рыбы и 20 тонн дичи.

Предположим, что каждое из племён имеет собственную функцию полезности:

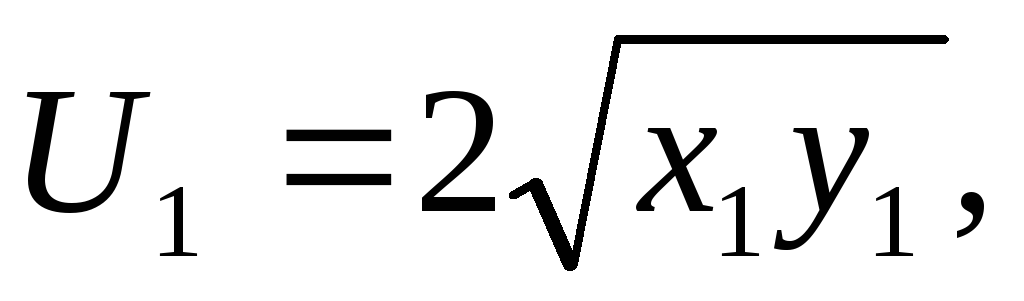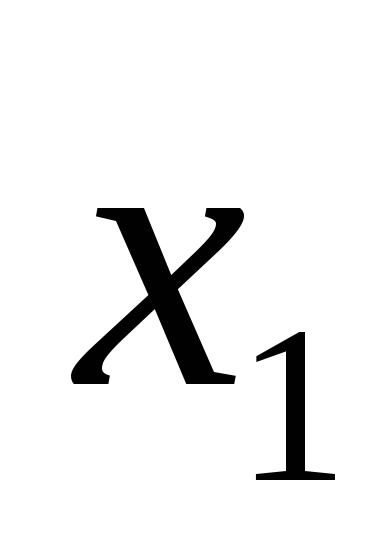• где – количество рыбы, а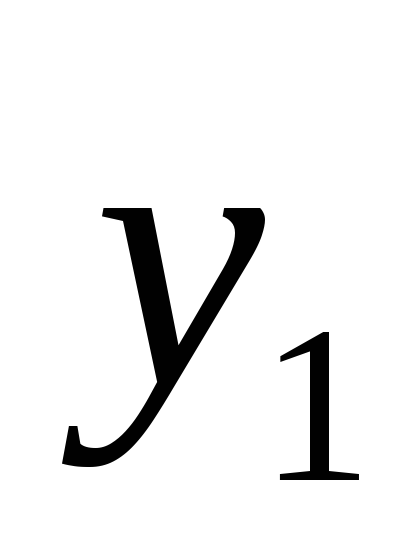– количество дичи;

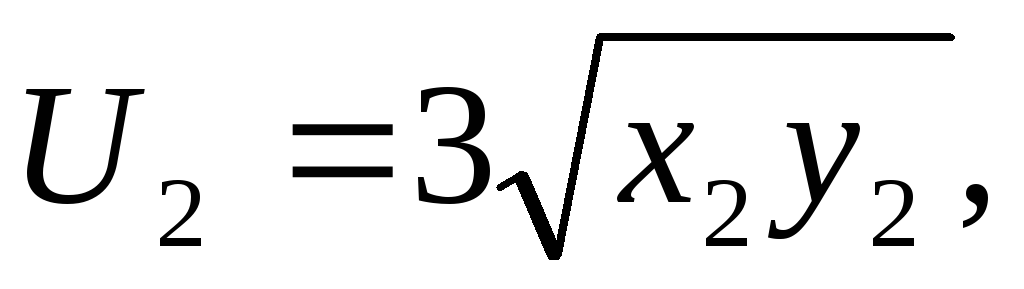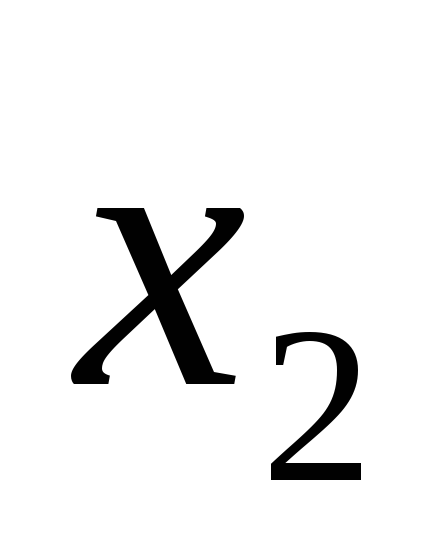• где – количество рыбы, а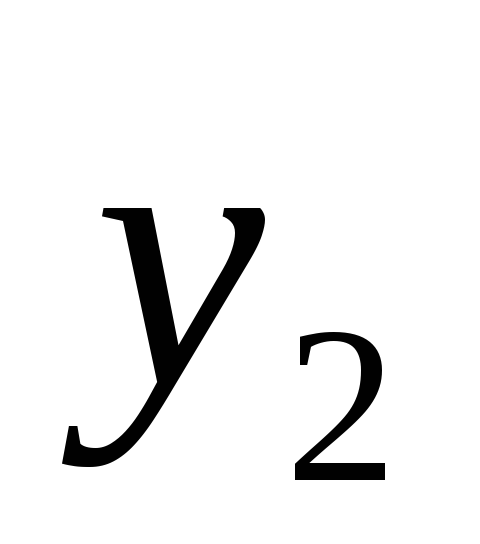– количество дичи.

Вожди обоих племён собрались и решили заключить соглашение об охоте и рыболовстве, выполнение которого должно увеличить полезность каждого племени. Требуется найти множество контрактов, улучшающих положение каждого племени, т.е. необходимо найти контрактную кривую.

Решение. Изобразим ящик Эджворта (см. рис.3.)

Рисунок 3

(_*)

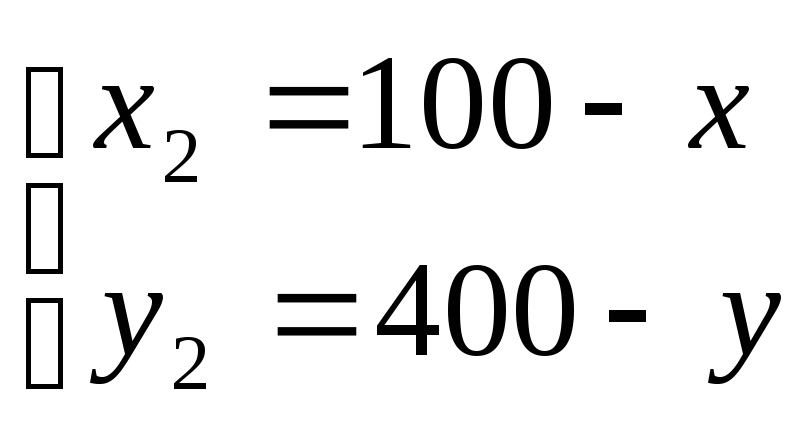
Найдём уравнение контрактной кривой, для чего обратимся к функции (3.8). Найдём предельные нормы замещения:

П

(_**)

(***)

Уравнение (_***) – уравнение контрактной кривой.

Для того, чтобы на контрактной кривой определить переговорное множество, нужно найти полезности каждого племени в точке угрозы:

Найдём полезность каждого племени в точках на контрактной кривой:

.

Получаем условия индивидуальной рациональности.

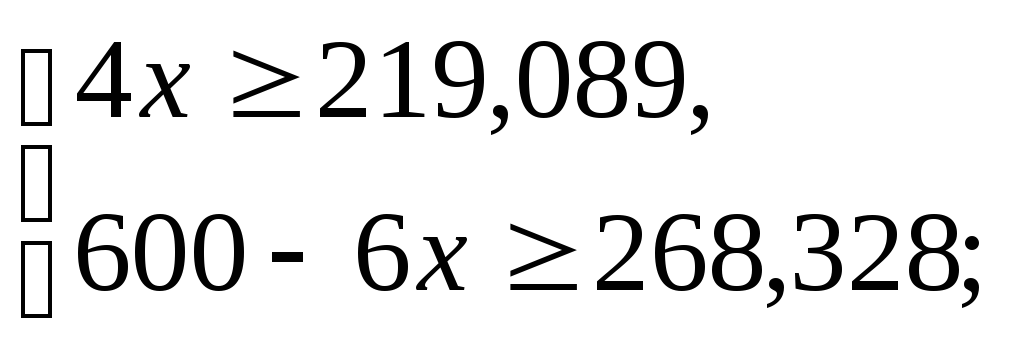
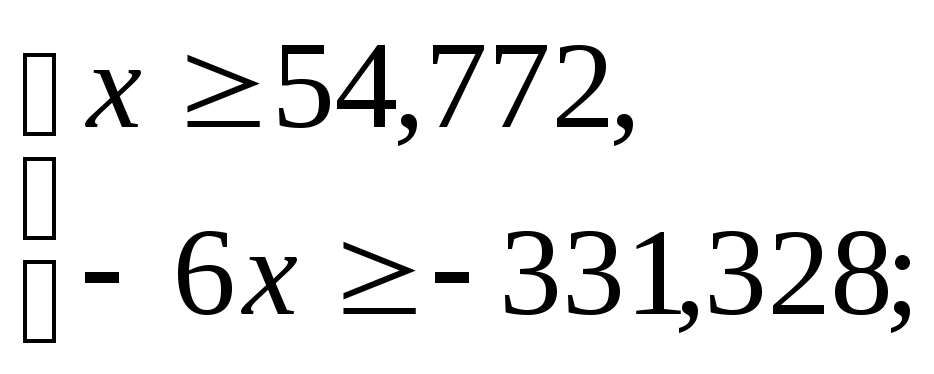
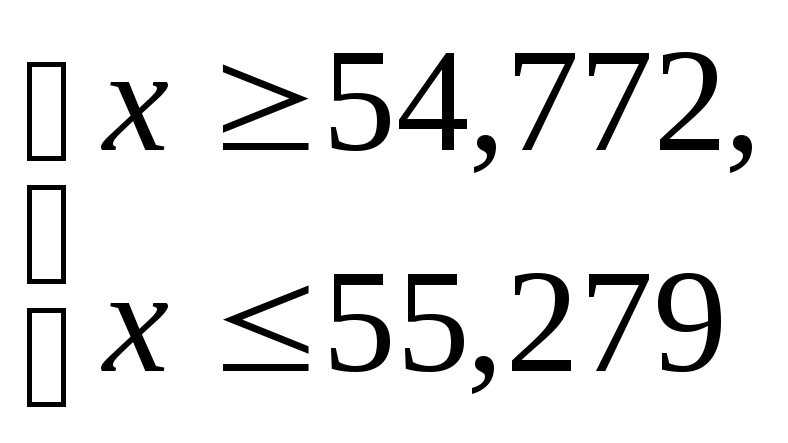
§3.4. Арбитражное решение

Рассмотрим ящик Эджворта и построим в нём переговорное множество (см. рис. 4).

Рисунок 4

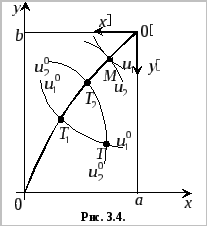
Построим контрактную кривую . ТочкаT, находящаяся на пересечении двух кривых и, является точкой угрозы. Отрезок на кривой контрактов между точкамиипредставляет собой переговорное множество.

Каждой точке на кривой контрактов соответствует определённые значения полезностей каждого из участникови. Таким образом, каждой точке на кривой контрактов соответствует пара чиселиВсей кривой контрактов соответствует геометрическое множество точек на координатной плоскости(см. рис. 5.).

Рисунок 5

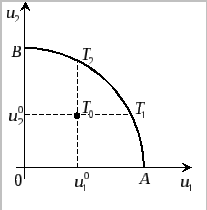
На рис.5. в точке 0 аНа рис. 3.5. этой точке соответствует точка с координатами. В точкена рис. 3.4.аНа рис.5 ей соответствует точка с координатами.

Двигаясь из точки в точку, мы будем увеличивать полезность первого игрока и уменьшать полезность второго. Получим кривуюAB. Она называется кривой Парето-эффективных решений для данной игры (иногда эту кривую называют множеством Парето-оптимальных решений). Изобразим на рис. 5. точку T₀ , гдеи– полезности участников в точке угрозы. Условием заключения контракта будут условия индивидуальной рациональности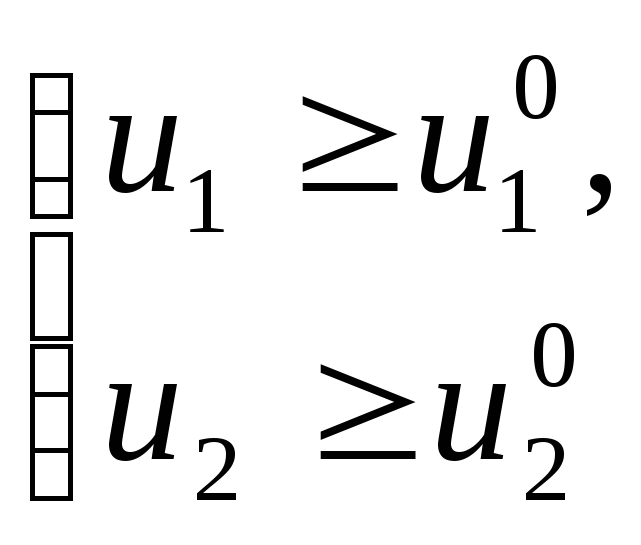. На рис.5 этим условиям будет соответствовать дуга.

Дуга представляет собой переговорное множество, которое, в свою очередь, являетсяподмножеством множества Парето-эффективных решений, для которого выполняются условия индивидуальной рациональности.

Любая точка на кривой для каждого из участников лучше, чем точкаT₀. Переход из любой точки кривой в другую точку этой кривой улучшает положение одного из участников, ухудшая при этом положение другого. Возникает вопрос о существовании какого-либо оптимального компромиссного решение?

Д. Нэш доказал, что существует (при том единственное) решение задачи с торгом, удовлетворяющее следующим критериям:

1. Решение является эффективным (оптимальным) по Парето.

2. Полезность каждого участника при этом решении не меньше, чем в точке угрозы.

3. Решение не изменится, если сумма общего выигрыша будет преобразована по линейному закону 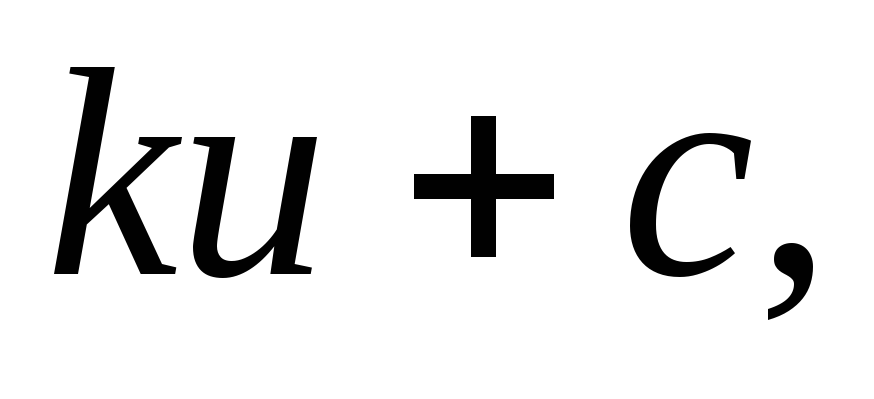где– первоначальная сумма общего выигрыша;и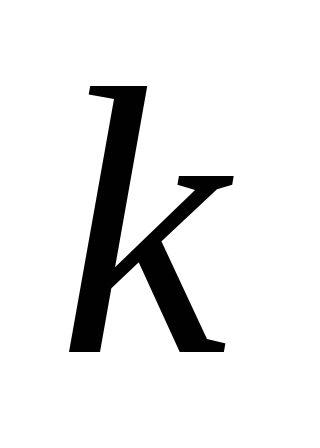–Это свойство называетсяинвариантностью относительно линейного преобразования.

4. Решение не изменится, если перенумеровать участников игры (свойство симметрии).

5. Независимость от альтернатив, не имеющих отношения к делу. Это значит, что все возможные альтернативы, которые рациональные игроки не будут использовать, можно исключить из рассмотрения.

Нэш доказал, что решением, которое удовлетворяет всем вышеперечисленным критериям, является решение, для которого функция достигает своего максимума на множестве точек переговорного множества⁷. Решение справедливо для любого конечного числа игроков. Если имеются два игрока, то решение Нэша принимает вид:

,