ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 351
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
№3. Для отопления коттеджа в зимний период используется уголь, цена на который зависит от времени года и характера зимы. Летом тонна угля стоит 7,5 ден. ед., в мягкую зиму – 8,5, в обычную – 9,0, а в холодную – 9,5. Расход угля в отопительный сезон полностью определяется характером зимы: в мягкую зиму достаточно 6 т., в обычную требуется 7 т., а в холодную расходуется 8 т. Понятно, что затраты домовладельца зависят от количества запасенного им с лета угля. При анализе возможных вариантов уровня запаса следует иметь в виду, что при необходимости недостающее количество угля можно приобрести зимой. Кроме того, надо учесть, что продать непотребовавшийся уголь возможности не будет. Используя игровой подход, составить платежную матрицу.
Ответ:
|
Д З |
малая зима |
обычная зима |
холодная зима |
|
малая зима |
45 |
54 |
64 |
|
обычная зима |
52,5 |
52,5 |
62 |
|
холодная зима |
60 |
60 |
60 |
№4. Фирмы Ф1 и Ф2 производят сезонный товар, пользующийся спросом в течение n единиц времени. Доход от продажи товара в единицу времени составляет C ден. ед. Фирма Ф2, будучи более состоятельной, в ходе конкурентной борьбы стремится вытеснить фирму Ф1 с рынка сбыта, способствуя своими действиями минимизации ее дохода, не считаясь при этом с временными потерями части своего дохода в надежде наверстать упущенное в будущем. Действующее законодательство не позволяет злоупотреблять для этого заведомым занижением цены на товар (прибегать к демпинговым ценам). Единственным допустимым способом достижения своей цели для фирмы Ф2 (как и для фирмы Ф1 в целях защиты своих интересов на рынке сбыта) остаются повышение качества товара и надлежащий выбор момента времени поставки его на рынок сбыта. Уровень спроса на товар зависит от его качества, и в данный момент реализуется тот товар, качество которого выше. Повышение же качества требует дополнительных затрат времени на совершенствование технологии его изготовления и переналадки оборудования. В связи с этим будем предполагать, что качество товара тем выше, чем позже он поступает на рынок. Придать описанной ситуации игровую схему и построить платежную матрицу (для n = 5).
Ответ: Аi (i = 1, 2, …, 5) – чистая стратегия игрока А, состоящая в том, что он поставит свой товар в i-ую единицу времени; Bj (j = 1, 2, …, 5) – чистая стратегия игрока B, состоящая в том, что он поставит свой товар в j-ую единицу времени;
|
Ф1 Ф2 |
В1 |
В2 |
В3 |
В4 |
В5 |
|
А1 |
2,5С |
С |
2С |
3С |
4С |
|
А2 |
4С |
2С |
С |
2С |
3С |
|
А3 |
3С |
3С |
1,5С |
С |
2С |
|
А4 |
2С |
2С |
2С |
С |
С |
|
А5 |
С |
С |
С |
С |
0,5С |
№5.
Используя понятие доминирования,
уменьшить размерность платежной матрицы:
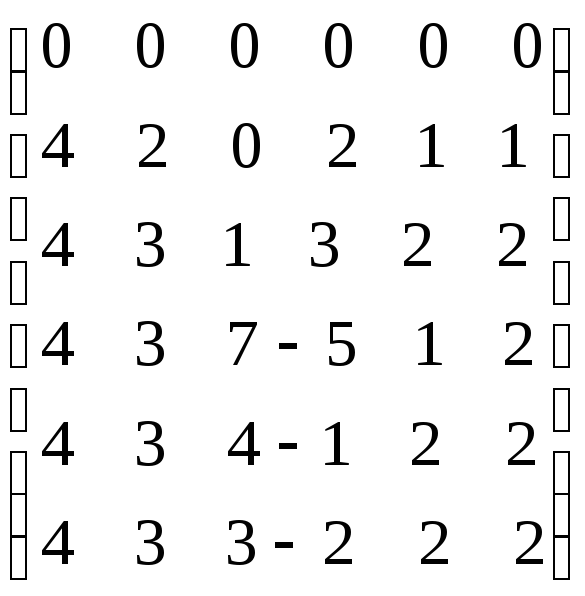 .
.
Ответ:
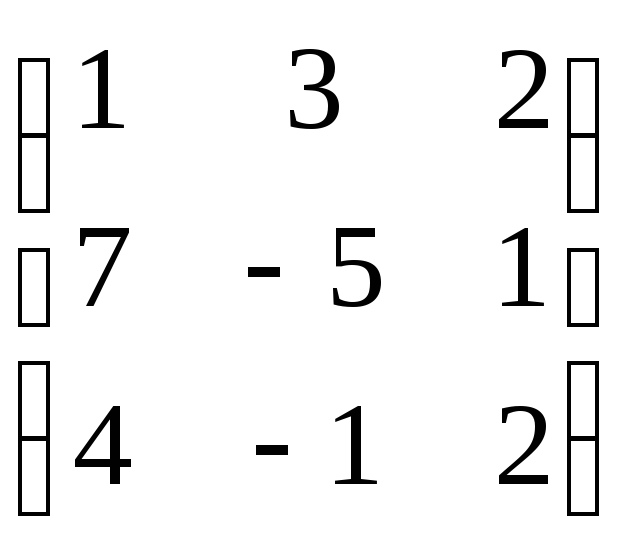 .
.
Задания для самостоятельного решения.
№6. Два игрока А и В, не глядя друг на друга, кладут на стол по монете вверх гербом или вверх цифрой, по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или у обоих цифра), то игрок А забирает обе монеты; иначе их забирает игрок В. Сформулировать ситуацию в терминах теории игр. Представить игру в нормальной и развернутой формах.
№7. Игроки А и В одновременно и независимо друг от друга записывают каждый одно из трех чисел: 1, 2 или 3. Если сумма написанных чисел четная, то В платит А эту сумму в рублях; если она нечетная, то, наоборот, А платит В эту сумму. Сформулировать ситуацию в терминах теории игр. Представить игру в нормальной и развернутой формах.
№8. Армия полковника сражается с противником за контроль над двумя позициями. Полковник имеет 2 полка, а противник – 3. И полковник, и противник посылают свою армию на сражение в полном составе. И полковник, и противник могут послать на каждую позицию целое число полков. Позиция будет захвачена армией с большим числом полков. Составить платежную матрицу игры.
№9.
Используя понятие доминирования,
уменьшить размерность платежной матрицы:
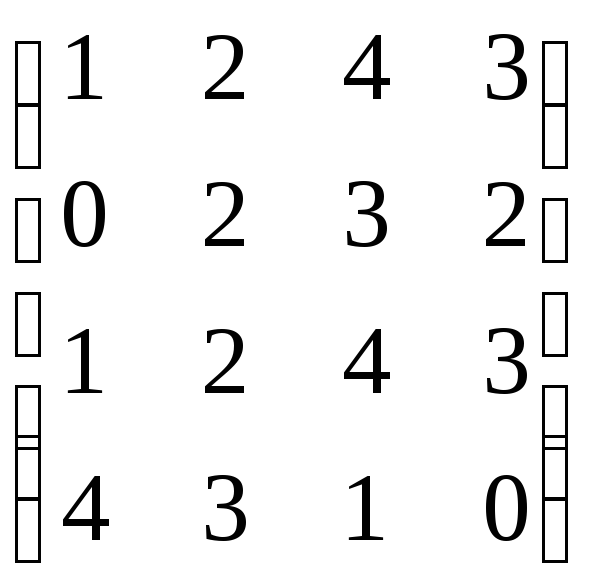 .
.
Решение игры в чистых стратегиях.
Задания для практических занятий.
№10. Предприниматели А и В продают однородный товар. А может рекламировать свой товар по радио (А1), по телевидению (А2), через газеты (А3). В может рекламировать свой товар по радио (В1), по телевидению (В2), через газеты (В3), через торговых агентов (В4). Процент привлеченных клиентов предпринимателями А и В в зависимости от выбранной каждым стратегии задан платежной матрицей:
|
А В |
В1 |
В2 |
В3 |
В4 |
|
А1 |
8 |
-2 |
9 |
-3 |
|
А2 |
6 |
5 |
6 |
8 |
|
А3 |
-2 |
4 |
-9 |
5 |
Найти решение игры в чистых стратегиях.
Ответ:
![]()
№11.
Определить максиминную и минимаксную
стратегии и решение игры в чистых
стратегиях, если оно существует, для
игры, заданной платежной матрицей:
 .
.
Ответ:
![]()
№12.
Определить максиминную и минимаксную
стратегии и решение игры в чистых
стратегиях, если оно существует, для
игры, заданной платежной матрицей:
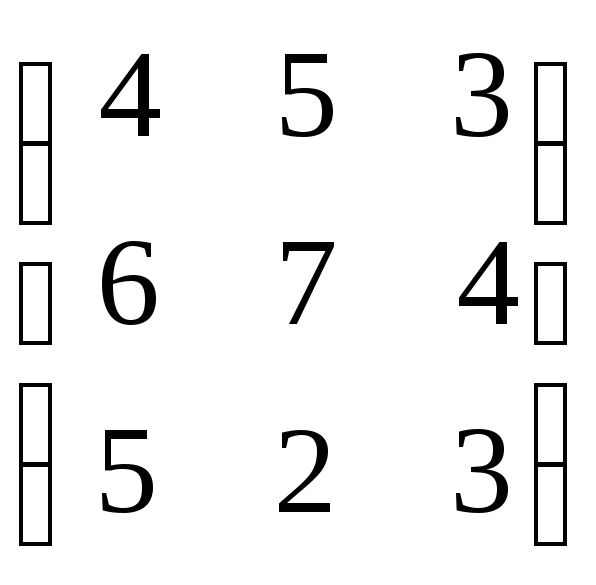 .
.
Ответ:
![]()
№13.
Определить седловую точку и цену игры,
заданной платежной матрицей:
 .
.
Ответ:
![]()
№14.
Определить седловую точку и цену игры,
заданной платежной матрицей:
 .
.
Ответ:
![]()
№15.
Указать диапазон цены игры, заданной
платежной матрицей:
 .
.
Ответ:
![]()
№16.
Дана платежная матрица. Указать область
значений параметров p
и q,
если седловая точка (2; 2):
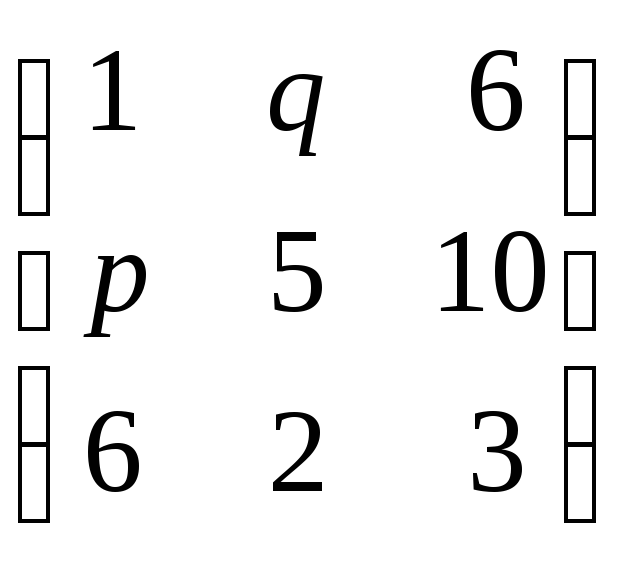 .
.
Ответ:
![]()
№17.
Найти максиминную и минимаксную
стратегии, нижнюю и верхнюю цены игры,
заданной платежной матрицей:
 .
.
Ответ:
![]()
Задания для самостоятельного решения.
№18.
Найти нижнюю и верхнюю цены игры,
предварительно упростив ее:
 .
.
№19.
Определить максиминную и минимаксную
стратегии и решение игры в чистых
стратегиях, если оно существует, для
игры, заданной платежной матрицей:
 .
.
№20.
Определить максиминную и минимаксную
стратегии и решение игры в чистых
стратегиях, если оно существует, для
игры, заданной платежной матрицей:
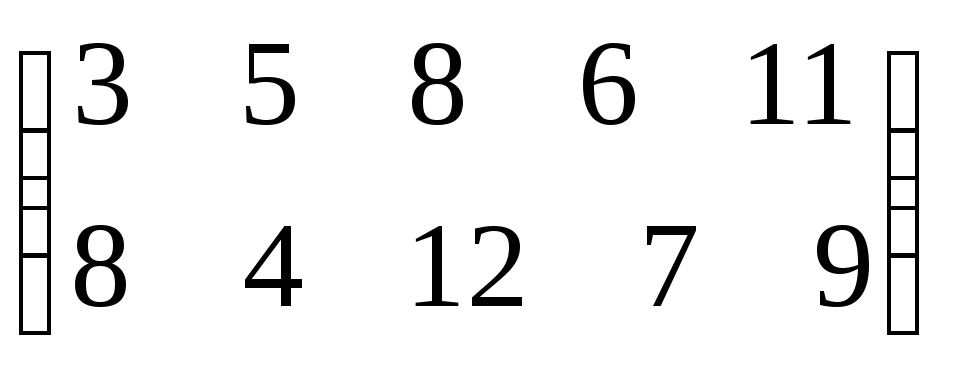 .
.
№21.
Определить максиминную и минимаксную
стратегии и решение игры в чистых
стратегиях, если оно существует, для
игры, заданной платежной матрицей:
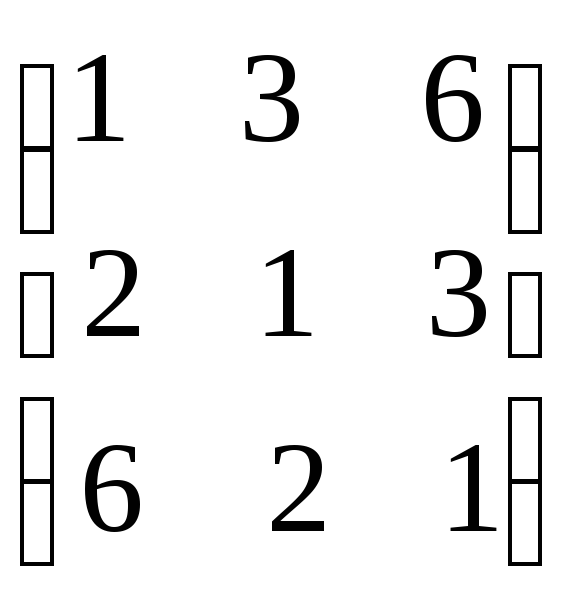 .
.
№22.
Определить седловую точку и цену игры,
заданной платежной матрицей:
 .
.
№23.
Указать диапазон цены игры, заданной
платежной матрицей:
 .
.