Файл: Теория игр для экономистов doc.doc

Пояснение. Уравнение означает, что стратегияявляется лучшим отве­том второго участника на стратегиюпервого участника, т.е.

.

Уравнение означает, что первый участник выбирает стратегию таким обра­зом, что в случае рационального выбора второго участника, первый участник получит свой наибольший выигрыш. Здесь мы предполагаем, что право первого хода принадлежит первому участнику. Аналогично можно сформулировать определение оптимальной стра­тегии по Штакельбергу в случае, если первый ход принадлежит второму участнику. В некоторых играх право первого хода даёт преимущество тому участнику, который им обладает.

Пример. «Игра на опережение».

Ситуация дуополии на рынке фирм-производителей сухих завтраков. Обе фирмы выпускают одинаковую продукцию: сырки и хлопья. Первая фирма доминирует на рынке и первой приступает к выпуску продукта. Прибыли обеих фирм приведены в таб­лице 13:

Таблица 13

Найти равновесие по Штакельбергу.

Решение. В игре существует два равновесия по Нэшу . Если бы фирмы выбирали продукты одновременно, то равновесием в игре было бы равновесие по Нэшу. Вспомним, что первая фирма обладает правом первого хода и запишем развёрнутую форму игры (рис. 2 )

Рисунок 2

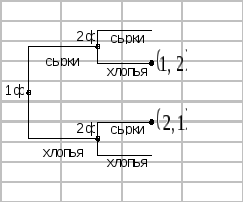
Двигаясь по дереву игры от конца к началу, мы приходим к выводу, что оптимальной стратегией по Штакельбергу для первой фирмы будет выбор сырков, а для второй - хлопьев. Таким образом, равновесие по Штакельбергу достигается в исходе.

Легко проверить, что равновесие по Нэшу всегда является равновесием по Штакельбергу (иллюстрацией служит пример «Игра на опережение»), но обратное не всегда верно.

Также преимущества первого хода проявляется в конкуренции по Курно⁶ между двумя фирмами. Дуополия по Курно представляет собой модель, в которой два конкурирующих производителя однородной продукции выбирают свой выпуск, исходя из заданной функции совокупного спроса и из предположения, что конкурент максимизирует свою прибыль, принимая выпуск другой фирмы является постоянным. Таким образом, фирмы начинают с монопольной цены, а затем последовательно снижают цены до равновесного значения. Рассмотрим пример.

Пример. «Дуополия Курно»

Рынок поделён между двумя фирмами, каждая из которых выбирает свой объём выпуска: – выпуск первой фирмы;– выпуск второй фирмы. Совокупный вы­пуск (предложение) будет равен

(2.18)

Уравнение кривой спроса на данном рынке задано и имеет вид:

(2.19)

Требуется определить равновесную цену, если право первого хода принадлежит первой выпуск.

Решение. По формуле найдём выручку первой фирмы

(2.20)

Аналогично, выручка второй фирмы будет равна:

(2.21)

По формуле вычисления прибыли находим прибыль каждой из фирм:

,

.

Предположим сначала, что каждая фирма является монополистом, следовательно, может выбирать выпуск, максимизирующий ее прибыль при постоянном выпуске конкурента. Оптимум (максимум прибыли) достигается в точке, где предельная выручка равна предельным издержкам, т.е.:

Для упрощения будем считать, что

тогда первая фирма выбирает выпуск при котором. Вторая фирма выбирает выпуск, при котором.

Предельная выручка фирм определяется как частная производная от выручки по объёму выпуска. Таким образом:

Найдём значение оптимальные значения и

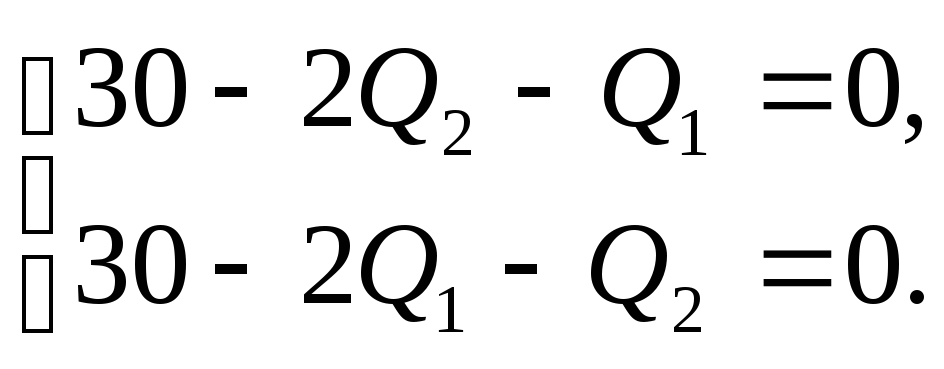(2.22)

Система (2.22) получается в предположении, что каждая фирма максимизирует свою выручку и предполагает, что её конкурент сделает то же самое.

Находим значение и выручки обеих фирм:

Если бы фирмы могли договориться между собой, то они бы выбрали такой выпуск , который максимизировал бы их общую выручку

.

При этом а выпуск каждой из фирм, при справедливом дележе, был бы равен. Однако реализации этого исхода препятствует очередность ходов, которая дает преимущества фирме, обладающей правом первого хода.

Для простоты, будем считать, что каждая фирма выбирает один из трёх объёмов выпуска: 7,5; 10 и 15. В таблице 14 приведены выручки каждой из фирм для всех всевозможных исходов:

Таблица 14

Равновесным по Нэшу является исход с результатами (). Теперь предположим, что первая фирма обладает правом первого хода, т.е. она выбирает объём выпуска и сообщает об этом второй фирме, которая, в свою очередь, выбирает объем выпуска, максимизирующий прибыль при заданном объеме выпуска конкурента. Таким образом, получаем следующие исходы:

• первая фирма –7,5;тогда вторая фирма –10,результат(93,75; 125);

• первая фирма –10;тогда вторая фирма –10,результат(100; 100);

• первая фирма –15;тогда вторая фирма –7,5,результат(112,5; 56,25).

Сравнивая полученные исходы по прибыли первой фирмы, находим равновесие по Штакельбергу, находящееся в исходе с результатами ,выпуски фирм при этом.Первая фирма выигрывает за счёт права первого хода, вторая фирма при этом теряет часть прибыли по сравнению с равновесием по Нэшу..

В реальности первая фирма, выбрав объём производства должна убедить вторую фирму в том, что она не намерена отступать от этой стратегии. Для этого она может проводить рекламную компанию, вкладывать деньги и т.д. такие действия называютсястратегическим ходом.

Стратегическим называется ход, который влияет на выбор другого игрока в благоприятном направлении для игрока, делающего стратегический ход.

Влияние заключается в том, что стратегический ход воздействует на ожидание второго игрока относительно поведения первого. Таким образом, стратегический ход ограничивает выбор партнёра, предварительно ограничив собственное поведение. Делая стратегический ход, участник игры связывает себя обещаниями, вкладывает средства в действия, которые вынуждают партнёра выбирать благоприятные для первого участника стратегии. Но может оказаться, что второй участник не поверит стратегическому ходу первого игрока и сочтёт его действия пустой угрозой.

Пример. «Пустые угрозы при наличии доминирующих стратегий»

На рынке действуют две фирмы. Первая фирма производит многофункциональные мобильные телефоны, а вторая – простые. Если вторая фирма назначит низкую цену, то часть покупателей первой фирмы перейдёт на потребление продукции второй фирмы. Если же первая назначит низкую цену, то у второй фирмы останется лишь один выход – назначить более низкую, чем у первой фирмы цену. Прибыли фирм в зависимости от выбранных стратегий приведены в таблице 15.

Таблица 15