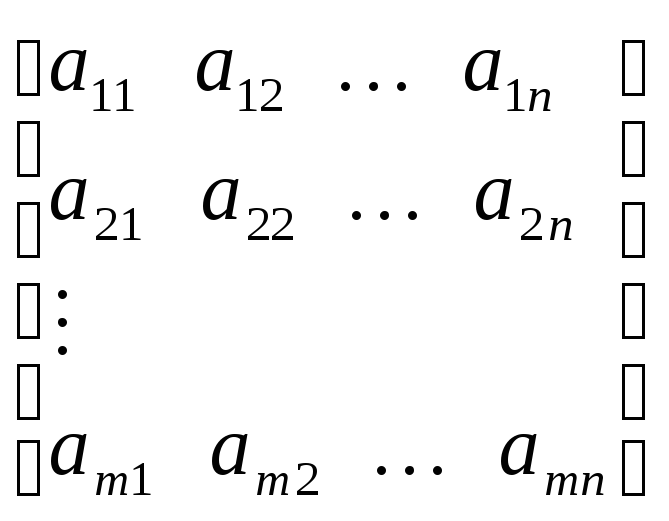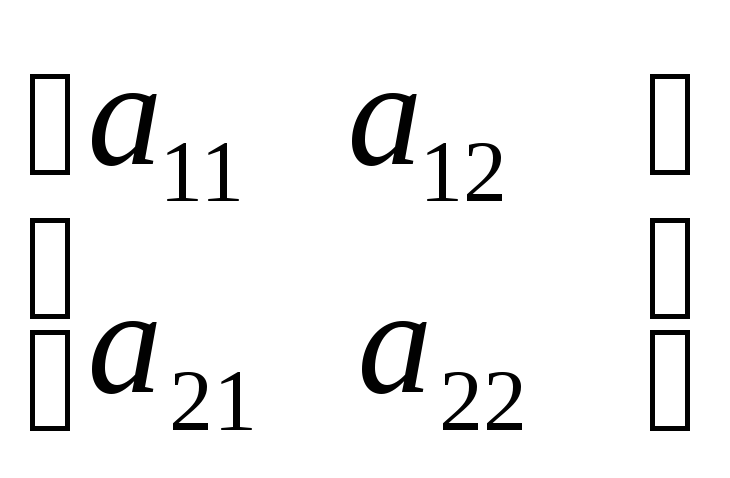ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 361
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
![]() ≥H(x,y(x)), подставляя
в последнее неравенство x=x~,
получим
≥H(x,y(x)), подставляя
в последнее неравенство x=x~,
получим
![]() ≥H(x~,y(x~))
(1.26)
≥H(x~,y(x~))
(1.26)
В неравенство (1.25) подставим y= y(x~), получим
α≤ Η(x~, y(x~) (1.27)
Из неравенств
(1.26) и (1.27) следует
![]() .,
что и требовалось доказать
.,
что и требовалось доказать
Свойство 2.
Пусть
![]() – верхнее значение игры в чистых
стратегиях, а
– верхнее значение игры в чистых
стратегиях, а![]() – верхнее значение игры в смешанных
стратегиях. Тогда
– верхнее значение игры в смешанных
стратегиях. Тогда
![]()
Доказывается аналогично свойству 1.
Свойство 3.
Нижняя чистая цена игры и верхняя чистая
цена игры ограничивают значение сверху
и снизу значение игры в смешанных
стратегиях:
![]() .
.
Доказательство следует из теоремы (4) и свойств (1) и (2).
Свойство 4.
Если матричная игра имеет равновесие
в чистых стратегиях, то чистое значение
игры
![]() равно значению игры в смешанных
стратегиях, то есть при
равно значению игры в смешанных
стратегиях, то есть при![]() будет справедливо
будет справедливо
![]()
Доказательство следует из свойства (3).
В случае, когда
матричная игра имеет седловую точку,
оптимальная смешанная стратегия первого
игрока
![]() будет иметь вид
будет иметь вид
![]() .
.
И оптимальная смешанная стратегия 2-го игрока будет иметь вид
![]() .
.
Таким образом, равновесия в чистых стратегиях является частным случаем равновесия в смешанных стратегиях.
5. Теорема об активных стратегиях.
Стратегия i
первого игрока называется его активной
стратегией,
если в оптимальной стратегии
![]() вероятность
вероятность![]() .
Аналогично стратегияj
игрока 2 называется его активной
стратегией,
если в оптимальной стратегии
.
Аналогично стратегияj
игрока 2 называется его активной
стратегией,
если в оптимальной стратегии
![]() вероятность
вероятность![]() .
.
Теорема 5. Если один из участников игры применяет свою оптимальную стратегию, то ожидаемый выигрыш останется неизменным и равным v независимо от характера действий другого участника игры в пределах его активных стратегий.
Доказательство.
Обозначим
![]() для каждых
для каждых![]() ,
где
,
где![]() – множество оптимальных стратегий
первого игрока;
– множество оптимальных стратегий
первого игрока;![]() для каждых
для каждых![]() ,
где
,
где![]() – множество оптимальных стратегий
второго игрока. Пусть второй игрок
выбрал чистую стратегию
– множество оптимальных стратегий
второго игрока. Пусть второй игрок
выбрал чистую стратегию![]() тогда величина среднего выигрыша будет
равна
тогда величина среднего выигрыша будет
равна![]() .
Данный среднийвыигрыш
достигается в том случае, когда первый
игрок выбирает свою оптимальную стратегию
.
Данный среднийвыигрыш
достигается в том случае, когда первый
игрок выбирает свою оптимальную стратегию
![]() а второй игрок реализует чистую стратегию
из числа активных. Очевидно, что
а второй игрок реализует чистую стратегию
из числа активных. Очевидно, что
![]() .
.
С другой стороны, по определению значение игры будет равно
![]()
Таким образом, получаем систему
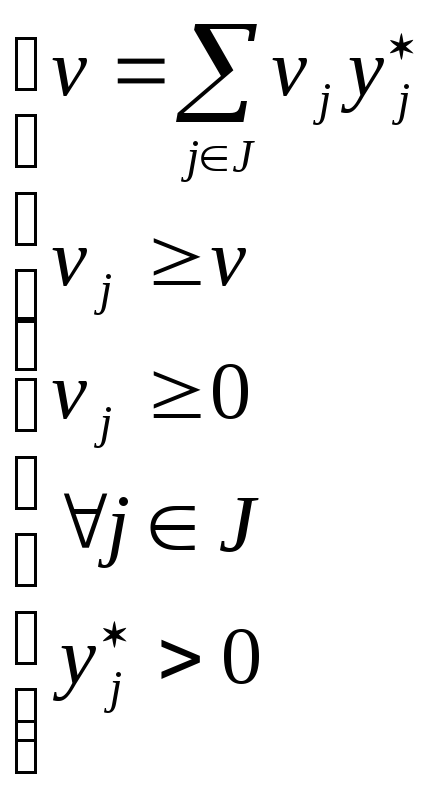
Это условие может выполняться только в случае, когда
![]()
![]()
Теорема доказана.
§2.1.5. Решение игры в смешанных стратегиях
Пусть задана
матричная антагонистическая игра.
Требуется найти решение игры в смешанных
стратегиях, т.е. требуется найти значение
игры v,
оптимальную стратегию первого игрока
![]() оптимальную стратегию второго игрока
оптимальную стратегию второго игрока![]() .
.
Решение. Запишем матрицу игры
|
|
смеш. стр. второго игрока |
|
смеш. стр. первого игрока |
|
Из теоремы об
активных стратегиях (теорема 5) следует,
в частности, что применение одним из
игроков своей оптимальной стратегии
против любой чистой стратегии противника
даёт результат не хуже, чем значение
игры V.
Результат для первого игрока должен
быть
![]() ,
а результат для второго
,
а результат для второго![]() .
Тогда первый игрок решает задачу
нахождения решения
.
Тогда первый игрок решает задачу
нахождения решения![]() ,
удовлетворяющего условиям:
,
удовлетворяющего условиям:
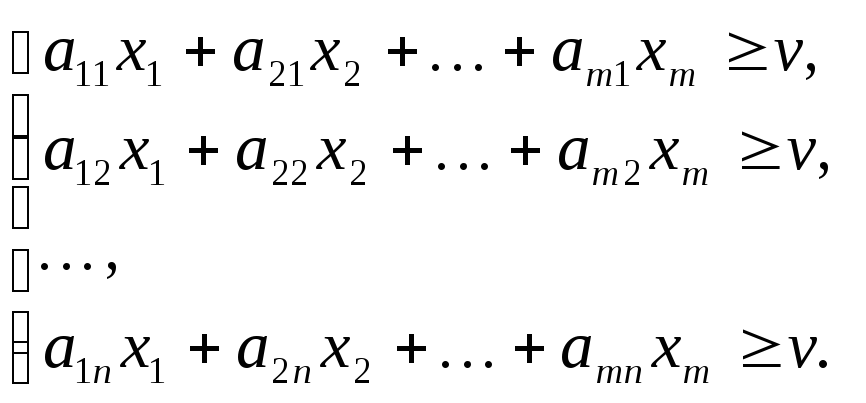 (1.28)
(1.28)
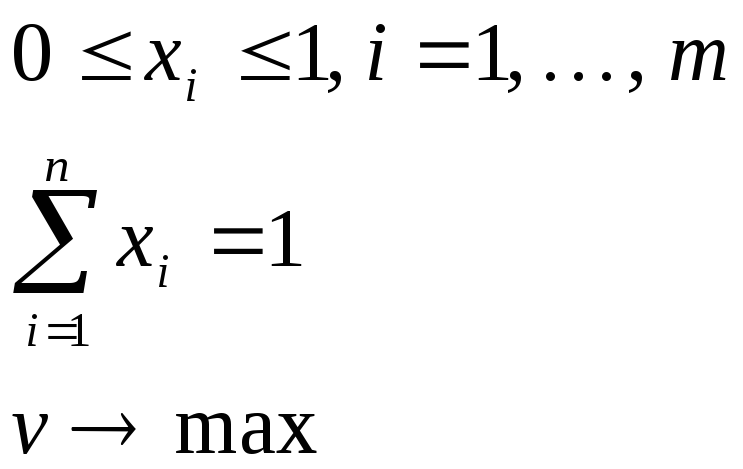
Второй игрок решает
задачу нахождения решения
![]() ,
удовлетворяющего условиям:
,
удовлетворяющего условиям:
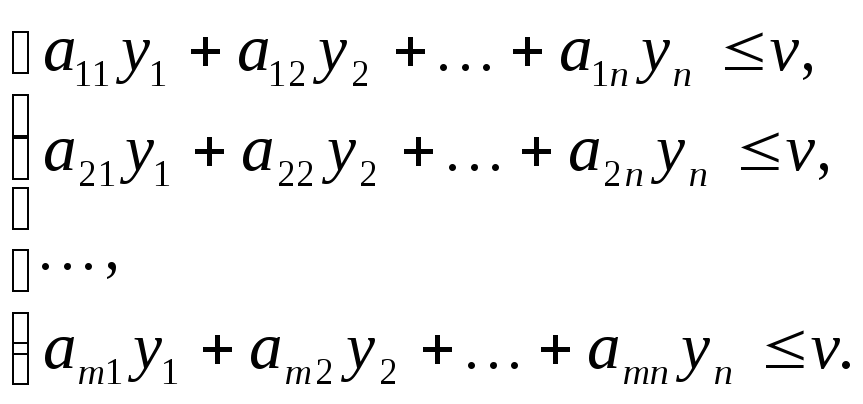 (1.29)
(1.29)
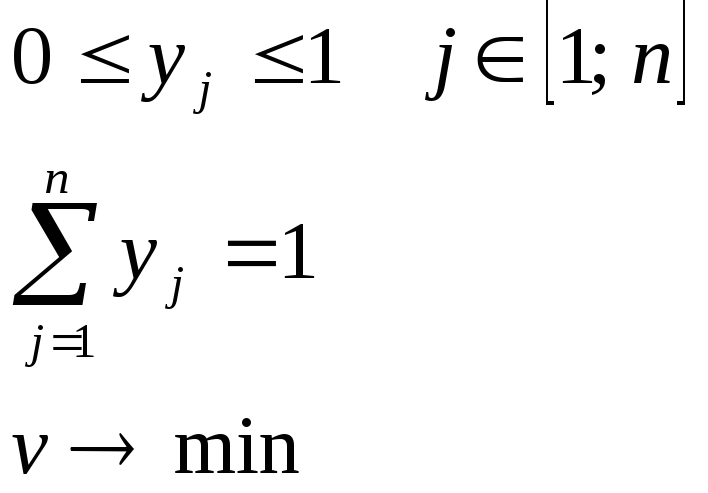
Задачи первого и второго игроков вместе образуют двойственную задачу линейного программирования. Такие задачи решаются с помощью двойственного симплекс-метода. В частности, можно доказать, что сформулированная выше двойственная задача линейного программирования имеет решение для любых платёжных матриц.
Из этого следует,
что любая матрица антагонистической
игры имеет решение в смешанных стратегиях.
Для частного случая, когда матрица игры
имеет размеры
![]() ,
смешанные стратегии можно найти
графическим методом. Действительно,
пусть матричная игра задана Таблицей
6.
,
смешанные стратегии можно найти
графическим методом. Действительно,
пусть матричная игра задана Таблицей
6.
Таблица 6
|
|
смеш. стр. второго игрока |
|
смеш. стр. первого игрока |
|
Сформулируем задачу для первого и второго игроков
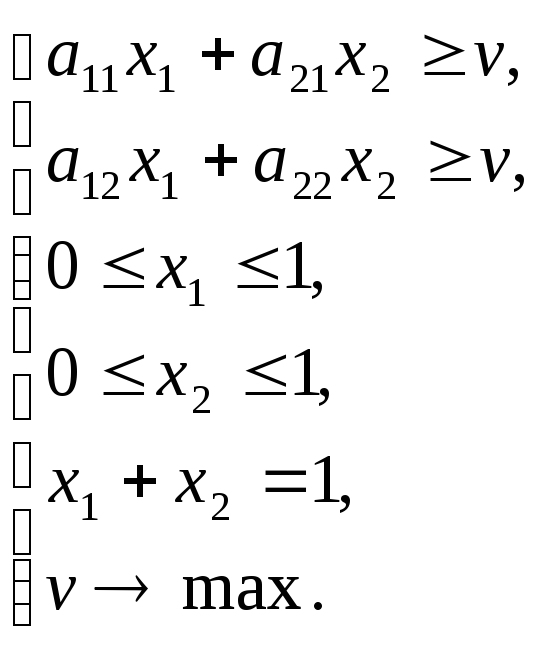 (1.30)
(1.30)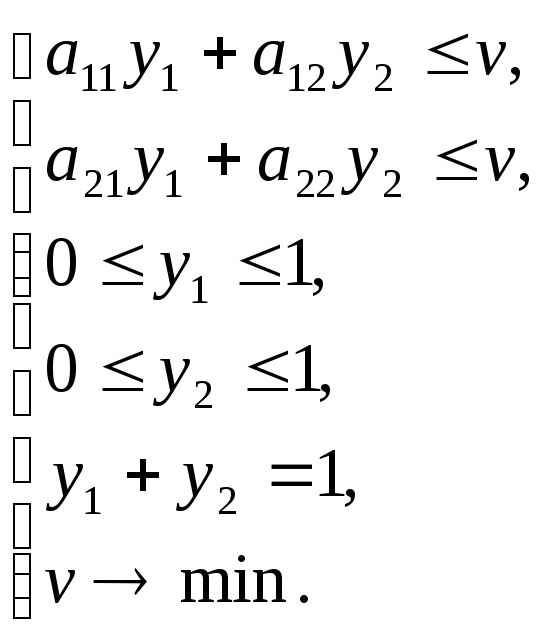 (1.31)
(1.31)
Решим задачу для
первого игрока. Обозначим
![]() тогда
тогда![]()
![]()
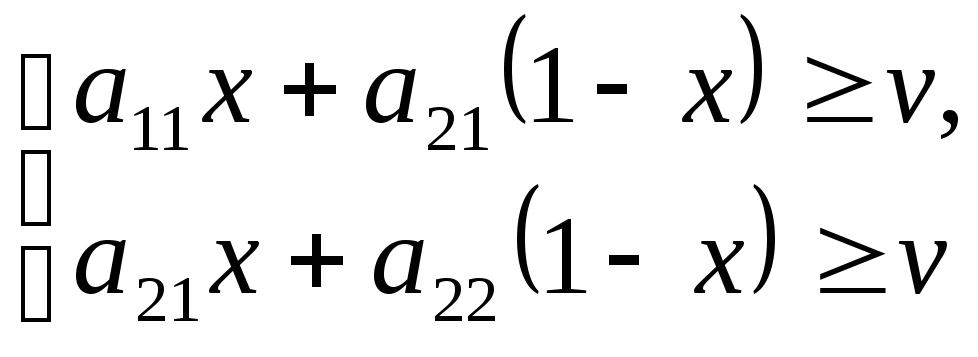
![]()
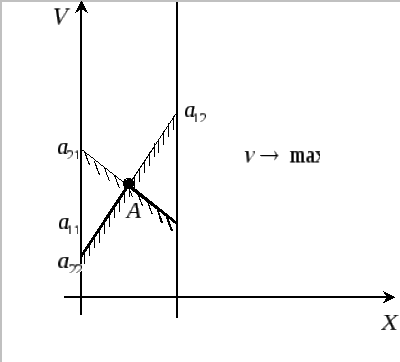
Решим полученную задачу линейного программирования графически в осях v и X (Рис.2):
Рисунок 2
Свойства игры в смешанных стратегиях.
Решение игры не изменится при вычёркивании доминируемых стратегий.
Решение игры не изменится при добавлении доминируемых стратегий.
Решение игры не изменится при перестановке местами строк (столбцов) платёжной матрицы. Т.е. игроки могут нумеровать свои стратегии в любом порядке. Смысл игры и её решение от этого не изменится.
§2.1.6. Игра против природы
Смысл игры против природы состоит не в том, что игрок вредит окружающей среде, и не в том, что природа враждебна игроку, а в том, что игрок выбирает своё решение, не зная состояния внешней среды, от которых зависит его выигрыш, т.е. в условиях неопределённости. Эта неопределённость вызвана внешними случайными факторами – природными, социальными, техническими, политическими, экономическими. Всю совокупность перечисленных случайных факторов принято называть природой (Nature).
Предположим, что
экономический субъект выбирает свои
стратегии из некоторого множества
![]() .
Он знает, что внешний мир (природа),
независимо от его действий, может
находиться в одном из состояний
.
Он знает, что внешний мир (природа),
независимо от его действий, может
находиться в одном из состояний![]() .
Эти состояния можно условно считать
стратегиями природы. Каждое из состояний
природы в сочетании со стратегией
экономического субъекта (игрока) приводит
к определённым исходам. Каждый исход
оценивается игроком в зависимости от
полезности для него этого исхода. Таким
образом, множество исходов и заданная
на них функция полезности экономического
субъекта задают платёжную матрицу с
элементами
.
Эти состояния можно условно считать
стратегиями природы. Каждое из состояний
природы в сочетании со стратегией
экономического субъекта (игрока) приводит
к определённым исходам. Каждый исход
оценивается игроком в зависимости от
полезности для него этого исхода. Таким
образом, множество исходов и заданная
на них функция полезности экономического
субъекта задают платёжную матрицу с
элементами![]() – выигрыш (полезность) экономического
субъекта при выборе им стратегии i
и состоянии
природы j.
– выигрыш (полезность) экономического
субъекта при выборе им стратегии i
и состоянии
природы j.
Следовательно, игра против природы является частным случаем матричной игры. Её особенность состоит в том, что второй игрок (природа) не преследует собственные цели, то есть является безразличным игроком. Стратегии природы являются ее возможными состояниями, определяемыми объективными законами, а также случайными, неизвестными игроку факторами.То, что у природы нет собственных интересов, отнюдь не облегчает задачу принятия решений, потому что в игре против природы нельзя предусмотреть ее стратегии, исходя из ее «интересов». Модели выбора решения в игре против природы делятся на два типа. Во-первых, это модели выбора при определенном критерии оптимальности, применяемые в тех случаях, когда смысл задачи не дает возможности игроку использовать смешанные стратегии. Во-вторых, это модели с использованием смешанных стратегий.