Файл: Теория игр для экономистов doc.doc

Покажем на популярных примерах игровых задач, как с помощью математической модели можно получить ответы на некоторые вопросы.

Пример. «Орел - решка».

Два участника игры подбрасывают по монетке достоинством в 1 рубль. Если на обеих монетах выпадут одинаковые значения (орел-орел или решка-решка), то обе монеты достаются первому игроку. Если значения на монетах различны, то обе монеты достаются второму игроку. Сформулируем вопрос: может ли игрок максимизировать свой выигрыш?

Для ответа на вопрос представим данную конфликтную ситуацию в виде таблицы (Таблица 1), записывая выигрыш первого игрока со знаком «+», а второго со знаком «-».

Таблица 1

Решение. Каждый из четырех исходов в таблице 1 является результатом двух случайных событий – выпадения на двух монетах «орла» или «решки». В силу равновозможности исходов, вероятность каждого из них равна ¼. Выбор стратегии также является случайным и не зависит от воли игрока. В данной игре результат зависит от случая, игроки не имеют возможности влиять на свой выигрыш.

Пример. «Запиши число».

Среди нескольких игроков разыгрывается приз (например, 100 рублей). По правилам игры каждый участник записывает некоторое число от 0 до 10, затем определяется среднее арифметическое всех чисел и делится на 3, полученное число обозначим r. Приз получает тот игрок, чье число имеет наименьшее абсолютное отклонение от r. Если несколько игроков назвали числа, дающие наименьшее отклонение от r. То приз делится между ними поровну. Вопрос: может ли каждый игрок обеспечить себе ненулевой выигрыш? Чем закончится игра, если все игроки будут действовать оптимальным образом?

Решение. Рассмотрим сначала случай, когда число участников игры равно 2. Покажем, что игрок, записавший число 0, получит выигрыш не меньший 50.

Действительно, если другой игрок также запишет 0, то 100 делится пополам, каждый получает 50. Если же другой игрок запишет число x>0, то r=x/6. Для игрока, записавшего 0, абсолютное отклонение r от 0 составит x/6, а для игрока, записавшего x, отклонение составит |(x- r )/6|=5x/6. Приз в 100 рублей получит игрок, записавший 0. Если оба игрока абсолютно рациональны, то они выберут свои оптимальные стратегии¹, т.е. запишут 0, тогда исходом игры будет получение каждым игроком 50 рублей.

Если число игроков равно 3, то число 0 не будет оптимальной стратегией. Например, если первый игрок запишет 0, второй 1, а третий 9, то выигрыш получит второй игрок. Точно также оптимальными не будут все остальные числа, т.к. против любого числа x, записанного первым игроком, найдутся числа y и z, записанные другими игроками, для которых абсолютное отклонение x от r будет больше чем отклонение от r числа y или z. Следовательно, исход игры является неопределенным.

Пример. «Дилемма заключенных».

Два человека совершили общее преступление, т.е. являются сообщниками. Их задержали по подозрению, но следствие не имеет явных доказательств их вины, поэтому им предложили помогать следствию. Они получат по 4 года заключения, если оба сознаются в совершении преступления. Они получат по 2 года заключения, если ни один из них не сознается (предполагается, что в этом случае следствие не сможет им предъявить полноценного обвинения, но в некоторых правонарушениях их все же обвинят). Если один из них сознается, а другой не сознается, то сознавшийся получит 1 год заключения за содействие правосудию, а не сознавшийся - 7 лет. Подозреваемые не имеют возможности передавать друг другу информацию. Какие решения склонны принимать заключенные, если они стремятся получить наименьший срок заключения, и при этом не принимают в расчет этические принципы, такие как солидарность, честность и взаимное доверие.

Решение. Представим данную конфликтную ситуацию в виде таблицы, где каждый возможный исход находится в клетке на пересечении стратегий 1-го и 2-го заключенного, и характеризуется «выигрышами» обоих заключенных. (Таблица 2). и в виде дерева решений (Таблица 3). «Выигрыши» игроков обозначим как количество лет заключения, взятое по очевидным причинам со знаком «-».

Таблица 2

Ту же информацию можно представить в виде «дерева решений» (Таблица 3).

Таблица 3

Анализ Таблицы 2 и Таблицы 3 показывает, что при любой стратегии 2-го заключенного для 1-го заключенного выбор стратегии «сознаваться» дает лучший результат, чем выбор альтернативной стратегии («не сознаваться»). Как мы покажем позднее, такая стратегия называется доминирующей. То же справедливо и для 2-го заключенного. Следовательно, исходом, оптимальным выбором обоих заключенных будет стратегия «сознаться», следствием чего будет исход, при котором они получат по 4 года заключения. В то же время, лучший результат они получили бы при одновременном выборе стратегии «не сознаться». Однако, несогласованность действий мешает реализации этого исхода: каждому заключенному в отдельности хочется сократить срок заключения и они отказываются от стратегии «не сознаваться», которую они выбрали бы при условии согласованности действий. Заметим, что условие, мешающее им общаться, не очень существенно. Даже, если бы заключенные могли переписываться и договориться, что они не будут сознаваться, это не гарантировало бы выбор стратегии «не сознаваться», потому что каждому в отдельности выгоднее лот нее отказаться. Чтобы оба участника следовали этой стратегии, в правила игры надо ввести изменения: либо предполагать, что заключенные абсолютно доверяют друг другу, либо ввести штрафные санкции за отказ от стратегии «не сознаваться», либо (как это будет сделано в последующих главах), предполагать, что игровая ситуация разыгрывается неограниченное число раз. Но это, разумеется, потребует построения другой математической модели.

Пример. «Красный тигр».

Число участников равно 2. Первый игрок называет одного из двух животных – «тигр» или «обезьяна». Второй участник называет один из трех цветов – «желтый», «красный», «черный». Выигрыши игроков для всех возможных исходов указаны в Таблице 4 (первое число – выигрыш 1-го, второе число – выигрыш 2-го игрока).

Таблица 4

Попытаемся ответить на вопрос, имеют ли игроки стратегии, которые обеспечивают им значение выигрыша, которое не может стать меньше при любых действиях соперника.

Решение. Анализ таблицы 4 показывает, что среди стратегий 2-го игрока есть стратегия, которой ему невыгодно пользоваться. В самом деле, сравним стратегии «красный» и «черный». Если первый игрок применит стратегию «обезьяна», то стратегия «черный» окажется хуже, чем стратегия «красный (-2 против 1). Если первый игрок применит стратегию «тигр», будет иметь место тот же вывод (-1 против 0). Предполагая, что 2-й игрок рационален, 1-й игрок поймет, что стратегия «черный» не будет применяться, следовательно, останется таблица из двух строк и двух столбцов. Сравним стратегии 1го игрока «тигр» и «обезьяна» по первым двум столбцам. При использовании 2-м игроком стратегии «желтый», стратегия «тигр» лучше стратегии «обезьяна» (2 против -2). То же при стратегии «красный» (1 против 0).

§1.2. Формальное описание игры.

Для формального описания игры (конфликта) необходимо зафиксировать следующие моменты:

1. Множество участников, т.е. тех сторон, которые участвуют в конфликте, имеют свои интересы и принимают решения, от которых зависит исход конфликта; будем считать, что число участников счётное (может быть пронумеровано). Иногда заинтересованные лица и лица, принимающие решения могут не совпадать. В дальнейшем будем называть каждого, кто принимает решения, влияющие на исход игры, игроком.

2. Возможные действия участников – стратегии. Каждый участник (игрок) может выбирать своё действие (стратегию или ход) из некоторого множества доступных ему действий.

Будем обозначать:– множество стратегий 1-го участника;

–множество стратегий 2-го участника;

–множество стратегий n-го участника.

Первый участник, независимо от остальных, выбирает стратегию второй –…,n-ый – . Результат этих независимых выборов можно истолковать как определенную ситуацию x={s₁, s₂,…s_n}, называемую исходом игры.

Обозначим всё множество исходов . Очевидно, что это множество исходовбудет равно декартову произведению множеств .

=

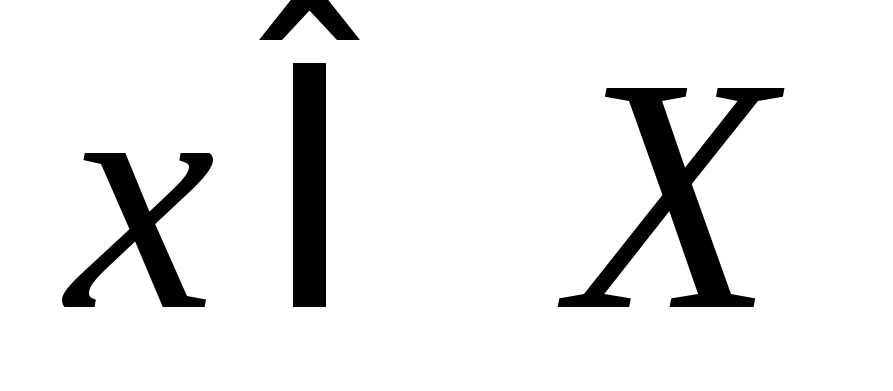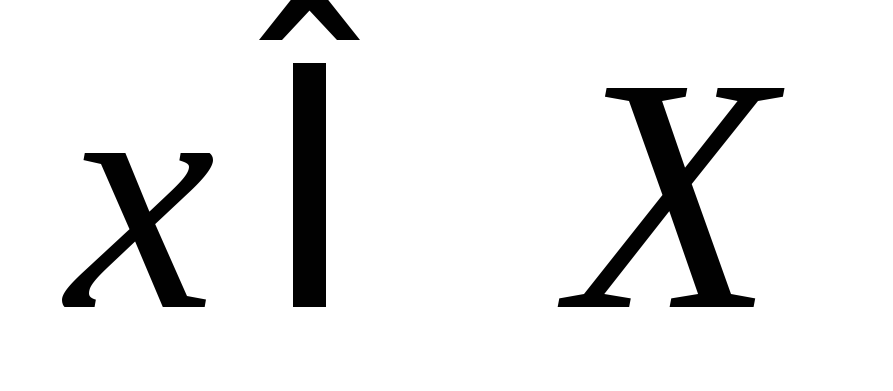3. Каждый исход приводит к определённымпоследствиям для каждого участника. Будем считать, что эти последствия можно выразить количественно и будет называть соответствующее числовыигрышем участника, т.о. будет соответствовать набор чисел: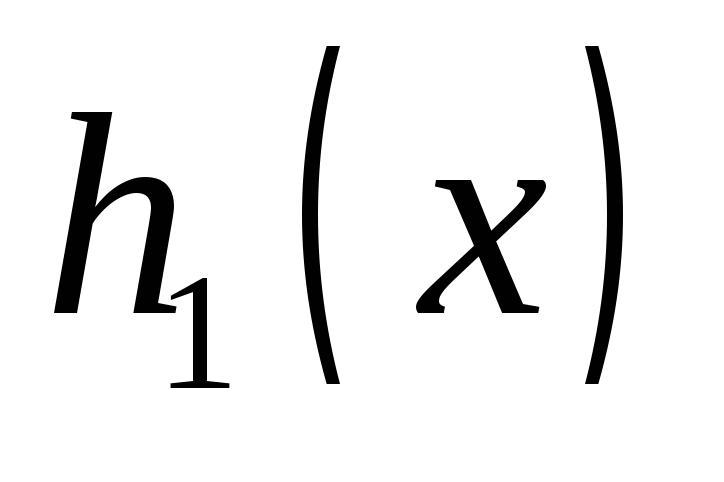– выигрыш 1-го участника;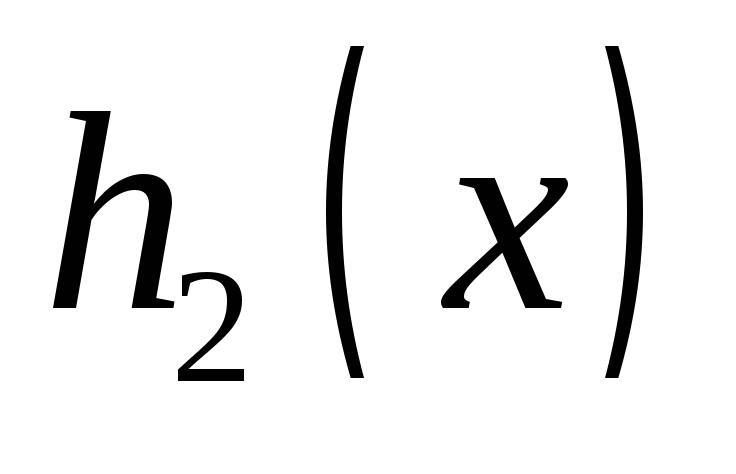– выигрыш 2-го участника;