ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.08.2024
Просмотров: 360
Скачиваний: 0
СОДЕРЖАНИЕ
§1.2. Формальное описание игры.
§2.1.1. Понятие антагонистической игры. Матричная игра.
§2.1.2. Доминирование стратегий. Редукция игры. Решение игры в доминирующих стратегиях.
§2.1.3. Решение игры в чистых стратегиях
§2.1.4. Смешанное расширение игры
§2.1.5. Решение игры в смешанных стратегиях
Свойства игры в смешанных стратегиях.
§2.1.7. Критерии оптимальности решения в условиях неопределённости
§2.1.9. Критерий Вальда (максиминный критерий)
§2.1.10. Критерий Гурвица (критерий взвешенного оптимизма /пессимизма)
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
§2.1.12. Решение игры против природы в смешанных стратегиях
§ 2.2 Неантагонистические игры
§2.2.1. Понятие неантагонистической игры
§2.2.4. Эффективность по Парето2
§2.2.5. Повторяющиеся игры. Применение к микроэкономике.
Глава 3. Кооперативные решения
§3. 1. Понятие коалиционной игры
§3.2. Определение решения игры
§3.3. Эффективность обмена. Ящик Эджворта
Практикум Матричная игра. Доминирование стратегий.
Решение игры в чистых стратегиях.
Решение игры в смешанных стратегиях.
Игра против природы. Критерии Лапласа, Вальда, Сэвиджа, Гурвица.
Очевидно, что если α = 1, то критерий Гурвица превращается в критерий Вальда.
Докажем, что критерий Гурвица удовлетворяет принципу доминирования.
Доказательство. Пусть стратегия xi является доминирующей. Это значит, что для всех j, 1 ≤ j ≤ n и для всех k, 1 ≤ k ≤ m, k ≠ j, выполняется неравенство:
f(xi,yj) ≥ f(xk,yj). (1.34)
Из этого следует, что:
max f(xi,yj) ≥ max f(xk,yj). (*)
Докажем выполнение неравенства (*) подробнее:
max f(xi,yj) = f(xi,yp)
max f(xk,yj) = f(xk,yq)
f(xi,yj) ≤ f(xi,yp)
f(xk,yj) ≤ f(xk,yq)
Из (1.34) следует, что f(xk,yq) ≤ f(xi,yq) ≤ f(xi,yp).
Таким образом, получается bk ≤ bi.
Введём обозначения: min f(xi,yj) = аi = f(xi,yl),
min f(xk,yj) = ak = f(xk,yr)
Из неравенства доминирования (d) следует, что f(xk,yp) ≤ f(xi,yr)
аi = f(xi,yl) ≥ f(xk,yl) ≥ min f(xk,yl) = ak
аi ≥ ak
Так как α ≥ 0, 1- α ≥ 0, то:
α * аi ≥ α * аk
(1- α)* bi ≥ (1- α)* bk
Выполнение условий перестановки и аддитивной постоянной достаточно очевидно.
Недостаток критерия Гурвица: недостаточная обоснованность выбора параметра α (его значение основано на оценке отношения ЛПР к риску).
§2.1.11. Критерий Сэвиджа (критерий наименьших сожалений)
Критерий основан на гипотезе, что ЛПР предпочитает такое решение, при реализации которого у него возникают наименьшие сожаления.
Рассмотрим матричные игры, заданные Таблицей 1.
Если ЛПР думает, что среда примет какое-то определенное состояние yj, он выберет стратегию, максимизирующую его выигрыш при данном состоянии среды yj, Обозначим соответствующую стратегию xl , тогда очевидно, что для всех стратегий xi справедливо неравенство
f(xl,yj) ≥ f(xi,yj),
другими словами f(xl,yj) – наибольший элемент в столбце j.
Следовательно, для любого столбца j и любой строки i разность
rij= f(xl,yj)- f(xi,yj)
является неотрицательным числом и показывает потерю выигрыша ЛПР, если он выберет стратегию xi, а среда примет состояние yj.
Итак, критерий Сэвиджа даёт следующий алгоритм выбора наилучшего решения:
для всех yj находят наилучшее решение для данного состояния:
сj = max f(xi,yj)
для каждого исхода xi для всех yj находят значение потерь или сожалений:
rij = сj - f(xi,yj)
получают матрицу потерь:
R = || rij ||
4) для каждой альтернативы находят наибольшее сожаление:
Si = max rij
решаем задачу нахождения хk:
Sk ≤ Si
minmax rij
Пример: Найти решение оптимальное по критерию Сэвиджа для матрицы Таблица 11:
Таблица 11
|
|
у1 |
У2 |
у3 |
у4 |
у5 |
|
х1 |
1 |
3 |
2 |
4 |
5 |
|
х2 |
0 |
6 |
8 |
7 |
9 |
|
maxi |
0 |
6 |
8 |
7 |
9 |

 1-1 6-3 8-2 7-4 9-5
1-1 6-3 8-2 7-4 9-5
cij=
1-0 6-6 8-8 7-7 9-9

 0 3 6 3 4 6
0 3 6 3 4 6
cij=
1 0 0 0 0 1
max cij = 6 – наибольшее сожаление.
Можно показать, что критерий Сэвиджа удовлетворяет принципу доминирования, инвариантности при перестановке, инвариантности при добавлении аддитивной постоянной.
Критерий Сэвиджа отличается от критерия Вальда тем, что для критерия Сэвиджа реализуется принцип minmax для матрицы потерь, а для критерия Вальда - maxmin для матрицы выигрышей.
§2.1.12. Решение игры против природы в смешанных стратегиях
Критерии Вальда, Лапласа, Гурвица, Сэвиджа применяются в тех случаях, когда ЛПР вынужден выбирать только чистые стратегии, и не может использовать смешанные стратегии. Однако, существуют практические задачи принятия решений, в которых ЛПР может применять смешанные стратегии. Рассмотрим два примера таких задач.
Пример. «Задача о зонтике». Природа может реализовать одно из двух состояний: дождь, ясно. Человек принимает одно из двух решений: брать зонт, не брать зонт. Полезности игрока записаны в следующей Таблице 12:
|
Природа
Человек |
Дождь |
Ясно |
|
Брать зонт |
1 |
0 |
|
Не брать зонт |
-1 |
2 |
Предполагается, что решение принимается каждый день. Требуется найти решение в смешанных стратегиях.
Решение. Запишем матрицу
|
|
![]()
Так как
![]() ,
то решения в чистых стратегиях нет.
Найдём решение в смешанных стратегиях.
Рассмотрим задачу для первого игрока.
,
то решения в чистых стратегиях нет.
Найдём решение в смешанных стратегиях.
Рассмотрим задачу для первого игрока.
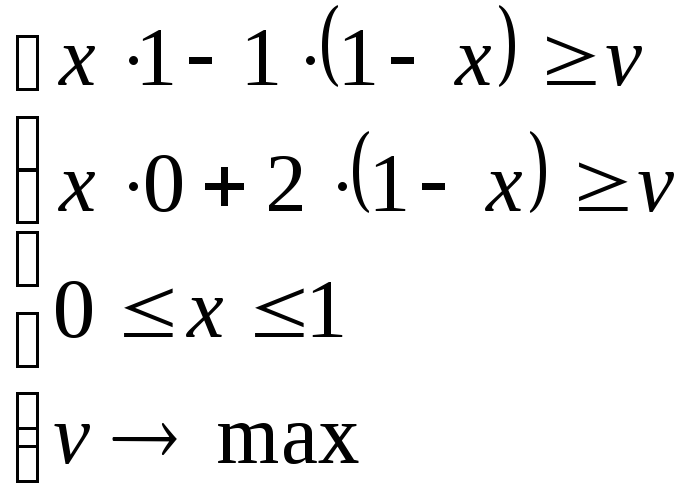
Графо-аналитическое решение (Рис.3):
![]()
Рисунок 3
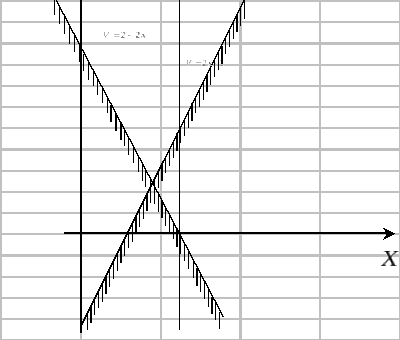
![]()
![]()
![]()
![]()
Ответ: в трёх случаях из четырёх нужно брать зонт.
Пример.«Комплектация
оборудования».
Фирма выбирает между несколькими типами
комплектации оборудования. Стратегиями
фирмы в комплектации оборудования будут
![]() .
.
Внешняя среда
(заказчики) выбирают тип заказа. Каждому
типу комплектации и каждому типы заказа
соответствует определённый исход,
который приносит фирме прибыль (убыток)
![]() .
В результате получаем матрицу игры
Таблица 12:
.
В результате получаем матрицу игры
Таблица 12:
Таблица 12
|
Типы заказов |
|
||||||||||||||
|
|
1 |
2 |
… |
j |
… |
n |
|
||||||||
|
Типы комплектации |
1 |
|
|
… |
|
… |
|
||||||||
|
2 |
|
|
… |
|
… |
|
|||||||||
|
|
|
|
… |
|
… |
|
|||||||||
|
|
|
|
… |
|
… |
|
|||||||||
|
|
… |
… |
… |
… |
… |
… |
|||||||||
|
m |
|
|
… |
|
… |
|
|||||||||