ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 15.04.2024
Просмотров: 507
Скачиваний: 0
СОДЕРЖАНИЕ
Ваш репетитор: Филимонова л.В.
1.6.3 Движение под углом к горизонту …………………………....33
Общие методические рекомендации по решению задач
Движение под действием силы тяжести
Движение под углом к горизонту
Прямолинейное движение под действием нескольких сил
Движение связанных тел с использованием блоков
Движение по горизонтальной плоскости
Движение по наклонной плоскости
Действие сил при вращательном движении
Комплексные задачи повышенной трудности
Работа и энергия. Работа внешних сил и ее связь с изменением энергии. Мощность.
Кинетическая энергия при вращательном движении материальной точки
Энергия упруго деформированного тела
Механический импульс и закон сохранения импульса
Взаимосвязь законов сохранения импульса и энергии
Комплексные задачи повышенной трудности
С горизонтальной поверхности земли бросили мяч и он упал на землю со скоростью V= 9,8 м/с по углом= 300к горизонту. Модуль вертикальной составляющей скорости в точке бросания был на 20% больше, чем в точке падения. Найти время полета мяча. Считать, что сила сопротивления движению мяча пропорциональна его скорости.[
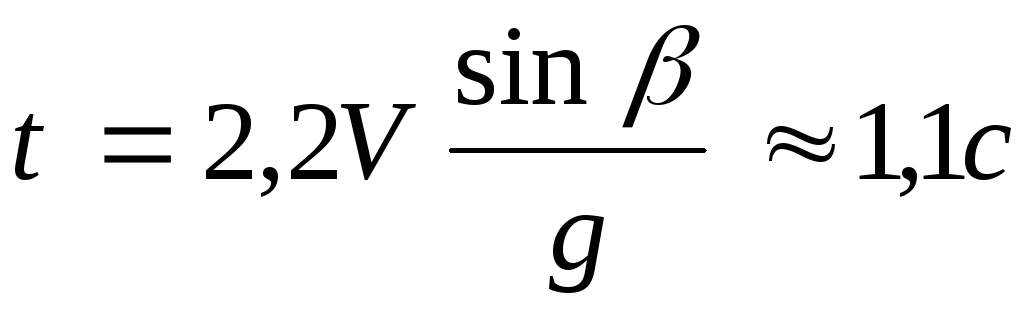 ]
]З
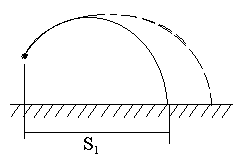 а
время полета мяча, брошенного под углом
к горизонту, горизонтальная составляющая
его скорости уменьшилась на 12% и мяч
упал на землю на расстоянии 14 м от
человека. Когда мяч бросили под тем же
углом к горизонту со скоростью на 20%
большей, чем в первом случае, то
горизонтальная составляющая скорости
мяча за время полета уменьшилась на
15%. На каком расстоянии от человека упал
в последнем случае мяч? Считать, что
сила сопротивления движению мяча
пропорциональна его скорости. [S2= 1,5S1= 21 м]
а
время полета мяча, брошенного под углом
к горизонту, горизонтальная составляющая
его скорости уменьшилась на 12% и мяч
упал на землю на расстоянии 14 м от
человека. Когда мяч бросили под тем же
углом к горизонту со скоростью на 20%
большей, чем в первом случае, то
горизонтальная составляющая скорости
мяча за время полета уменьшилась на
15%. На каком расстоянии от человека упал
в последнем случае мяч? Считать, что
сила сопротивления движению мяча
пропорциональна его скорости. [S2= 1,5S1= 21 м]М
 яч,
брошенный с горизонтальной поверхности
земли под углом 600к горизонту со
скоростью 10 м/с, упал на землю, имея
вертикальную составляющую скорости
по абсолютной величине на 30% меньше,
чем при бросании. Найти время полета
мяча. Считать, что сила сопротивления
движению мяча пропорциональна его
скорости.[
яч,
брошенный с горизонтальной поверхности
земли под углом 600к горизонту со
скоростью 10 м/с, упал на землю, имея
вертикальную составляющую скорости
по абсолютной величине на 30% меньше,
чем при бросании. Найти время полета
мяча. Считать, что сила сопротивления
движению мяча пропорциональна его
скорости.[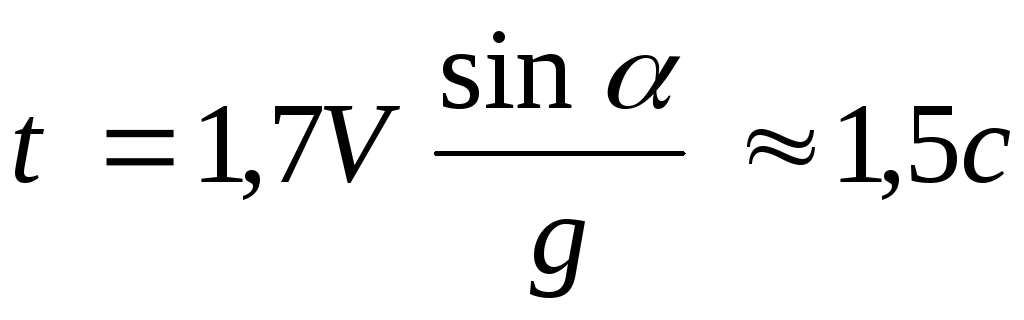 ]
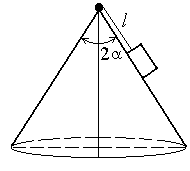
]К вершине прямого кругового конуса прикреплена небольшая шайба с помощью нити длиной l. Вся система вращается вокруг оси конуса, расположенной вертикально. При каком числе оборотов в единицу времени шайба не будет отрываться от поверхности конуса? Угол при вершине конуса 2= 1200.
Ш
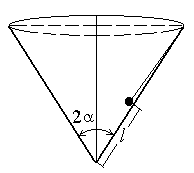 арик
массыmподвешен на нити длинойl.
Его отклонили от положения равновесия
до высоты точки подвеса и отпустили.
При каком значении угла(угол между нитью и вертикалью) нить
оборвется, если известно, что нить
выдерживает удвоенный вес шарика?
арик
массыmподвешен на нити длинойl.
Его отклонили от положения равновесия
до высоты точки подвеса и отпустили.
При каком значении угла(угол между нитью и вертикалью) нить
оборвется, если известно, что нить
выдерживает удвоенный вес шарика?Воронка в виде прямого кругового конуса с углом 2 = 1200при вершине вращается вокруг своей оси, расположенной вертикально. К краю воронки прикреплен с помощью нити небольшой шарик на расстоянииlот вершины конуса. С каким максимальным периодом должна вращаться система, чтобы нить не провисала при таком положении шарика?
Часть третья: Статика
Основные термины и уравнения
В статике выделяются 2 условия равновесия тел.
Первое условие равновесия– векторная сумма всех сил действующих на тело равна нулю:
![]() (3.1)
(3.1)
Векторное равенство (3.1) равносильно системе трех скалярных равенств, получаемых из него проектированием на координатные оси. Иногда на практике достаточно плоской координатной системы и соответствующей системы всего лишь двух равенств-проекций.
М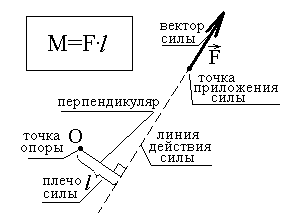 оментом
силы относительно точки О
называется физическая величина, равная
векторному произведению вектора силы
и радиус вектора точки приложения этой
силы (рис.):
оментом
силы относительно точки О
называется физическая величина, равная
векторному произведению вектора силы
и радиус вектора точки приложения этой
силы (рис.):
![]() .
Направление вектора
.
Направление вектора![]() совпадает
с направлением поступательного движения
правого винта при его вращении от
совпадает
с направлением поступательного движения
правого винта при его вращении от
![]() к
к
![]() ,
а модуль равен:
,
а модуль равен:
![]() (3.2)
(3.2)
Т.е. момент силы
![]() –
векторная физическая величина. Часто
при решении задач моментом силы называют
лишь числовое значение вектора
–
векторная физическая величина. Часто
при решении задач моментом силы называют
лишь числовое значение вектора![]() ,
т.е. скалярную положительную величину
,
т.е. скалярную положительную величину![]() ,
тогда говорят: момент силы равен
произведению модуля этой силы на ее
плечо. Как момент силы, так и плечо силы
берутся относительно некоторой выделенной
точки О (точка опоры).Плечом силы
относительно точки О называется
кратчайшее расстояние от этой точки до
линии действия этой силы.Как известно
из математики, кратчайшее расстояние
от точки до прямой есть длина перпендикуляра,
опущенного из этой точки на прямую.
,
тогда говорят: момент силы равен
произведению модуля этой силы на ее
плечо. Как момент силы, так и плечо силы
берутся относительно некоторой выделенной
точки О (точка опоры).Плечом силы
относительно точки О называется
кратчайшее расстояние от этой точки до
линии действия этой силы.Как известно
из математики, кратчайшее расстояние
от точки до прямой есть длина перпендикуляра,
опущенного из этой точки на прямую.
При этом направление момента силы заменяют знаком «+» (если сила стремиться повернуть тело относительно точки опоры против (по) часовой стрелки) или «» (в противном случае). Тогда сложение векторов моментов сил сводится к нахождению соответствующей алгебраической (т.е. с учетом знака) суммы их числовых значений.
Второе условие равновесия – алгебраическая сумма моментов всех сил, действующих на тело, относительно какой-либо точки а равна нулю:
![]() (3.3)
(3.3)
Методические указания. Надлежащий выбор точки А обеспечивает уменьшение количества неизвестных данных в уравнении за счет того, что момент неизвестной силы относительно выбранной точки равен нулю. В частности, например, если точка А лежит на линии действия этой силы.
Среди задач можно выделить несколько групп:
задачи, которые решаются только по первому условию равновесия (например, брусок покоится на столе, т.е. вращение здесь невозможно);
задачи, которые решаются только по второму условию равновесия (задача- пример 2);
задачи, которые могут быть решены на основе только первого условия равновесия, и также на основе только второго условия равновесия (задача-пример 4);
4) задачи, которые решаются при совместном использовании двух условий равновесия.
Примеры решения задач
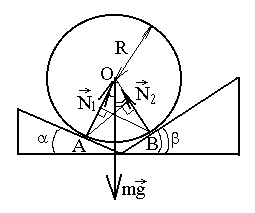
Задача-пример 1. Две треугольные призмы касаются ребрами, при которых углы между гранями равны соответственно и . Сверху на них положили шар радиуса R массой m (рис). Определить силы, с которыми шар действует на каждую призму.
Р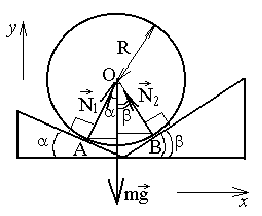 ешение.I-й способ. Записываем первое условие
равновесия шара:
ешение.I-й способ. Записываем первое условие
равновесия шара:![]()
Проектируем его на оси.
х:![]() ;
;
y:![]() .
.
Получили два уравнения с двумя
неизвестными. Обратите внимание, что
каждое уравнение содержит две переменные
N1иN2.
ВыразимN2из
первого уравнения и подставим во второе:![]() ,
,
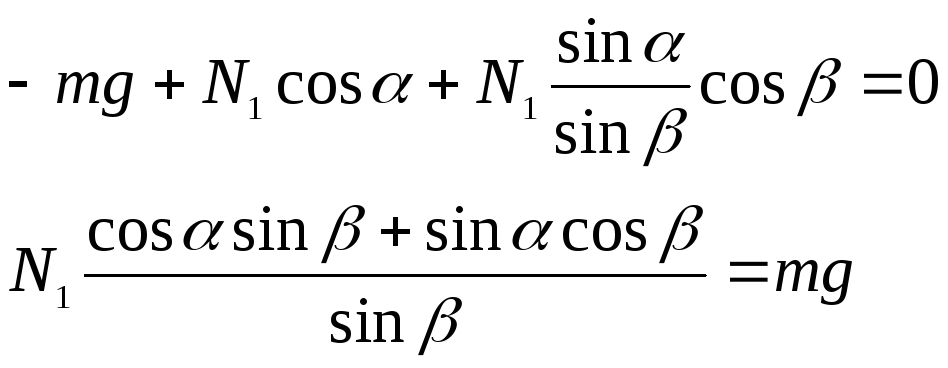
![]() ,
,
аналогично получаем
![]() .
.
II-й способ. Записываем второе условие
равновесия шара относительно точек
опоры А и В. Учтем, что момент силыN1относительно точки А равен нулю, а момент
силыN2относительно точки В равен нулю. Получаем
в скалярной форме два равенства
соответственно:![]()
Видим, что полученные равенства являются уравнениями лишь с одной переменной. Откуда выражаем искомые величины.
Ответ:
![]() ,
,![]() .
.
Задача-пример 2.Один конец твердого стержня массой m шарнирно закреплен в точке А, а другой удерживается веревкой ВС? Найти натяжение веревки, если треугольник АВС равносторонний.
Р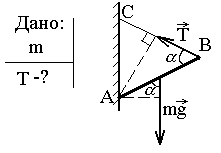 ешение.
На стержень действуют три силы: сила
тяжести, сила натяжения веревки и сила
реакции
ешение.
На стержень действуют три силы: сила
тяжести, сила натяжения веревки и сила
реакции![]() шарнира в точке А. Направление последней
из них на начальном этапе решения
определить невозможно (его можно
рассчитать!). Поэтому первое условие
равновесия использовать для решения
задачи не представляется возможным
из-за неизвестности проекций этой силы.
шарнира в точке А. Направление последней
из них на начальном этапе решения
определить невозможно (его можно
рассчитать!). Поэтому первое условие
равновесия использовать для решения
задачи не представляется возможным
из-за неизвестности проекций этой силы.
Определить плечо силы
![]() относительно какой-либо точки нельзя
не зная линии действия этой силы (по
определению плеча). Однако если мы в
качестве точки опоры возьмем точку А и
учтем, что сила
относительно какой-либо точки нельзя
не зная линии действия этой силы (по
определению плеча). Однако если мы в
качестве точки опоры возьмем точку А и
учтем, что сила![]() приложена в точке А (т.е. линия ее
действия проходит через эти точку), то
плечо силы
приложена в точке А (т.е. линия ее
действия проходит через эти точку), то
плечо силы![]() будет равно нулю, а значит и равен будет
нулю ее момент. Тогда второе условие
равновесия запишется так:
будет равно нулю, а значит и равен будет
нулю ее момент. Тогда второе условие
равновесия запишется так:![]() ,
по рисунку из геометрических соображений
определяем плечи сил и получаем равенство:
,
по рисунку из геометрических соображений
определяем плечи сил и получаем равенство:![]() ,
откуда
,
откуда![]() .
.
Ответ: mg/2.