Файл: Методичка по механике вся Печать новый вариант12г.doc

Полная механическая энергия – сумма кинетической и потенциальной энергии тела:(4.7).

Методические указания. Потенциальная энергия всегда относится к двум или более телам, т.к. для ее наличия необходимо их взаимодействие друг с другом. Когда же речь идет о потенциальной энергии одного конкретного тела, то надо понимать это как энергию ЕГО взаимодействия, но с каким-то другим телом. Если же потребуется найти полную механическую энергию, к примеру, двух тел с учетом их взаимодействия, то получим формулу:

(4.7*).

Известно, что значение потенциальной энергии зависит от конфигурации системы взаимодействующих тел, т.е. от их взаимного расположения, и меняется при переходе системы от одной конфигурации к другой. Поэтому в ходе любого опыта можно измерить только изменение потенциальной энергии. И лишь принимая (совершенно произвольно) значение потенциальной энергии при каком-то взаимном расположении участников взаимодействия за ноль, становится возможным говорить об абсолютном значении потенциальной энергии. Иначе говоря, при анализе физических процессов (в ходе решения задач) важно не само значение потенциальной энергии тела, а величина ее изменения в этих процессах, а чаще всего будет рассматриваться убыль потенциальной энергии. С точки зрения математики термины «изменение» и «убыль» противоположны по знаку: изменение функции равно разности ее конечного и начального значений, а ее убыль равна разности начального и конечного значений. Это необходимо четко различать при формулировке и записи нижеследующих формул.

Теорема о кинетической энергии: изменение кинетической энергии системы равно работе всех внешних сил. Имеем:

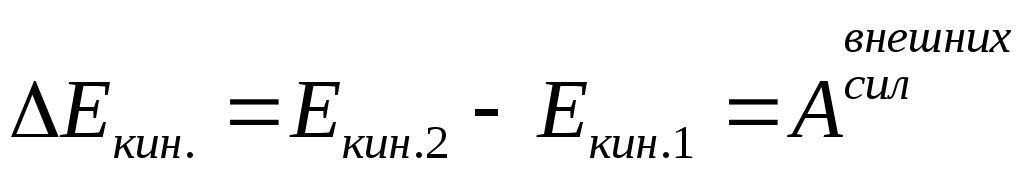(4.8).

Работа потенциальных сил равна убыли потенциальной энергии:

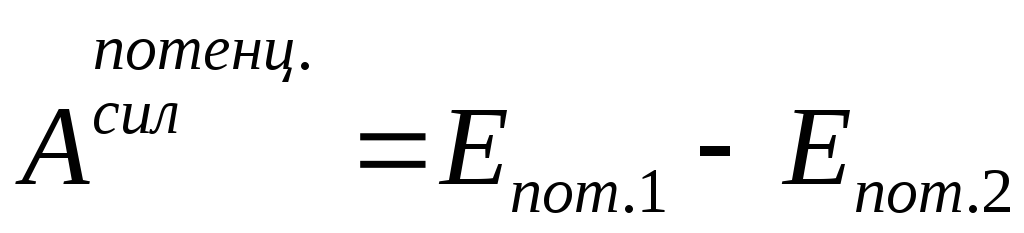(4.9).

И как следствие формул (4.8) и (4.9) получаем закон изменения полной механической энергии:

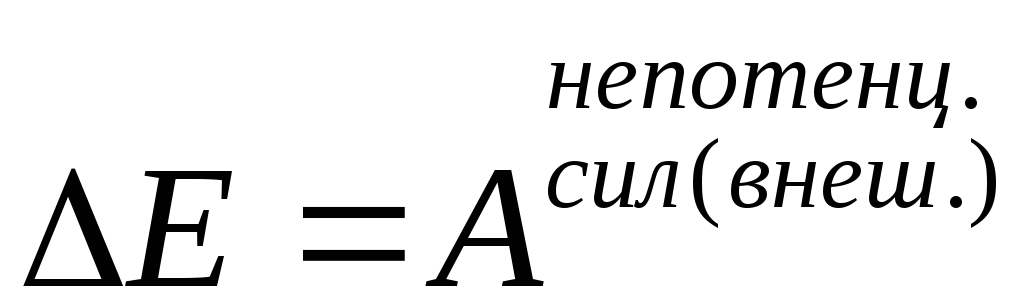(4.10).

Методические указания. При решении задач надо помнить, что изменить полную механическую энергию тела (или системы тел) может работа сил трения, сопротивления и др. (внешняя приложенная сила и т.д.). При их отсутствии имеем дело с так называемым законом сохранения полной механической энергии тела, который записываем в форме: -энергии в любых двух состояниях равны (4.11). И далее с учетом конкретного условия задачи расписываем левую и правую части этого равенства, не выходя за его пределы. Таким образом, оговорки в условии «силу сопротивления не учитывать» или «трением пренебречь» напоминают о возможности использования формулы (4.11).

Обратим внимание на тот факт, что силы трения всегда способствуют переходу энергии из механической во внутреннюю. Поэтому к ним нельзя применять разделение на «внутреннее» трение и «внешнее», т.е. силы трения всегда считаются внешними по отношению к механической системе силами. Потери механической энергии наблюдаются и при процессах с остаточными деформациями (например, неупругий удар).

Любой закон сохранения – это утверждение о том, что какая то величина не меняется в некотором процессе, то есть остается одинакова при переходе из начального состояния системы в конечное.

Чтобы понять смысл, необходимо исходить из закона изменения данной величины. Если нет причин, меняющих величину, то она будет сохраняться.

И поэтому записывается в виде: Х₁=Х₂. Здесь Х – сохраняемая величина.

Однако это утверждение должно быть обосновано! А это уже серьезнее…

Закон сохранения полной механической энергии тела при его переходе из одного положения в другое выполняется (имеет место) в следующих случаях:

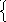
1) непотенциальные силы отсутствуют;

2) непотенциальные силы есть, но их работа равна нулю.

В частности, сохранение механической энергии допускает переход ее из одного вида (потенциальной или кинетической) в другой, но только в равных количествах!

Размерности работы и энергии одинаковы: [A] = [E] =Дж, и совпадают с размерностью другой физической величины – количество теплоты - количественной характеристики процесса теплообмена. Отсюда можно сделать вывод, что работа и теплота – два различных способа изменения энергии тела (или системы). Этот важный для понимания момент отражен и в первом начале термодинамики.

Приведем формулы для подсчета количества теплоты в разных тепловых процессах:

1) нагревание (охлаждение): (4.12), где- теплоемкость тела (Дж/К),- удельная теплоемкость вещества (Дж/(кгК)),- изменение температуры;

2) плавление (кристаллизация): (4.13), где- удельная теплота плавления вещества,- масса расплавленного (затвердевшего) вещества;

3) испарение (конденсация): (4.14), где- удельная теплота парообразования вещества,- масса испарившегося вещества.

Еще одним следствием закона сохранения энергии является формула теплового баланса: в замкнутой системе общее количество отданного количества теплоты равно общему полученному количеству теплоты(4.15). Эта формула характеризует передачу энергии от одних частей изолированной системы к другим в процессе теплообмена.

Импульс тела (количество движения) – динамическая характеристика движения, связанная с силами, необходимыми для того, чтобы привести это тело в движение из состояния покоя или остановить его. По определению импульс тела– векторная физическая величина, равная произведению массы тела на его скорость:(4.16). Отсюда направление импульса всегда совпадает с направлением скорости движения тела, т.к. коэффициент-масса – положительное число.

Закон сохранения импульса можно формулировать двумя способами:

1. теоретически: в идеальных условиях (для замкнутых систем);

2. практически; для реальных условий (эти условия оговариваются).

Закон изменения импульса тела(прямое следствие второго закона Ньютона):(4.17) -изменение импульса тела равно импульсу действующей силы.

Величина называется импульсом силы. Таким образом,изменить импульс тела может лишь сила, действующая на него в течение некоторого промежутка времени.

В случае, когда правая часть (4.17) равна нулю, получаем форму закона сохранения импульса в векторном виде:или(4.18) - импульс тела в начальном и конечном состояниях (положениях) равны.

На основе формулы (4.17) выделяем случаи, в которых можно воспользоваться формулой (4.18):

1. внешние силы отсутствуют;

2. внешние силы есть, но они скомпенсированы;

3. внешние силы не скомпенсированы, но время их действия достаточно мало, т.е.(например, удар, сцепка вагонов, прыжок, выстрел, разрыв гранаты на осколки и т.д.);

4. если какой-либо из пунктов 1)-3) имеет место в отношении какой-то оси, например, оси х, то сохраняется лишь проекция импульса на эту ось: р_1х = р_2х (4.18*).

Методические указания. При решении задач на закон сохранения импульса надежнее следующее: там, где достаточно рассмотрения проекции импульса на некоторое направление, не стараться доказать выполнение и использовать закон сохранения импульса как вектора. Так как последний выполняется в случае изолированной системы (а таких систем в реальности нет, например, нельзя избавиться от силы тяжести для материальной частицы в пределах Земли) и в случае равенства нулю равнодействующей всех действующих на тело сил (НО… это условие должно выполняться в любой момент времени в процессе перехода тела из одного состояния в другое, а это иногда бывает вовсе не очевидно!). Короче говоря, при решении задач чаще всего необходимо руководствоваться пунктом 4) с формулой (4.18*). Хотя отдельный тип задач все же рассчитан на формулу для векторов - (4.18) (например, в случае разрыва гранаты на осколки имеем дело с трехмерным вектором).

Здесь же важно напомнить методическое требование: скорости (импульсы) всех тел или частей системы должны быть взяты относительно ОДНОЙ и ТОЙ ЖЕ ИСО для их включения в одно равенство!

Закон изменения и сохранения импульса можно обобщить и на случай системы тел (Замечание. Тела при этом рассматриваются как материальные точки!). Причем импульс системы может быть выражен через скорость ее центра масс.Центром масс(илицентром инерции) системы называется воображаемаяточкаС, положение которой зависит от распределения масс в системе и задается радиус-вектором по формуле:

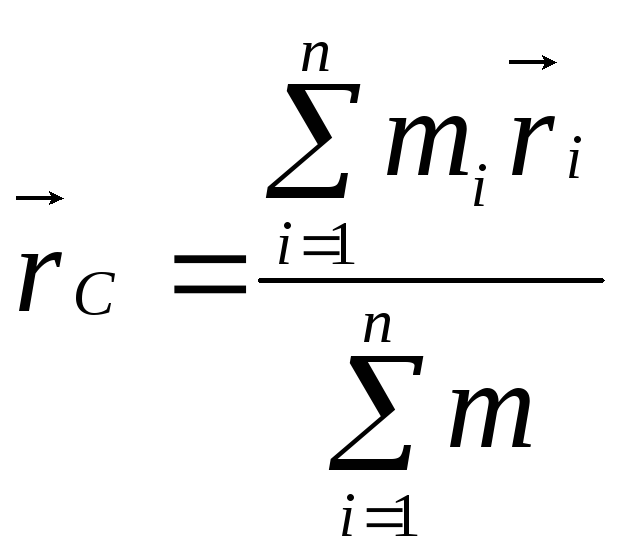(4.19), гдеn– число тел в системе,

m_i и- масса и радиус-векторi-того тела. Дифференцированием формулы (4.19) легко показать, что импульс системы равен произведению массы системы на скорость ее центра масс:(4.20).

Записав 2-й закон Ньютона для системы в форме:

получаем закон движения центра масс. Т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует равнодействующая всех внешних сил, приложенных к системе.

А в соответствии с законом сохранения импульса при выполнении одного из условий получим: центр масс системы либо движется равномерно, либо покоится.