Файл: Теория игр для экономистов doc.doc

при условии, что .

В чём смысл каждого из пяти критериев решение Нэша?

Первый. Рассмотрим игру с двумя участниками, полезности которых равны исоответственно (см. рис. 6.)

Рисунок 6

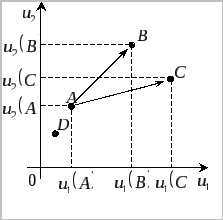
При переходе от A к B полезности обоих участников возрастают. Таким образом, B – Парето-эффективнее, чем A, и C – Парето-эффективнее, чем A. Сравнивая B и C, мы находим, что C – выгоднее, чем B для первого участника, но не выгодно для второго. Это обстоятельство говорит о том, что решения B и C являются несопоставимыми по Парето.

Если альтернативными для участников являются решения A, B и C, то рациональные участники отбросят решение A как Парето-неэффективное и оставят B и C. Очевидно, что оптимальным решением будет либо решение C, либо решение B.

Этот критерий означает, что игроки рассматривают только эффективные по Парето решения.

Второй. Этот критерий соответствует условиям индивидуальной рациональности.

Третий. Предположим, что общую сумму выигрышей двух участников увеличили вдвое. Очевидно, что вдвое увеличится полезность каждого из участников. Требуется ли при этом искать новые решения для этой комбинации? Если пользоваться решением Нэша, то этого делать не нужно. В частности, третий критерий означает, что переход от одной единицы измерения к другой не изменяет решения Нэша. Такие решения Нэша не изменятся, если каждой полезности добавить некоторую константу.

Четвёртый. Решение, найденное для одной нумерации, не изменится при другой нумерации.

Пятый. Если для случая, описанного на рис. 6, ввести четвёртую альтернативу D, то решение не изменится, потому что альтернатива D не будет рассматриваться отдельными игроками.

Решение Нэша называют также арбитражным решением. Это объясняется тем, что, если бы участники игры обратились к независимому арбитру для решения их торгового спора (т.е. для выбоора точки в переговорном множестве), то решение арбитра совпало бы с решением Нэша.

Пример. Пусть вожди племён (см. выше рассмотренный пример) обратились к старейшине (арбитру) для решения их спора. Требуется найти решение, которое примет старейшина.

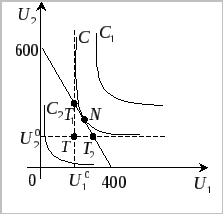
Решение. Найдём на плоскости множество Парето-оптимальных решений (см. рис.7). Для этого найдём функциональную зависимость между полезностями племёни. Ранее было получено, что на контрактной кривой имеет место система уравнений

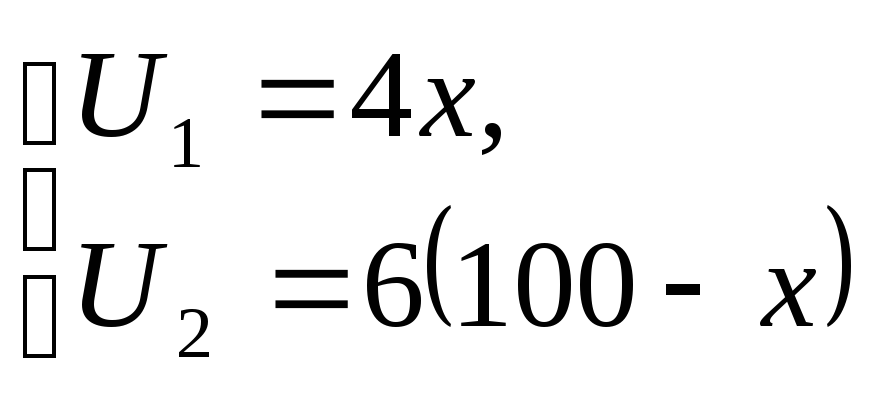
Рисунок 7

А

(3.10)

,

где .

Рассматривая кривую, на которой

гдеполучаем, что– уравнение гиперболы.

Максимизируя произведение (3.10), будем смещать гиперболу вверх и вправо до тех пор, пока она не окажется не границе допустимой области. В этом положении гипербола будет касаться кривой .

Уравнение (3.10) равносильно задаче об отыскании условного экстремума

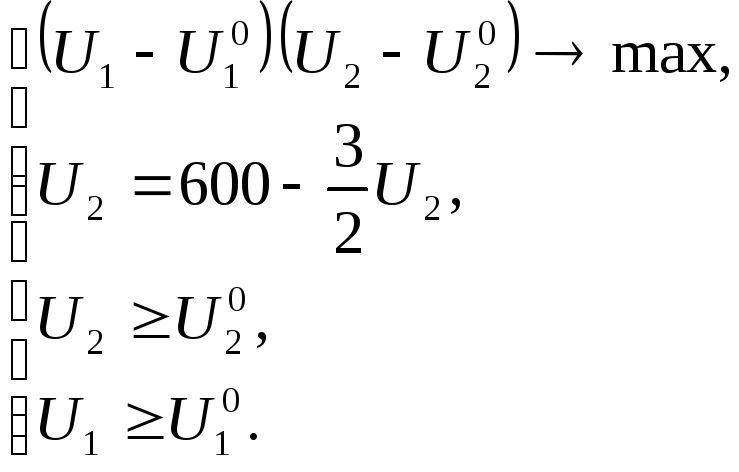
Решим эту задачу с помощью функции Лагранжа:

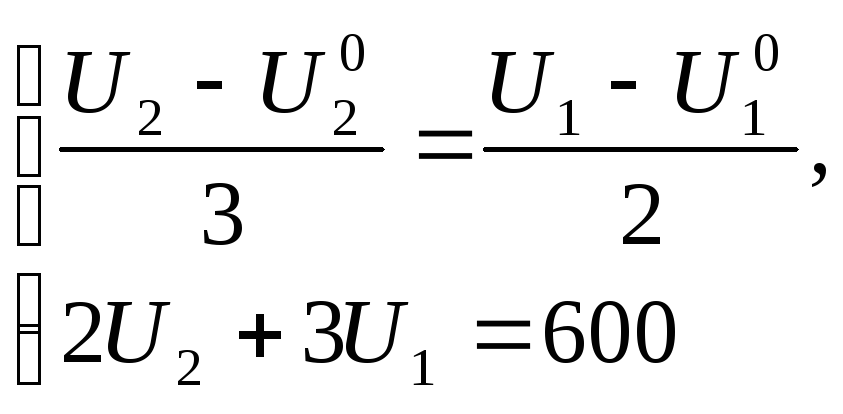
Решая эту систему, находим решение (единственное). Очевидно, что найденное решение ибудет координатами точки касания гиперболы и торгового множества.

Множество решенийкооперативной игры называется множеством Парето-оптимальных решений, если:

1. Для всех решений 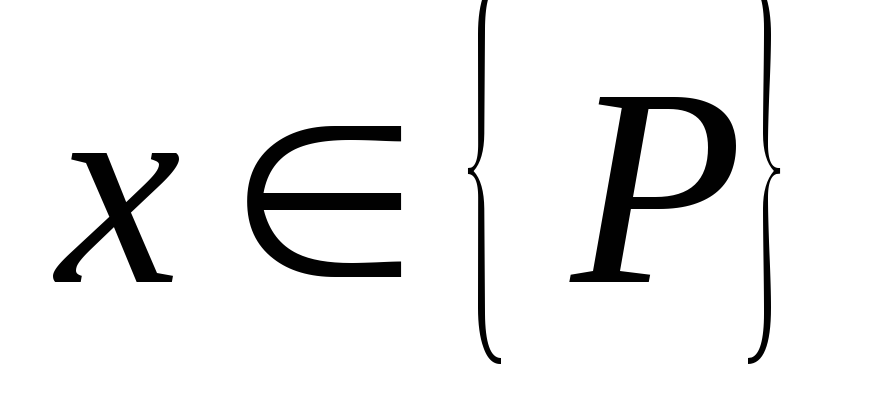найдётся такое решение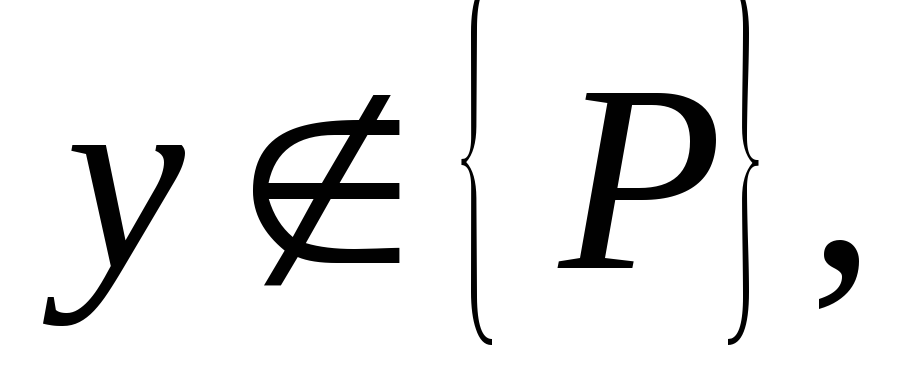что для первого участника решение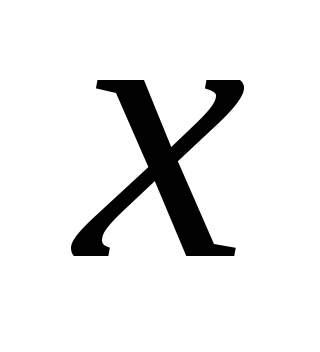будет лучше чеми не хуже чемдля всех остальных участников.

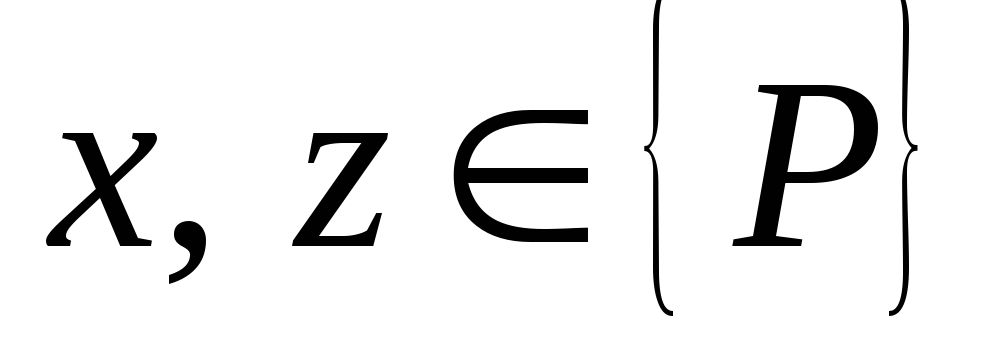2. Для всех двух решений переход от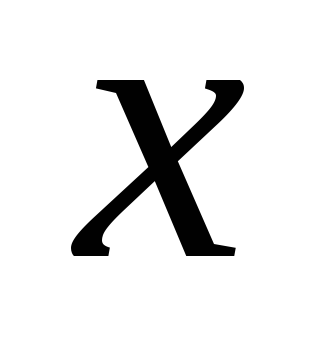к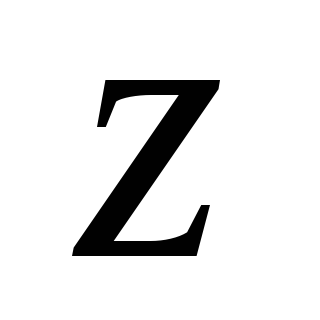улучшает положение хотя бы одного участника и ухудшает положение хотя бы одного другого. Т.е.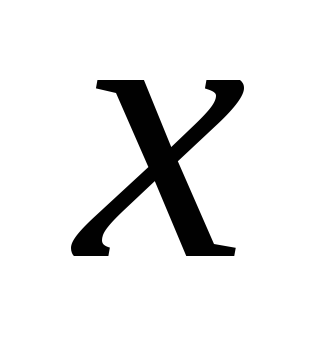иявляются решенияминесравнимыми по Парето.

На рис. 8. изображена область Парето-эффективных решений.

Рисунок 8

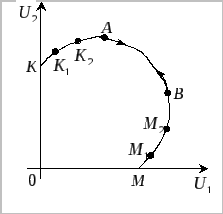
Все ли решения на кривой KM являются Парето-оптимальными? Т.к. ато получается, что область– область Парето-оптимальных решений. Дуга Парето-оптиальных решений всегда имеет отрицательный наклон. Вопрос о её выпуклости и вогнутости не имеет однозначного ответа.

Пример. Если два участника игры решают заключить контракт, т.е. решают предпринимать кооперативные действия, то их обмены будут располагаться на контрактной кривой. Пусть на контрактной кривой полезности участников связаны уравнением .

Решение. Найдём на плоскости множество Парето-оптимальных решений (см. рис.9).

Рисунок 9

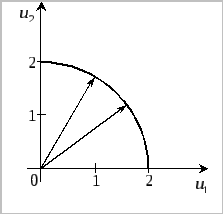
Пусть при прежних условиях

.

На рис.10 изобразим множество Парето-эффективых решений.

,

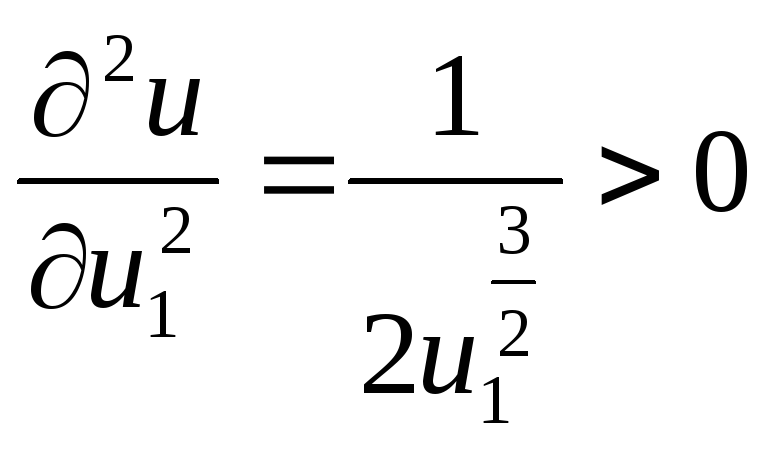т.е. кривая имеет отрицательный наклон и является вогнутой.

Рисунок 10

Для случая, когда в обмене участвуют товары, на которые распространяется закон Госсена (убывание предельной нормы замещения), характерна выпуклая форма Парето-оптимального множества. Эта форма используется в большинстве задач.

Практикум Матричная игра. Доминирование стратегий.

Задания для практических занятий.

№1. Игроки A и B записывают по две цифры: 1 или 2. Игра состоит в том, что, кроме своей цифры 1 или 2, каждый игрок записывает еще и ту цифру, которую, по его мнению, записал партнер. Если оба игрока угадали или оба ошиблись, то партия заканчивается вничью; если же угадал только один, то он получает столько очков, какова сумма записанных им цифр. Составить платежную матрицу игры.

Ответ:

№2. Армия полковника сражается с противником за контроль над позицией. Полковник имеет 2 полка, а противник – 3. Каждый из них может послать на позицию целое число полков. Позиция будет захвачена армией с большим числом полков. Составить платежную матрицу игры.

Ответ: