Файл: Теория игр для экономистов doc.doc

Если верхняя и нижняя цены игры принимают различные значения, то согласно теореме 1 справедливо строгое неравенство α<β. В этом случае применение первым игроком максиминной стратегии дает возможность второму игроку сделать свой проигрыш меньшим, чем число β, если он откажется от минимаксной стратегии. И наоборот, применение вторым игроком минимаксной стратегии дает возможность первому игроку сделать выигрыш большим, чем число α, если он откажется от максиминной стратегии. Тогда исход, который реализуется при максиминной и минимаксной стратегиях, не будет равновесным. Других равновесных исходов также не существует, следовательно игра без седловой точки не имеет решения в чистых стратегиях.

Пример. Найти решение игры.

			B
A	6	11	-5	2	8	-5
	17	-2	1	0	-15	-15
	-9	14	3	8	5	-9
	-1	-7	10	4	12	-7
	17	14	12	8	12

Решение.Чистой цены не существует. Равновесия в чистых стратегиях нет.

Пример. В платёжной матрице найти точку равновесия.

2 1	1	2	3	4	5	6	min
1	3	6	7	4	5	10	3
2	2	8	1	4	7	5	1
3	8	6	7		7	9	6
4	9	7	8	5	4	5	4
5	10	9	4	5	3	2	3
6	12	5	7	6	5	8	5
max	12	9	7	6	7	10

Точкой равновесия будет являться точка 6.

Пример. Посёлок Паново состоит из одной улицы. Два предпринимателя решили разместить свои киоски с продовольственными товарами. Других продовольственных магазинов в посёлке нет. Будем считать, что:

Оба киоска продают один и тот же ассортимент товаров по одним и тем же ценам;
Плотность жителей равномерно распределена по длине улицы.

Найти положение киосков, исходя из того, что каждый предприниматель стремится к наибольшей выручке.

Решение. Возьмём длину улицы за 1, тогда весь посёлок расположится на отрезке (Рис.1)

Рисунок 1

Обозначим x – координата первого киоска; y – координата второго киоска. Очевидно, что

Найдём выручку X первого киоска. Цену товара возьмём за 1.

–середина расстояния между x и y.

Первый предприниматель решает задачу ,

а второй соответственно .

Таким образом, получаем игру с постоянной суммой, равной 1.

Применим принцип гарантированного результата. Первый предприниматель ожидает, что второй будет выбирать такое значение y, чтобы выручка первого была минимальной, то есть он исходит из пессимистических ожиданий:

1-й выбирает такой x, чтобы :

2-й выбирает такой y, чтобы:

Найдём оптимальные стратегии:

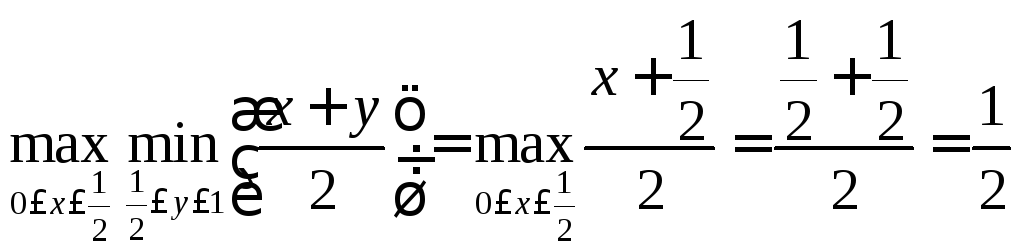
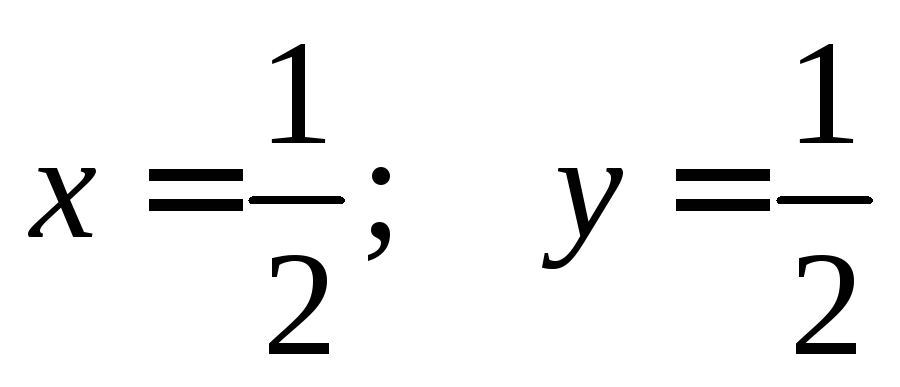
Аналогично

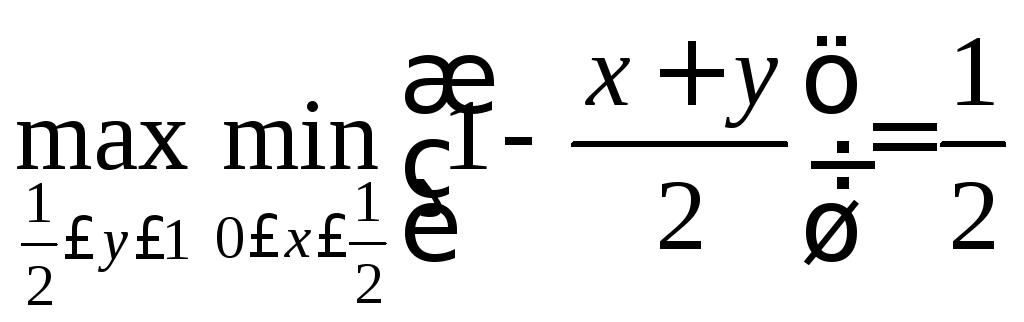
Таким образом, лучшими стратегиями будет размещение киосков на середине улицы спиной друг к другу. Это равновесие не выгодно жителям посёлка, но обеспечивает равновесие между предпринимателями.

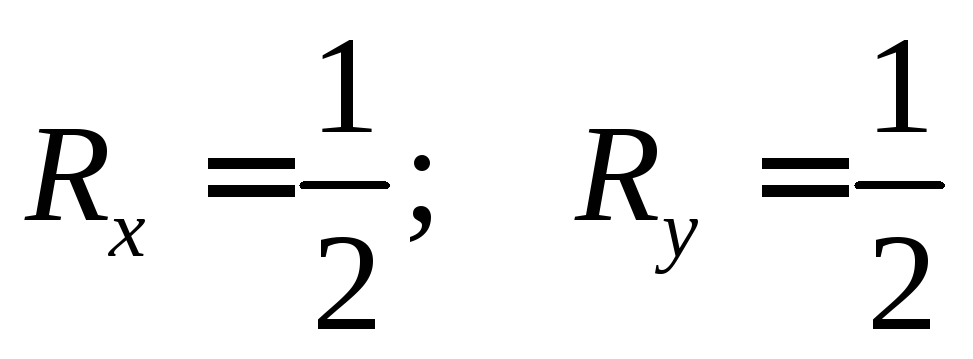
В примере два конкурента фактически борются за долю, превышающую, т.е. за выигрыш

где – функция платежа,

если – выигрышx – выигрышy.

Равновесие: .

§2.1.4. Смешанное расширение игры

Пусть матричная игра представлена платежной матрицей с элементами a_ij, где i=1,2,…,m – стратегии первого игрока, j=1,2,…,n – стратегии второго игрока. Данные стратегии игроков будем называть чистыми стратегиями.

В предыдущем параграфе мы доказали, что решение матричной игры в чистых стратегиях (т.е. при выборе каждым игроком одной и только одной стратегии из заданного множества его стратегий) существует тогда и только тогда, когда платежная матрица имеет седловую точку. Рассмотрим выбор стратегий в игре без седловой точки. Если игрок может предвидеть, какую из чистых стратегий изберёт противник, он может найти наилучший ответ на ход противника. Таким образом, каждый игрок заинтересован в том, чтобы его ходы были непредсказуемы. Для этого необходимо ввести в выбор стратегий элемент случайности. Однако отсутствие логики при выборе стратегий ухудшит положение каждого из игроков. Компромисс заключается в том, что игроки чередуют (смешивают) свои стратегии случайным образом, но по определённой разумной схеме. Этой схеме должна соответствовать комбинация чистых стратегий.

Введем следующие изменения правил игры: каждый игрок наряду с отдельными стратегиями из своего множества стратегий может применять их комбинации, в которых стратегии представлены в определенных пропорциях.

Рассмотрим матричную игру, представленную Таблицей 5.

Таблица 5

2-й игрок