Файл: Оценка без отметки Цукерман.docx

Вынести решение о том, сколько баллов следует начислять за каждое задание, не всегда возможно заранее, до выполнения зада­ния. Чаще это решение класс принимает только после того, как за­дание выполнено и обсуждено. Особенно характерно это для задач, имеющих несколько верных решений. К примеру, на доске записаны две схемы

Ученикам предлагается составить к этим схемам уравнения, «кто сколько успеет». Сначала каждый ребенок работает самостоятель­но. Учитель, заглядывая в тетрадки, приглашает к доске детей, со­ставивших уравнения нового типа (не важно, правильны они или нет). Когда на доске записаны все разные варианты уравнений, кото­рые придуманы в классе, учитель просит автора каждого уравнения защитить его: доказать, что оно подходит к схеме. После аргументи­рованного спора правильные уравнения остаются на доске, непра­вильные стираются. Подсчитывается, сколько уравнений в принци­пе можно было бы составить к каждой схеме. За каждое верное урав­нение начисляется один балл. Только теперь дети могут сами назна­чить «цену» каждого задания: 8 уравнений можно было составить к первой схеме, 9 — ко второй.^* Всего за работу можно было полу­чить 17 баллов. Когда определен высший уровень достижений, дети подсчитывают свои результаты и переживают свой успех или не ус­пех в зависимости от собственного уровня притязаний. Для одного ребенка оценка «15 баллов из 17 возможных» — это поражение: он стремится к абсолютному первенству. Для другого та же оценка — это огромный успех: только два ученика в классе смогли сделать лучше!

Конечно, не в каждом классе дети даже сообща составят все 17 возможных уравнений. Возможны две тактики действий учителя — более и менее жесткая. Более жесткая тактика: показать детям выс­ший уровень достижений, не достигнутый не только отдельными учениками, но и всем классом. Когда класс исчерпал свой запас урав­нений, учитель может сам добавить те уравнения, до которых класс сегодня не додумался. И ни один ребенок не получит высший балл. Если класс находится в отличной рабочей форме, эта тактика «об­щего проигрыша» может принести свои мотивационные плоды: на­завтра кто-то из честолюбивых детей постарается добиться высше­го результата. Если класс утомлен, если тонус класса снижен, стоит прибегнуть к более мягкой тактике оценивания: исходить из того числа уравнений, которые были сегодня составлены в классе, не повышать уровня требований раньше, чем дети будут готовы взять более высоко поставленную планку.

Две разных оценочных тактики возможны по отношению к оши­бочным решениям. Можно вычитать очки за каждое «лишнее» урав­нение. Это отучит детей, погнавшихся за баллами, от бессмыслен­ной манипуляции данными задачи в расчете на то, что какое-нибудь из наугад составленных уравнений может оказаться правильным. Другая тактика адресована детям, которые боятся рисковать и пред­почитают вообще ничего не делать, лишь бы не потерпеть неудачу. Такие ученики, если их наказывать за ошибки (вычитать баллы за неверные уравнения), предпочтут пораженческие методы работы: будут делать лишь тот минимум, за который могут ручаться, и не рискнуть высказать (записать) мысль, которая лишь кажется верной, но не обладает 150% запасом прочности. В классе есть и ученики, склонные избегать неудач, и ученики, стремящиеся к победе любой ценой (даже с помощью гаданий и бездумных манипуляций цифра­ми и буквами). Поэтому ни одна оценочная стратегия не является универсальной, обе имеют право на существование, и стоит приме­нять то один, то другой метод реагирования на ошибки.

Приведем пример балльной оценки контрольной работы по ма­тематике в 1 классе. Контрольная работа состояла из пяти заданий по теме «Уравнение».

В первом задании учитель читает тексты задач (их четыре), а дети составляют к ним уравнения. Например, «В гараже стояло 15 машин. Когда несколько машин уехало, то осталось девять. Сколько машин уехало?». Дети должны составить уравнение: 15 — X = 9.

За каждое верное уравнение ученику начисляется один балл, таким образом, за первое задание можно получить от нуля до четы­рех баллов.

Во втором задании детям предлагалось составить программу для того, чтобы найти неизвестное по данному чертежу. Чертежа было два:

Соответственно, детям предстояло составить две программы: Х = Е + Т и Х = В — А.

За каждую правильную программу начислялся один балл, та­ким образом, за верно выполненное второе задание ученик получал два балла, а если верна была лишь одна из программ — один балл.

В третьем задании по готовому чертежу надо было составить уравнения (кто сколько сможет). Верных уравнений могло быть че­тыре:

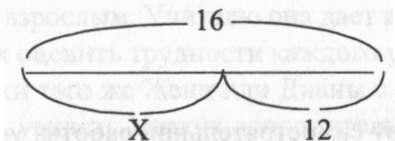
16 — X = 12

16— 12 = X

12 + Х= 16

Х+ 12 = 16

Каждое верное уравнение оценивалось одним баллом, таким образом, максимальное количество баллов за третье задание равно четырем.

Иногда дети составляли неверные уравнения (например, 16 + 12 = X или X — 12 = 16), и тогда общее число уравнений в работе ученика могло быть больше четырех. Каждое неверное урав­нение «забирало» один балл.

К примеру, ученик записал три уравнения: первые два верные, последнее — неверное: 16—12 = X; 16 — X = 12; X—12=16. Этот ученик за третье задание получает одни балл (2 — 1).

В четвертом задании были даны четыре уравнения, которые надо было решить с помощью чертежей. Одно из уравнений было специально составлено неверно; ученики должны были обозначить его знаком «ловушки» и не составлять к нему чертеж. Каждое верно составленное уравнение оценивалось в один балл. Умение узнать «ловушку» тоже оценивалось баллом. Итого, за четвертое задание ученик мог получить от нуля до четырех баллов.

Пятое задание было самым трудным, так как предполагает рефлексию всех тех способов действия, которые использовались для выполнения предыдущих заданий. К готовому решению (X = А — В) надо было составить чертеж и уравнения.

Так как это задание было самым трудным, оно «стоило» пять баллов. (Вопрос о сравнительной трудности заданий специально обсуждался с классом при анализе результатов работы.) Тот, кто со­ставил верный чертеж, но не смог составить уравнения, получал два балла. У кого чертеж был неверным, не получал ни одного балла.

Таким образом, максимальное количество баллов, которое уче­ник мог получить за эту контрольную работу, — 19:

1. задание — 4 балла,

2. задание — 2 балла,

3. задание — 4 балла,

4. задание — 4 балла,

5. задание — 5 баллов.

На уроке, посвященном анализу самостоятельной работы, учи­тель раздает детям их контрольные тетради и подробно объясняет, сколько баллов начисляется за каждое задание (дети сами посчита­ют количество плюсиков, стоящих рядом с каждым правильным чер­тежом или уравнением) и как складывается суммарный балл.

После того, как дети получат несколько опытов балльной оцен­ки своих работ и привыкнут к тому, что суммарное количество бал­лов за работу всегда разное (такая система балльной оценки прин­ципиально отличается от пяти, десяти, сто балльной системы), с ними стоит в открытую обсуждать, как именно начисляются баллы. По­сле очередной контрольной работы по математике учитель спраши­вает класс, какое задание было самым легким и самым трудным и почему. За самое легкое задание начисляется один балл, за задание средней трудности — два балла, за трудное задание — три балла. Так, крупица за крупицей, у детей складывается важнейшая способ­ность к объективной оценке и самооценке. Однако следует помнить, что эмоциональная сторона оценки не входит в такую объективную оценку; похвала взрослого и одноклассников за идеально выполнен­ную работу совершенно необходима маленькому ребенку, даже если он виртуозно овладеет критериями объективного оценивания.

Как учитель оформляет балльную оценку? Кроме «плюсиков» и суммарного балла на полях ученических тетрадей, учитель, как пра­вило, заносит результаты самостоятельной работы в таблицу. При­ведем две строки этой таблицы, демонстрирующие высший и низ­ший уровень достижений в описанной выше работе.

Нет нужды объяснять, почему такая таблица может быть полез­на взрослым. Учителю она дает возможность объективно, не на гла­зок оценить трудности каждого ученика, сравнить сегодняшние ус­пехи того же Жени или Дианы с их прежними и будущими успеха­ми, увидеть, в каких дополнительных упражнениях нуждается класс в целом и отдельные ученики.

Неоценима такая форма представления результатов детских са­мостоятельных работ и для бесед с родителями. Когда ребенку не ставят отметок, родителям подчас бывает нелегко самостоятельно оценивать уровень достижений своих детей. Некоторые родители впадают в чрезмерное благодушие, некоторые, напротив, испыты­вают постоянную, ничем не обоснованную тревогу, заражая ею сво­их детей. Так, к учителю математики в апреле пришла робкая и обес­покоенная мама первоклассника с просьбой дать Косте дополнитель­ные задания. Учительница удивилась и отказалась дополнительно нагружать ребенка, который работает на уроках с полной отдачей и чрезвычайно успешен. Она дала ряд советов Костиной маме о том, как организовать полноценный отдых ребенка после трудового дня, но настоятельно просила не заниматься с ребенком дополнительно, особенно весной, когда у большинства городских детей отмечаются признаки астении.

Мама Кости была удивлена, она пожаловалась на то, что дома Костя не всегда может подробно объяснить то, что он делал на уро­ке и прокомментировать свои собственные записи в тетрадке по ма­тематике. «Не следует ли из этого, что Костя не все усваивает, что ему необходимо помочь?» — спросила мама. Ответить беспокой­ной маме помогли таблицы. Учительница показала, что практиче­ски все самостоятельные работы по математике, даже самые слож­ные, с которыми справлялось лишь несколько человек в классе, Костя делал без ошибок. После этого несколько успокоенная и приятно взволнованная мама была готова выслушать разъяснения учитель­ницы о возрастных нормах речевого развития младших школьни­ков, о том, что даже весьма развитый и способный ребенок семи- восьми лет не всегда в состоянии восстановить логику урока. «Пред­ставьте себе, что Вы — участник постоянно действующего научно­го семинара. Дискуссии в этом многолюдном семинаре длятся уже не первый месяц. Посторонний человек просит Вас рассказать, что было на семинаре сегодня. Задача выполнимая, но очень непростая: Вам надо обрисовать и общий предмет обсуждения, и те промежу­точные результаты, к которым участники пришли за месяцы общей работы, и мнения отдельных выступающих... Едва ли можно пред­полагать, что маленький мальчик сумеет сделать такой доклад, а именно это Вы и просите, когда спрашиваете: «Что было сегодня на уроке?» Давайте пока обе радоваться тому, как успешно Костя ра­ботает на уроке. Вы сами видите, что он справляется самостоятель­но с самыми сложными заданиями. У меня сейчас только одно бес­покойство: на первых уроках Костя очень вял. Достаточно ли он спит? гуляет? получает витаминов?» — так учительница может пе­реключить внимание тревожной мамы в достойное русло заботы о здоровье ребенка. Этому в высшей степени способствуют таблицы, показывающие, с одной стороны, успехи мальчика, с другой сторо­ны, его рейтинг в классе. (Говоря о том, что по математике Костя стоит в классе в первой десятке, учительница прикрывает левую графу таблицы со списком класса, показывая Костиной маме только графу результатов. Таким образом, разговор о Косте не может по­вредить другим ученикам.)

Нужны ли подобные таблицы для самого главного этапа оценки самостоятельных работ, когда результаты работы представляются детям? Первоклассникам важна лишь последняя графа таблицы: «Итоги». При анализе контрольной работы учитель объясняет де­тям, каким образом подсчитываются баллы, а далее сообщает, кто сколько баллов набрал. Объяснить результат работы Жене Ш. и дру­гим первоклассникам, набравшим высший балл, очень легко: «Вы молодцы, все сделали правильно. Лучше эту работу выполнить было невозможно!» Для маленького ребенка такая похвала практически равнозначна «пятерке» как знаку высших школьных добродетелей. Правда, в оценке «19 баллов из 19 возможных» по счастью не содер­жатся все те личностные оттенки, которые заложены в оценке «от­личник»: ученик, получивший 19 баллов, это тот, кто лучше других решил уравнения, а не самый лучший человек в классе.