Файл: Теория игр для экономистов doc.doc

Имеет ли первая фирма возможность добиться выигрыш 100 с помощью стратегического хода?

Решение.

Для решения следует ответить на следующие вопросы:

1. Имеет ли вторая фирма доминирующие стратегии?

Вторая фирма имеет одну доминирующую стратегию – низкая цена.

2. Что является следствием из этого?

Какие бы действия не предпринимала первая фирма, вторая фирма будет назначать низкую цену.

3. Какая из фирм доминирует на рынке?

Доминирующей на рынке является первая фирма, т.к. её продукция является более разнообразной.

4. Как будут восприняты второй фирмой действия первой, которые она может предпринять для того, чтобы убедить вторую фирму назначить высокие цену?

Как пустые угрозы.

5. Почему второй фирме не стоит воспринимать угрозы первой всерьёз?

Что бы ни делала первая фирма, вторая фирма знает, что первой фирме, при снижении цены на свою продукцию, будет только хуже.

6. Что изменится, если вторая фирма знает, что у первой фирмы репутация рискованного иррационального игрока?

В этом случае вторая фирма может поверить угрозам первой фирмы.

В данном случае реализации наиболее выгодного для первой фирмы равновесия по Штакельбергу мешает наличие доминирующих стратегий у второй фирмы.

Пустые угрозы могут быть также следствием равновесия по подыграм (Sub games Equilibrium), что демонстрирует пример «Заложник – террорист»

Пример: Пустые угрозы в игре “заложник-террорист”. Информированные агенты.

Террорист захватил заложника и требует от него выкуп, условный размер которого возьмем за 1. Террорист угрожает взорвать заложника вместе с собой, если выкуп не будет выплачен. Оба участника знают потери друг друга при неблагоприятном исходе игры, т.е. при взрыве. Какое решение должен принять заложник?

Решение. Изобразим дерево решений (рис. 3), и разобьем игру на подыгры.

Рисунок 3

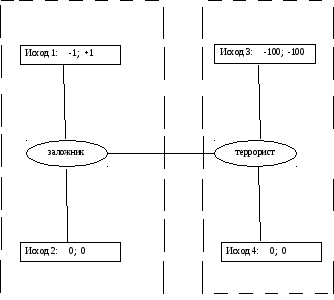
Subgame2 Subgame1

1 платить выкуп 3 взрывать

2 не платить выкуп 4 не взрывать

В подыгре 1 (Subgame1) террорист имеет доминирующую стратегию «не взрывать».

В подыгре 2 (Subgame2) заложник имеет доминирующую стратегию «не платить».

Глава 3. Кооперативные решения

§3. 1. Понятие коалиционной игры

В экономике отдельные субъекты редко действуют поодиночке. Чаще всего они объединяются в союзы, коллективы, кооперации для достижения своих целей. Интуиция и практика показывают, что коллективные действия могут существенно увеличивать эффективность их участников. Коллективные действия можно разделить на три ступени взаимодействия:

а) обмен информацией;

б) совместный выбор стратегий участников (договор о совместных действиях);

в) объединение ресурсов и последующий выбор совместных действий на основе объединенных ресурсов.

Математические модели конфликтов, участники которых могут предпринимать коллективные действия, изучаются в теории коалиционных игр. Коалиционной игрой называется игра с непротивоположными интересами, в которой игроки могут обсуждать перед игрой свои стратегии, договариваться о совместных действиях,заключать союзы (коалиции)для объединения ресурсов.

Коалиция представляет собой добровольное объединение участников игры, согласившихся осуществлять совместные действия (совместные стратегии). Объединение игроков в коалицию означает их сотрудничество, согласие по поводу выбора общего, т.е. кооперативного решения. Общее решение всех участников коалиции определяет стратегию коалиции. Возможны случаи, когда участники игры объединяются в коалицию только для осуществления коалиционной стратегии, а после этого коалиция распадается.

С математической точки зрения, коалиция представляет собой некоторое подмножество участников игры. Обозначим I={i} (i=1,2,…n) множество игроков, произвольную коалицию будем обозначать K. Общее число всех возможных коалиций, т.е. всех подмножеств множества I, включая пустое подмножество, равно , где– число сочетанийm по n. Число сочетаний является количеством всех всевозможных коалиций на множестве из n игроков, в каждую из которых входятm участников.

Формальное описание полностью определенной коалиционной игры можно задать с помощью следующих параметров:

1. Множество участников .

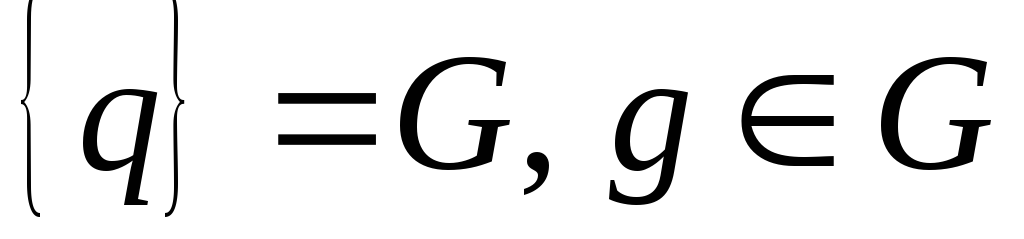2. Множество всех коалиций K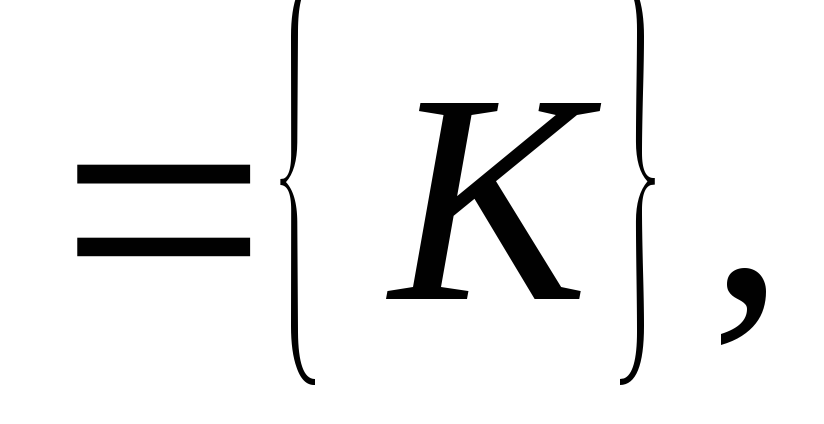где отдельная коалиция 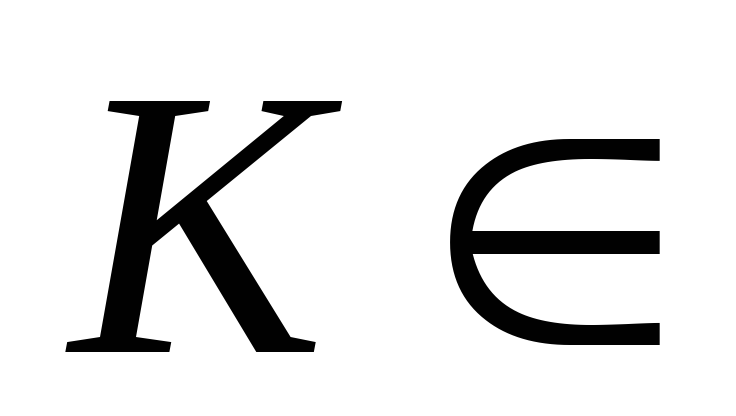K является подмножеством множества 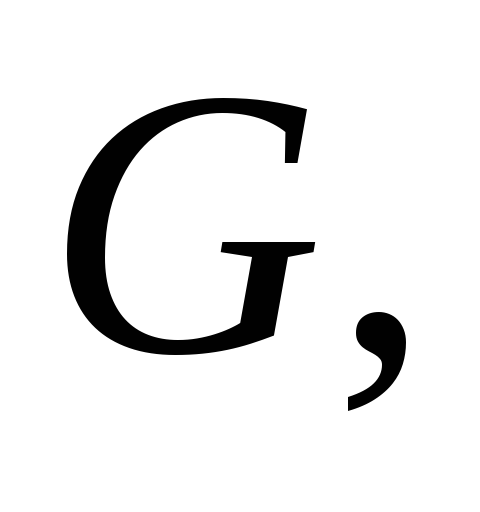т.е., включая пустое множество игроков.

K – коалиционное разбиение множества игроков.

3. Для каждой коалиции 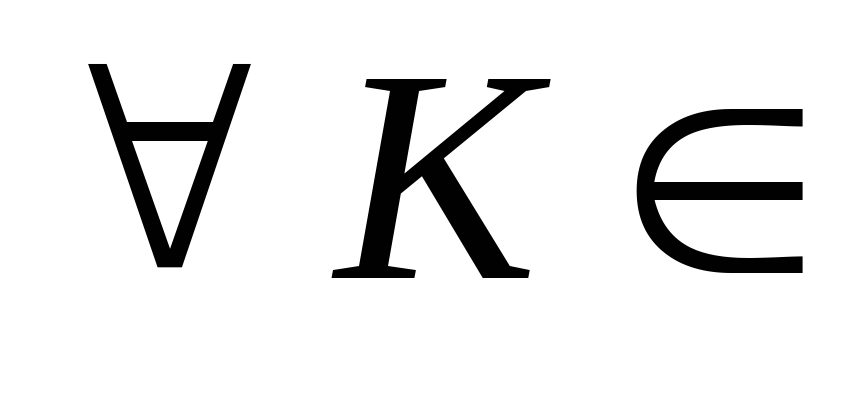K должно быть определено множество (набор) стратегий X_K={x_K}

4. Множество исходов игры S=∏X_K, где исход s€S определяется выбором коалициями своих стратегий x_K.

5. Для каждого исхода игры s€S и каждой коалиции 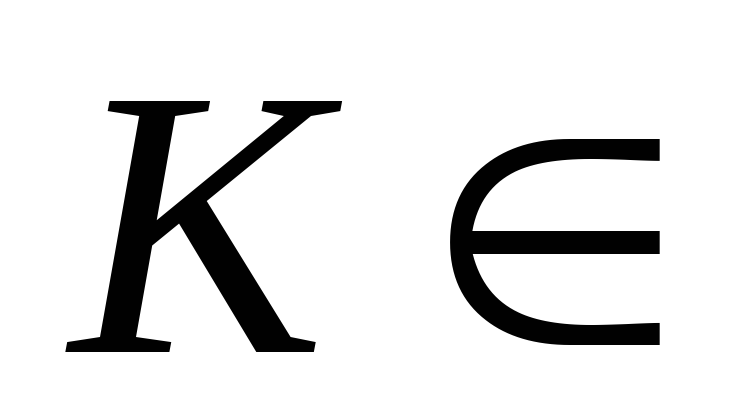K определён общий выигрыш коалиции H_K(s).

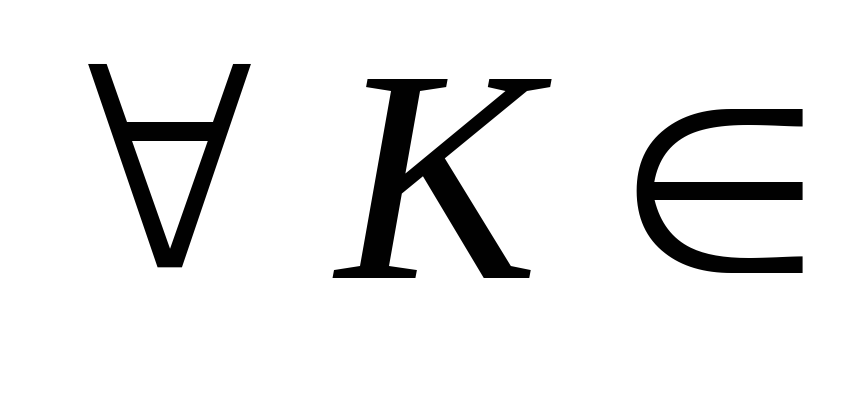6. K определена схема дележа выигрыша коалиции H_K(s) между участниками коалиции при каждом исходе x

H_K(s)=∑h_i(s)

где h_i(s) – выигрыш игрока i из коалиции K.

Исход коалиционной игры при заданных стратегических возможностях всех игроков определяется, во-первых, разбиением множества игроков на коалиции, (т.е. коалиционным разбиением K множества I), во-вторых, множествами возможных стратегий каждой из коалиций, в-третьих, стратегиями, которые коалиции выбирают из своих наборов стратегий.

Игровые возможности каждой отдельной коалиции K могут быть определены с помощью ее характеристической функции v_K, равной гарантированному математическому ожиданию выигрыша данной коалиции при применении смешанной стратегии, составленной из стратегий X_K={x_K}.

Смысл характеристической функции поясним на следующем примере.

Пример «Война за ресурс»

Три королевства борются за владение нефтяным месторождением. Если они договорятся о долевой эксплуатации, то их суммарный доход составит 111 единиц. Если два королевства объединятся для войны против третьего, то с учетом издержек на ведение войны суммарный доход уменьшится. Пусть каждая из двух образовавшихся коалиций имеет две стратегии – оборонительную и наступательную. Для коалиционного разбиения {1-е и 2-е} против {3-го} доходы сторон в зависимости от исходов игры приведены в таблице 1. Для коалиционного разбиения {1-е и 3-е} против {2-го} доходы сторон в зависимости от исходов игры приведены в таблице 2. Для коалиционного разбиения {2-е и 3-е} против {1-го} доходы сторон в зависимости от исходов игры приведены в таблице 3. Если каждое королевство будет воевать против двух других, то в результате 1-е получит доход 30 единиц, 2-е и 3-е получат по 15 единиц. Найдем характеристические функции каждой из коалиций.

Таблица 1

Таблица 2

Таблица 3

Решение.

Рассмотрим игру, заданную таблицей 1. Легко обнаружить, что в игре нет равновесий по Нэшу в чистых стратегиях и найти равновесные смешанные стратегии каждого их игроков x^*= {1/2;1/2}, y^*= {1/2;1/2}. При этих стратегиях все исходы равновозможны, следовательно, гарантированное ожидание выигрыша коалиции {1-е и 2-е}, т.е. характеристическая функция v{1-е и 2-е}=(90+50+50+90)/4=70. Характеристическая функция коалиции, состоящей из одного игрока (3-е королевство) v{3-е} =(10+50+50+10)/4=30.

Аналогично, из таблицы 2 находим характеристические функции

v{1-е и 3-е}=(80+50+50+80)/4=65, v{2-е} =(20+50+50+20)/4=35.

Из таблицы 3 находим характеристические функции

v{2-е и 3-е}=(60+50+50+60)/4=55, v{1-е} =(40+50+50+40)/4=45.

Война всех против всех будет невыгодна каждой из рассмотренных коалиций, т.к. в ней соответствующие характеристические функции принимают меньшие значения. Наконец, при договоре о долевой эксплуатации месторождения, коалиционное разбиение имеет вид