Файл: Теория игр для экономистов doc.doc

Р. Аксельрод дал ответ на этот вопрос, предложив в повторяющейся игре стратегию «Зуб за зуб». Рассмотрим эту стратегию на примере «Дилемма заключенных» (таблица 333), предполагая, что данная ситуация разыгрывается бесконечное число раз.

Таблица 11

Обозначим t=0,1,2… очередной шаг игры, H_it – выигрыш игрока i (i=1,2) на шаге t, H_it принимает значения из таблицы 333 в зависимости от стратегий игроков на шаге t. Эти стратегии будем обозначать S_it (i=1,2). Выигрыш каждого игрока i (обозначим H_i) будет складываться из его выигрышей на всех шагах игры H_it, однако, с учетом дисконтирования (снижения цены) выигрыша на каждом последующем шаге. Дисконтированные суммы часто применяются в экономических расчетах и основаны на соображении, что будущие прибыли значат для их получателя меньше, чем прибыли в настоящий момент, то же касается и убытков. Потому будем считать, что выигрыш игрока i на шаге t будет им оцениваться в момент (t-1), как величина d·H_it, где 0<d<1. Величина d называется коэффициентом дисконтирования. Дисконтированная сумма выигрыша игрока i от всей игры будет определяться по формуле

H_i= H_i0+ d·H_i1+ d²·H_i2 +…+ d^t·H_it+… (2.13)

Стратегия «Зуб за зуб» состоит в следующем выборе стратегий S_it (i=1,2) на каждом шаге t:

Если на шаге (t-1) хотя бы один из игроков применил стратегию «сознаваться», то стратегия S_it будет «сознаваться»;

Если на шаге (t-1) оба игрока применили стратегию «не сознаваться», то стратегия S_it будет «не сознаваться».

Очевидно, что результат всей игры будет зависеть от стратегий, выбранных игроками на начальном шаге t=0.

Если S_1,0= «сознаваться» и S_2,0= «сознаваться», то все последующие стратегии будут «сознаваться», тогда

H₁= H₂= -4 - d·4 - d²·4-…- d^t·4-…=-4/(1- d), (2.14)

по формуле суммы геометрической прогрессии.

Если S_1,0= «не сознаваться» и S_2,0= «не сознаваться», то все последующие стратегии будут «не сознаваться», тогда

H₁= H₂= -2 - d·2 - d²·2-…- d^t·2-…=-2/(1- d). (2.15)

Если S_1,0= «сознаваться» а S_2,0= «не сознаваться», то все последующие стратегии будут «сознаваться», тогда

H₁= -1 - d·4 - d²·4-…- d^t·4-…=-1-4d /(1- d), H₂=-7-4d /(1- d). (2.16)

Если S_1,0= «не сознаваться» а S_2,0= «сознаваться», то все последующие стратегии будут «сознаваться», тогда

H₂= -1 - d·4 - d²·4-…- d^t·4-…=-1-4d /(1- d), H₁=-7-4d /(1- d). (2.17)

Таким образом, в зависимости от начальных стратегий игроков возможны 4 исхода, представленные в таблице 12.

Таблица 12

Исход (-2/(1- d);-2/(1- d)) является оптимальным по Парето, этот исход будет равновесным по Нэшу тогда и только тогда, когда справедливо неравенство -2/(1- d)≥-1 -4d/(1- d), что верно при d≥1/3.

Итак, при достаточно большом коэффициенте дисконтирования стратегия «Зуб за зуб» делает наиболее благоприятный для всех игроков исход равновесным по Нэшу: если один заключенный не сознается, то другому также выгодно не сознаваться.

Применительно к примеру «Назначение цены» стратегия «Зуб за зуб» имеет следующий смысл. Если игра «Назначение цены» разыгрывается бесконечное число раз, то один из предпринимателей начинает с высокой цены и удерживает её до тех пор, пока второй предприниматель тоже придерживается высокой цены. Если второй назначит низкую цену, то первый тоже понизит свою цену. На практике существует возможность, что если второй предприниматель осознает свою ошибку и вернётся к высокой цене, то первый поступит также.

Стратегия «Зуб за зуб» позволяет достигать эффективного по Парето исхода, если игра повторяется бесконечное число раз. В реальности ни один процесс в экономике не длится бесконечно долго, поэтому предположение о бесконечном числе разыгрывания не реалистично.

Предположим, что игра «Назначение цены» разыгрывается конечное число раз, например 5 лет (60 месяцев). Как изменится рациональные соображения участников при конечном числе разыгрывания? Каждый участник игры выбирает стратегию «Зуб за зуб», потому что, отклонившись от неё в n-м периоде, он будет наказан впериоде. Однако в данном случае 60-й период является последним. Воспроизведём логику рассуждений первого участника игры: «Если я буду сохранять высокую цену 59 периодов, а в 60-м назначу низкую цену, то я получу дополнительный выигрыш, а другие участники не успеют меня наказать за отклонение от общей стратегии». Далее первый участник может предполагать, что другие игроки рассуждают аналогично, следовательно, есть смысл первому нарушить негласный договор. Тогда первый участник склонен отклониться от общей стратегии уже в 59-м, а не в 60-м периоде, и т.д. Таким образом, стратегия«Зуб за зуб» теряет устойчивость на протяжении всего разыгрывания.

Существуют, однако, предпосылки для того, чтобы стратегия «Зуб за зуб» применялась на олигополистическом рынке. Предположим, что фирма 1 имеет хотя бы небольшие сомнения в том, что ее конкурент абсолютно рационален, т.е. в том, что он просчитал всю логическую цепочку. Тогда фирма 1 будет сомневаться, в том, что конкурент назначит низкую цену в последнем периоде, тогда фирме 1 нет смысла отказываться от высокой цены в предпоследнем периоде и т.д. Имеются практические примеры, как устойчивости, так и неустойчивости стратегии «Зуб за зуб».

Пример относительной устойчивости: «Рынок водомерных счётчиков»⁴

Производителями на рынке водомеров в США на протяжении более чем 30 лет были 4 фирмы, одна из которых имела долю на рынке примерно в 35%, остальные три вместе – от 50 до 55%. Особенность рынка водомеров в том, что спрос (его представляли коммунальные службы муниципалитетов) был неэластичен и стабилен. Так же стабильными были издержки производителей. Продукция однотипная, так что рынок водомеров можно рассматривать как пример однородной олигополии. При таких условиях четыре фирмы могли бы получать высокую монопольную прибыль. Общая ценовая стратегия фирм – назначение высокой цены – наблюдалась в течение шести лет. Прямой сговор не мог реализоваться в силу действия антимонопольного закона, но фирмы могли довольно долго следовать стратегии «Зуб за зуб».

Пример неудачи при выработке общей ценовой стратегии: «Рынок авиаперевозок»⁵.

В 1983 году президент компании «American Airlines» предложил другим авиакомпаниям использовать единую схему образования тарифов в зависимости только от расстояния между аэропортами. Цель состояла в ограничении ценовой конкуренции и достижении неявного сговора в ценообразовании. Большая часть авиакомпаний отнеслась доброжелательно к предложенному плану. Однако, в итоге план был сорван, т.к. компания «Pan Am», недовольная своей долей рынка начала снижать цены, вводя различные скидки, и вскоре ей последовали другие компании. Разыгралась «Дилемма заключенных, или, как выразился один из экономистов, сговор был нарушен зубилом конкуренции.

При ограниченном количестве розыгрышей стратегия «Зуб за зуб» теряет устойчивость. Всё же в отдельных случаях она может оказаться эффективной. Предпосылки стратегии «Зуб за зуб»:

1. Малое число компаний и удовлетворённость каждой из них совей долей рынка;

2. Стабильный спрос и издержки;

3. Участники игры сомневаются в том, их конкуренты способны всё рационально подсчитать. Например, первый участник, сомневаясь в том, что второй участник абсолютно рационален, думает: «Может быть, он не сообразит снижать цену в 60-м периоде, тогда мне выгоднее придерживаться стратегии «Зуб за зуб» на протяжении 59 периодов».

§2.2.6. Последовательные игры

До сих пор мы предполагали, что участники игры делают свои ходы одновременно, т.е. одновременно выбирают свои стратегии. Однако, во многих случаях, дело обстоит так, что игроки делают ходы поочерёдно. Такие игры называются последовательными играми. Для их описания больше всего подходит развёрнутая форма игры, т.е. ее представление в виде де­рева игры.

Рассмотрим в качестве примера последовательную игру двух участников. Пусть первый ход принадлежит первому игроку, который имеет две стратегии; второй участник ходит вторым и имеет три стратегии. Дерево этой игры изображено на рис. 1:

Рисунок 1

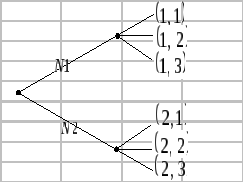
В данной игре первый игрок может оптимизировать свой выигрыш, проводя следующие вычисления. Сравниваются три исхода (1,1), (1,2) и (1,3). Пусть наибольшее значение выигрыша второго игрока достигается при исходе (1,2). Аналогично сравниваются три исхода (2,1), (2,2) и (2,3). Пусть наибольшее значение выигрыша второго игрока достигается при исходе (2,3). Тогда второй игрок, действуя рационально, в ответ на первую стратегию первого игрока выберет стратегию, при которой реализуется исход (1,2) а в ответ на вторую стратегию первого игрока выберет стратегию, при которой реализуется исход (2,3). Таким образом, первый игрок приходит к выводу, что если он выберет первую стратеги, то его выигрыш составит , а если он выберет вторую стратегию, то выигрыш будет ра­вен. Если, то первому игроку выгоднее придерживаться первой стратегии, а если, то первому игроку выгоднее придерживаться второй стратегии.

Данный тип оптимальности называется оптимальностью по Штакельбергу.

Исход игры называется равновесием по Штакельбергу, а страте­гииипервого и второго игроков соответственно называются оптимальными по Штакельбергу, если, гдеопределяется из уравнения