Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 408
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Обратная задача.
Задано:
-
геометрические размеры магнитной цепи; -
характеристики магнитных материалов; -
намагничивающая сила обмотки F. Найти: магнитный поток Ф .
Использовать непосредственно формулу (10.5) нельзя, т.к. зависит от Ф .
Rмсамо нелинейно
Такие задачи решают методом последовательных приближений. Для этого:
-
задаются рядом произвольных значений магнитного потока в цепи; -
так же, как и при решении прямой задачи для каждого из этих значений потока находят величину намагничивающей силы обмотки; -
по полученным данным строят кривую Ф(F) .
По кривой зависимости
Ф(F)
для заданного по условию задачи значения
намагничивающей силы F находят требуемую величину магнитного потока Ф.
-
Расчет разветвленных магнитных цепей
Различают симметричные и несимметричные магнитные цепи.
Симметричныемагнитныецепи.
Если разветвленную магнитную цепь можно представить в виде двух независимых частей, то это не изменит условий ее работы, а магнитные потоки ее симметричных частей будут иметь одну и ту же величину. В связи с этим достаточно провести расчет одной половины симметричной магнитной цепи согласно методике предыдущего параграфа.
Несимметричныемагнитныецепи.
Такой расчет основан на использовании законов Кирхгофа для магнитных цепей и аналогичен расчету разветвленных электрических цепей с нелинейными элементами.
Первыйзакон Кирхгофа для магнитной цепи. Алгебраическая сумма магнитных потоков узла равна нулю:
Ф 0 .
Рассмотрим пример на рис.9.8. По первому закону Кирхгофа
Ф1 Ф2 Ф3 0 .
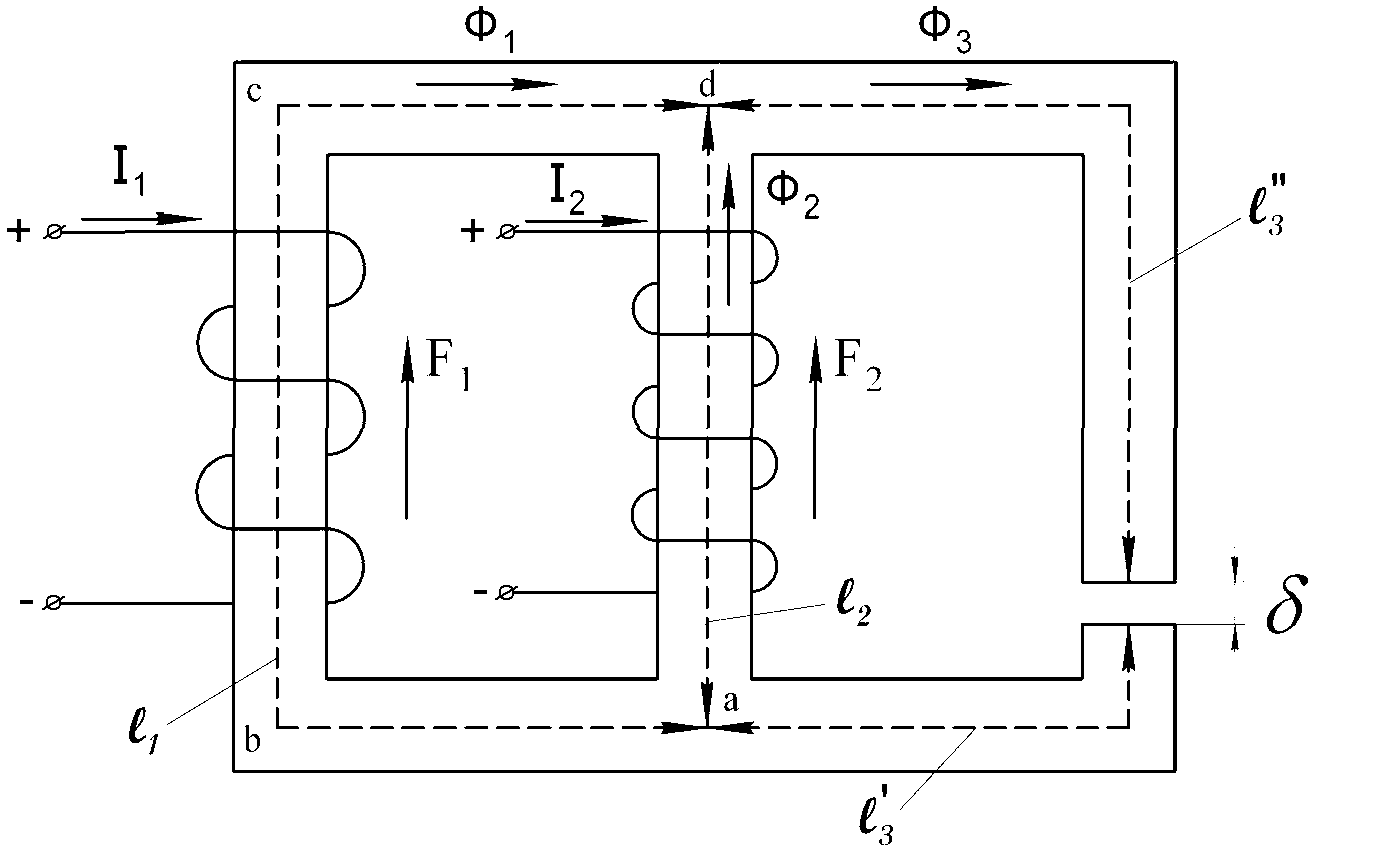
Рис.9.8
Применим закон полного тока к контуру a-b-c-d-a (обход контура выберем по часовой стрелке):
F1 F2 H1 l1 H2 l2 . (9.6)
Произведение
H l
взято с минусом, т.к.
H2 (совпадающее с направлением
2 2
Ф2 ) противоположно направлению обхода.
Заменим в (9.6) Н1 и Н2 на
H1
Ф1
S μ
и H2
Ф2 S μ
соответственно, получим
F1 F2
Ф1
l1 S1 μ1
Ф2
l2 S2 μ2
Ф1
Rм1
Ф2
1 1 2 2
Rм2 .
В общем виде второй закон Кирхгофа для магнитной цепи запишется
следующим образом Fk Фk Rмk.
Произведение Фk Rмkназывают магнитнымнапряжением(по аналогии с
I R
-
электрическим напряжением), Rk
- называется магнитным сопротивлением k-
го участка магнитной цепи.
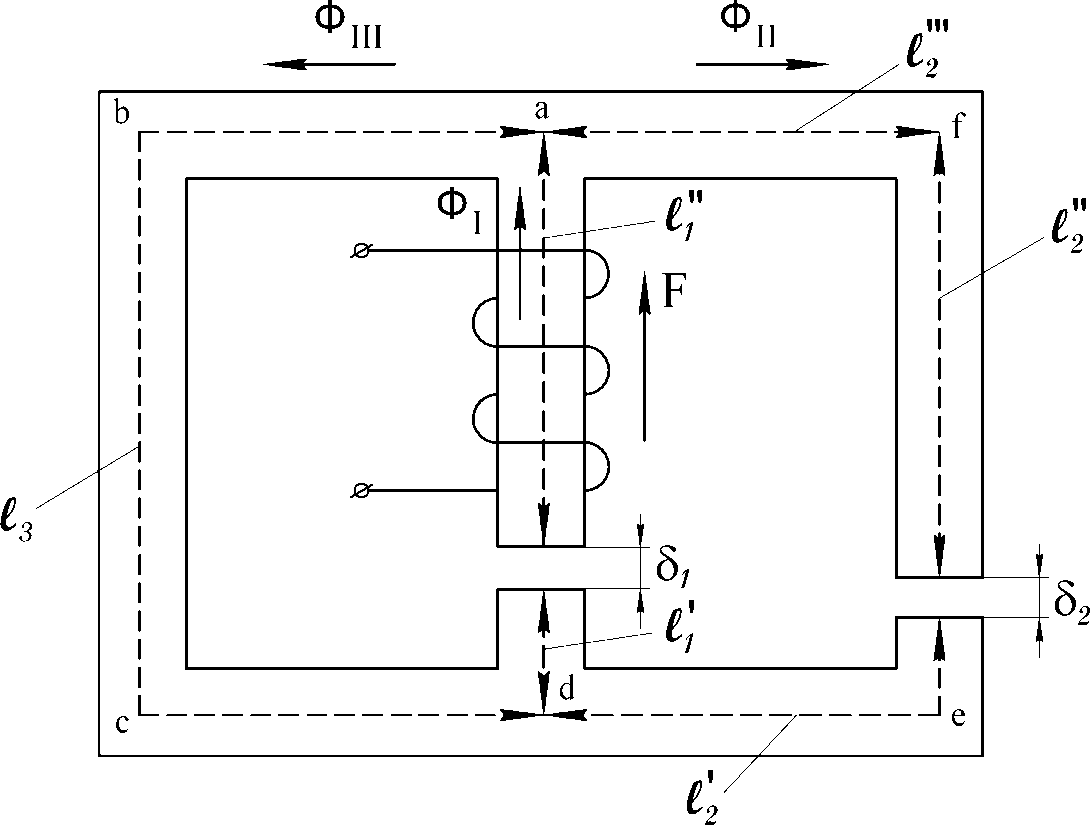
 Рассмотрим последовательность и порядок расчета несимметричной магнитной цепи с одной намагничивающей катушкой (рис.9.9).
Рассмотрим последовательность и порядок расчета несимметричной магнитной цепи с одной намагничивающей катушкой (рис.9.9).Рис.9.9 Рис.9.10
Задано:
-
геометрические размеры цепи; -
кривые намагничивания; -
намагничивающая сила обмотки F.
Требуется: определить магнитные потоки во всех участках цепи.
Обозначим магнитные сопротивления участков a-d, a-f-e-d и a-b-c-d
соответственно
RI,
RII
и RIII, а проходящие по ним потоки ФI, ФII
и ФIII.
Применим к узлу a и контурам a-f-e-d-a и a-b-c-d-a магнитной цепи первый и второй законы Кирхгофа
F ФI RI ФII RII;
I
F Ф R
I
ФIII
RIII;
Ф
Ф
I II
ФIII .
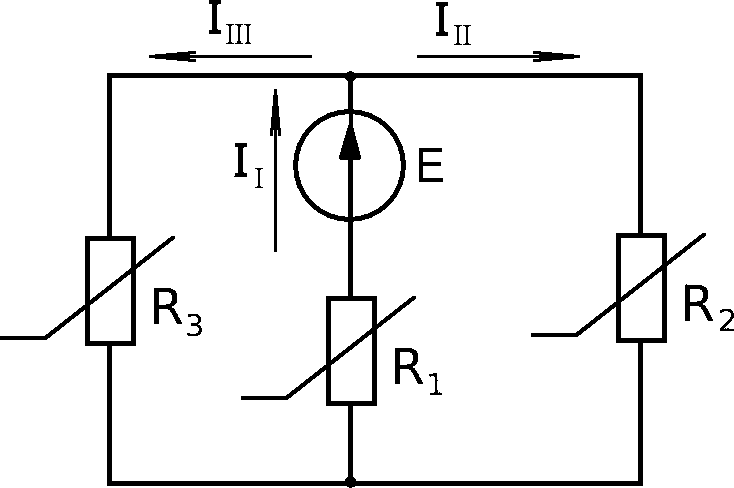
Аналогом этой магнитной цепи является нелинейная электрическая цепь на рис.10.10. Система уравнений по законам Кирхгофа для нее имеет вид
E II R1 III R2 ;
I
E I
R1 IIII
R3 ;
I
I
I II
IIII .
Как известно, решение этой системы производится графическим путем на
основе имеющихся ВАХ (находят неизвестные
II,
III,
IIII).
Аналогично определяют неизвестные величины потоков ФI, ФII, ФIII. Для этого:
-
задаются несколькими значениями магнитного потока Ф; -
для каждого значения Фопределяют соответствующую ему намагничивающую силу F ;
-
для каждой ветви строят график
Ф(F)
(так называемую вебер-амперную
характеристику). Пусть, например, это будут кривые 1, 2 и 3 соответственно для участков a-d, a-f-e-d и a-b-c-d (рис.9.11);
-
для двух параллельных ветвей a-b-c-d и a-f-e-d строят результирующую вебер-амперную характеристику 4, получаемую путем суммирования ординат кривых 2 и 3; -
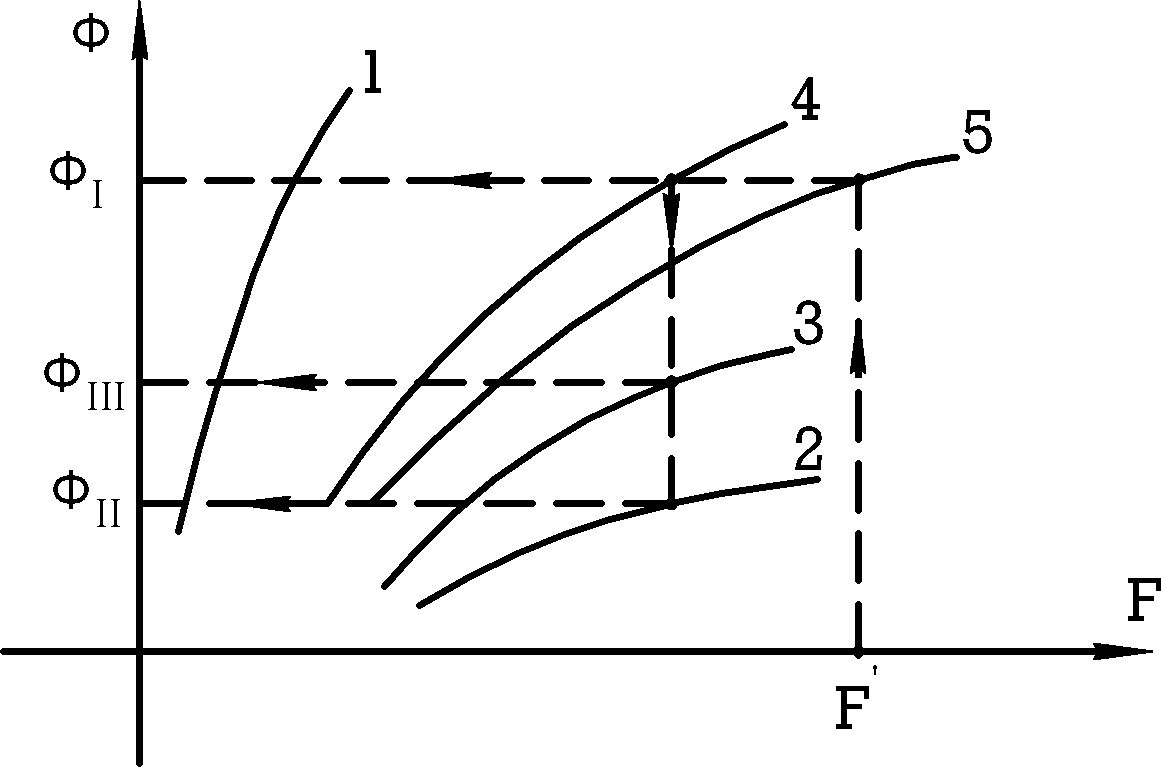 суммируя абсциссы кривых 1 и 4, получают результирующую вебер- амперную характеристику всей магнитной цепи 5 (рис.9.11).
суммируя абсциссы кривых 1 и 4, получают результирующую вебер- амперную характеристику всей магнитной цепи 5 (рис.9.11).
Рис.9.11
Пользуясь этой кривой нетрудно по заданному значению намагничивающей
силы F найти поток в неразветвленной части магнитной цепи, т.е. поток ФI. Части
этого потока ФII
и ФIII
можно найти с помощью кривых 2, 3 и 4. (см. рис.9.11).
- 1 ... 48 49 50 51 52 53 54 55 56
Катушка индуктивности с ферромагнитным сердечником
У катушки без сердечника магнитный поток
Ф B S
пропорционален
магнитной движущей силе
F I w, а зависимость Ф(I)
является линейной.
При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).
Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на
несколько порядков выше магнитной проницаемости воздуха
μ0 . Значит,
одинаковый магнитный поток в катушке с магнитопроводом можно получить при
значительно меньшей намагничивающей силе F I w.
Схема замещения реальной катушки индуктивности имеет вид рис.9.12.
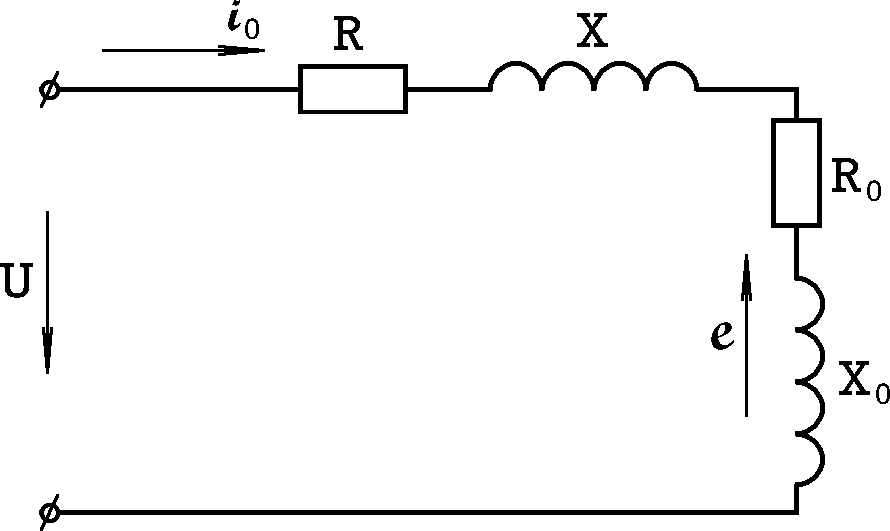
Здесь i0
Рис.9.12 Рис.9.13
-
 ток катушки; R- активное сопротивление проводов катушки;
ток катушки; R- активное сопротивление проводов катушки;
x ω L
-
индуктивное сопротивление катушки;
R0 - активное сопротивление,
обусловленное потерями мощности в катушке
R PM;
0 I2
x0 - индуктивное
сопротивление, обусловленное основным магнитным потоком.
По второму закону Кирхгофа
U R I
-
jx I
-
E .
0
0
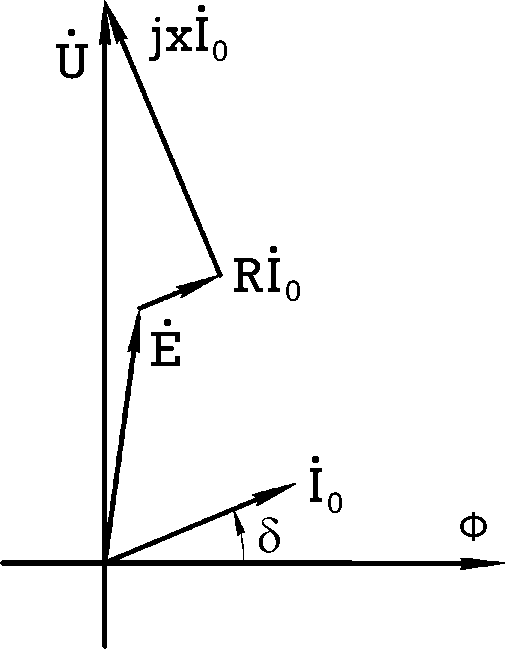
Векторная диаграмма, построенная в соответствии с данным уравнением,
имеет вид (рис.10.13). Так как
e dФ, то Ф отстает по фазе от E на
dt
π. Кроме того,
2
0
Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как
зависимость
B(H)
– нелинейная, следовательно нелинейной будет и зависимость
Ф(i0 ) (рис.9.14).
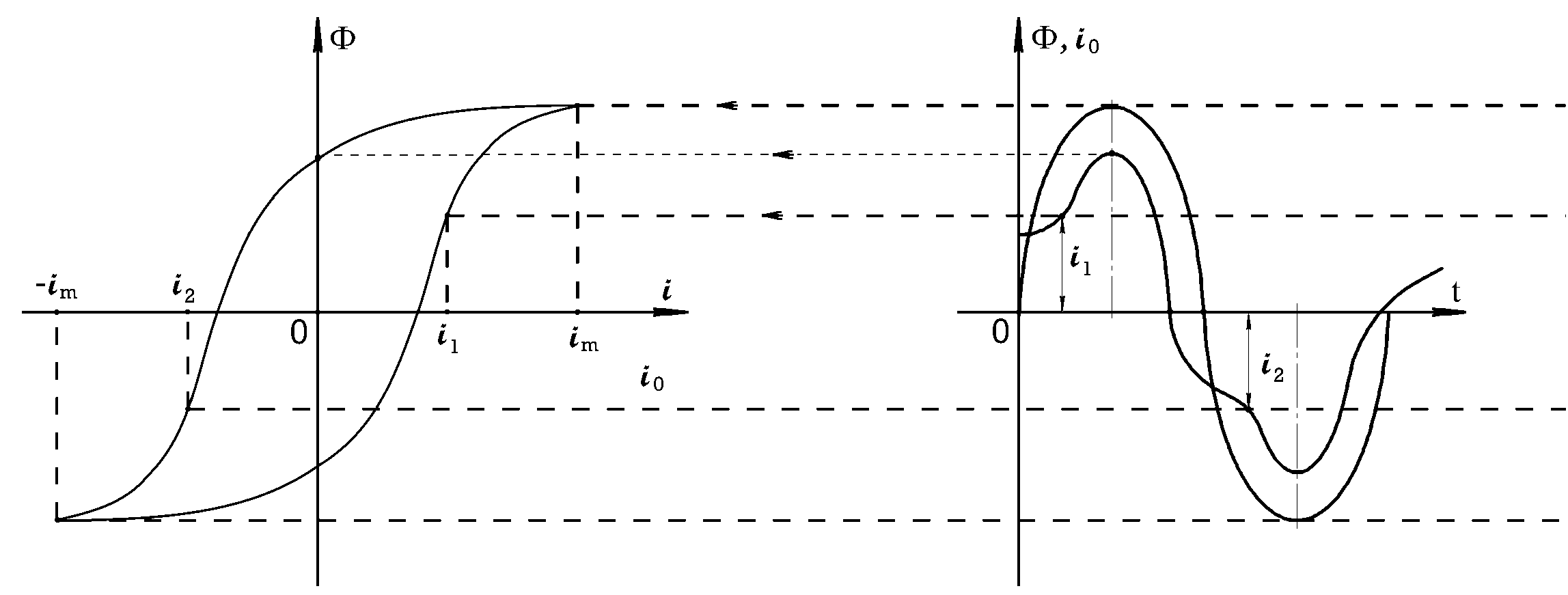
Так как напряжение зависимость Ф(t) .
u(t)
Рис.9.14
синусоидальное, значит синусоидальной будет и
Но из-за нелинейности
B(H)
ток катушки с сердечником
i0 (t)
будет
несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока.
Из рис. 9.14 видно, что ток i0
опережает по фазе поток Фна гистерезисный
угол δ(ток достигает нуля раньше магнитного потока).
Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону Ома
Ф F,
Rм
где
Rмопределяются, в основном, сопротивлением воздушного зазора.
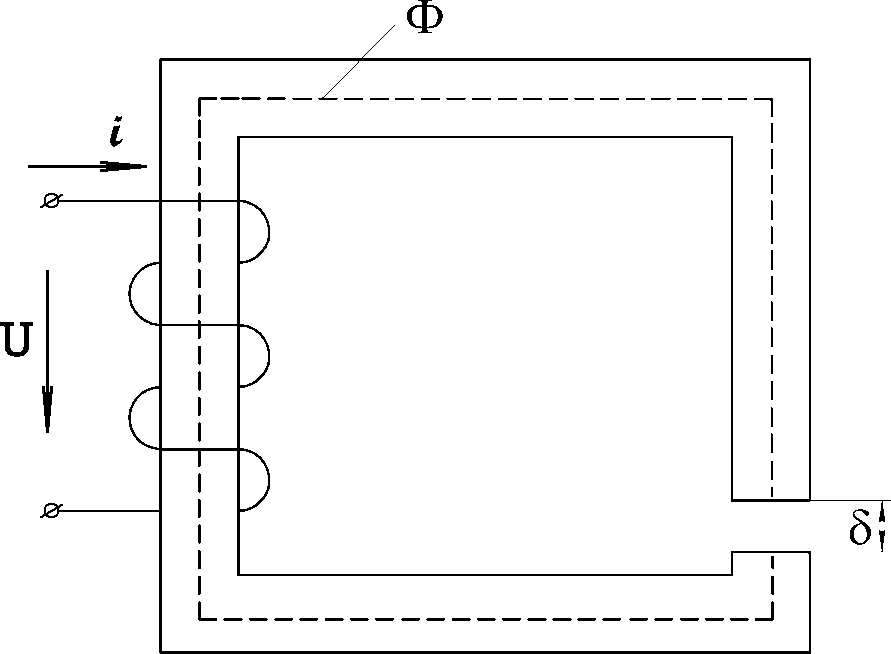
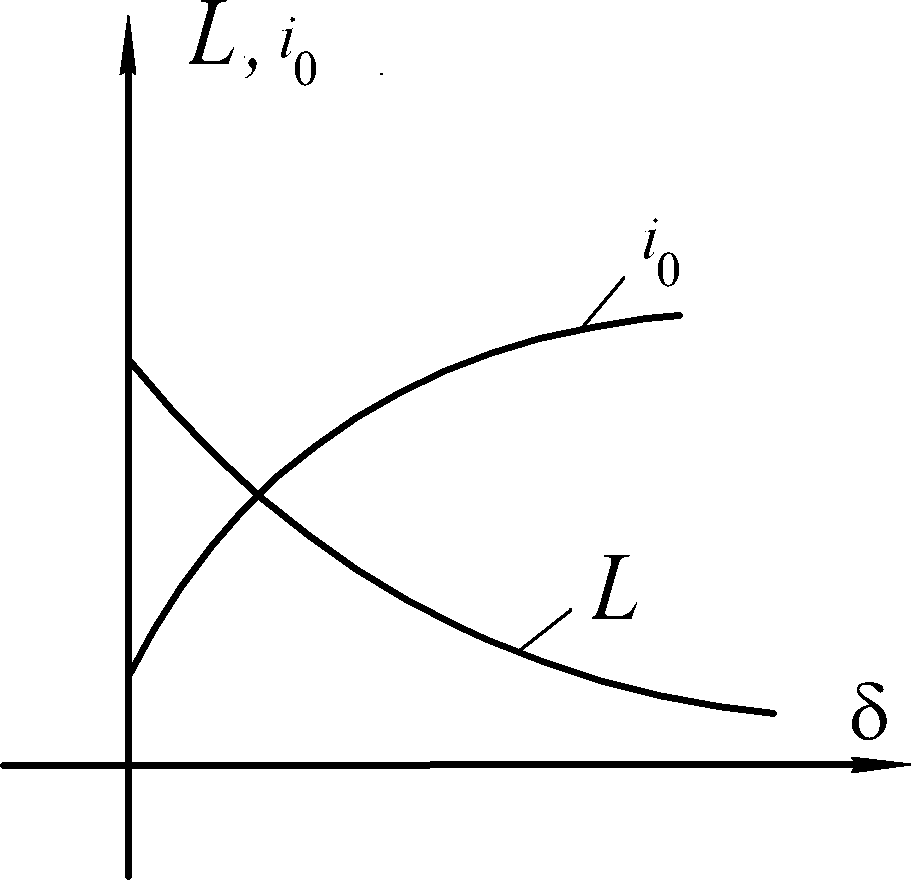
Рис. 9.15 Рис.9.16
Увеличение воздушного зазора увеличивает
Rм, а значит должно уменьшить
поток Ф. Но этого не происходит, т.к. из формулы
U 4,44 f w Фm
следует, что
Фm
U
4,44 f w
, т.е. величина потока зависит только от действительного значения
питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая
сила
I w
до значения, при котором поток Ф(а значит и отношение
F) остается
Rм
постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное
сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).
Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с.
-
Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил.
-
Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000.
1 ... 48 49 50 51 52 53 54 55 56
Катушка индуктивности с ферромагнитным сердечником
У катушки без сердечника магнитный поток
Ф B S
пропорционален
магнитной движущей силе
F I w, а зависимость Ф(I)
является линейной.
При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).
Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на
несколько порядков выше магнитной проницаемости воздуха
μ0 . Значит,
одинаковый магнитный поток в катушке с магнитопроводом можно получить при
значительно меньшей намагничивающей силе F I w.
Схема замещения реальной катушки индуктивности имеет вид рис.9.12.

Здесь i0
Рис.9.12 Рис.9.13
-
 ток катушки; R- активное сопротивление проводов катушки;
ток катушки; R- активное сопротивление проводов катушки;
x ω L
-
индуктивное сопротивление катушки;
R0 - активное сопротивление,
обусловленное потерями мощности в катушке
R PM;
0 I2
x0 - индуктивное
сопротивление, обусловленное основным магнитным потоком.
По второму закону Кирхгофа
U R I
-
jx I -
E .
0
0
Векторная диаграмма, построенная в соответствии с данным уравнением,
имеет вид (рис.10.13). Так как
e dФ, то Ф отстает по фазе от E на
dt
π. Кроме того,
2
0
Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как
зависимость
B(H)
– нелинейная, следовательно нелинейной будет и зависимость
Ф(i0 ) (рис.9.14).
Так как напряжение зависимость Ф(t) .
u(t)
Рис.9.14
синусоидальное, значит синусоидальной будет и
Но из-за нелинейности
B(H)
ток катушки с сердечником
i0 (t)
будет
несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока.
Из рис. 9.14 видно, что ток i0
опережает по фазе поток Фна гистерезисный
угол δ(ток достигает нуля раньше магнитного потока).
Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону Ома
Ф F,
Rм
где
Rмопределяются, в основном, сопротивлением воздушного зазора.

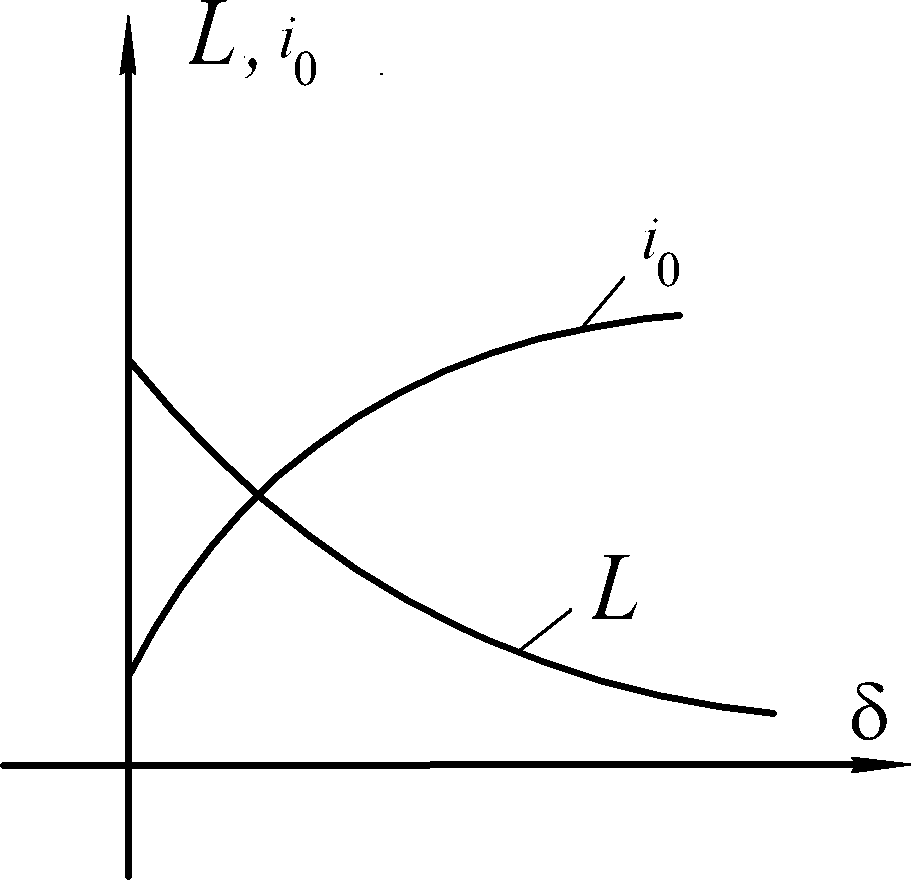
Рис. 9.15 Рис.9.16
Увеличение воздушного зазора увеличивает
Rм, а значит должно уменьшить
поток Ф. Но этого не происходит, т.к. из формулы
U 4,44 f w Фm
следует, что
Фm
U
4,44 f w
, т.е. величина потока зависит только от действительного значения
питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая
сила
I w
до значения, при котором поток Ф(а значит и отношение
F) остается
Rм
постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное
Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с.
Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил.
Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000.