Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 391

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56

Индуктивность


Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.



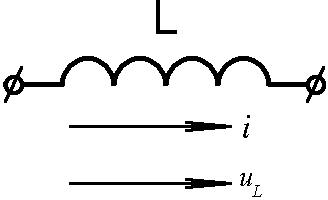
Рис.1.10

Обозначение индуктивности показано на рис. 1.10.

Если по проводнику пропустить ток, то вокруг него создается магнитный поток Ф. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен

w Ф,

где Ф– магнитный поток, создаваемый одним витком; w – число витков.

По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током катушки



Индуктивность измеряется в генри

L ψ.

i

1 Гн 1 Bб.

1 А

Поток сцепления катушки индуктивности равен:

L i.

В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции:

e d ,

L dt

(знак “–” потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС).

Напряжение на индуктивности уравновешивает ЭДС и может быть записано в

виде:
u e

d Ldi.



L L dtdt

Мгновенная мощность, поступающая в катушку индуктивности равна

p uL

i L i di.

dt

Энергия, запасаемая в катушке индуктивности равна

ttdi

L i2 .

wM pdt L i dt dt 2

0 0

        1. Взаимная индуктивность





Она характеризует свойство одного элемента с током i1

создавать магнитное

поле, частично сцепляющиеся с витками w2

другого элемента.

Коэффициент взаимной индуктивности определяется по формуле:

М 12


12
i2

21 ,

i1

где

– поток сцепления 1-го контура, вызванный током 2-го контура (аналогично


21
 ). Измеряется в Гн.

        1. 1   2   3   4   5   6   7   8   9   ...   56

Емкость



Емкостью называется идеализированный элемент электрической цепи по своим свойствам приближающийся к конденсатору, в котором накапливается энергия электрического поля.

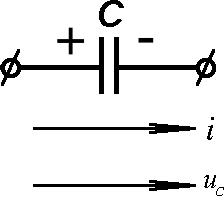Обозначение емкости показано на рис. 1.11. Величина Cопределяется из выражения

C q,

uC

где q– величина заряда в емкости, uC

– напряжение

Рис.1.11

на ее зажимах. Единица измерения емкости – фарада, Ф. Емкости бывают линейными и нелинейными.

Из определения тока имеем:

i dq CduC.

dtdt

Преобразуя это выражение можно получить выражение для напряжения

на емкости

u 1

CC

t

idt.



Мгновенная мощность, поступающая в емкость

pC uC

i uC

CduC.

dt

Энергия, запасаемая емкостью за интервал времени [0, t)

ttdu

C u2


Ý
w pCdt uCCCdtC.

0 0 dt 2

      1. Понятие схемы замещения электрических цепей. Условное положительное направление токов, ЭДС и напряжений в цепи



Для упрощения анализа реальной цепи ее представляют математической моделью – набором идеальных элементов.

Графическое изображение цепис помощью идеальных элементов, параметры которых являются параметрами замещаемых элементов, называют схемой замещения цепи.

Идеальные элементы вводят в схему замещения для того, чтобы учесть явления, которые характеризуют их параметры. Например, для учета процесса поглощения энергии элементом цепи в схему замещения вводят сопротивление. Индуктивные и емкостные элементы вводят тогда, когда хотят учесть влияние электрических и магнитных полей.

Для однозначности описания процессов, происходящих в элементах цепи, необходимо знать не только величины токов и напряжений на них, но также их направления. В начале анализа или расчета электрической цепи их направление неизвестно. В связи с этим положительное направление тока и напряжения

выбирается произвольно (стрелками или индексами

iab). Если в процессе расчета

цепи оказалось, что значения величинU, u, I, iположительны, то следовательно, их

действительные направления в этот момент времени совпадают с направлениями, указанными на схеме стрелками. В противном случае истинные направления

U, u, I, i– противоположны условно выбранным.

Из физики известно, что за положительное направление тока принято направление движения положительных зарядов, за положительное направление ЭДС – направление действия “сторонних” сил на положительный заряд, за положительное направление напряжения – направление убывания потенциала.

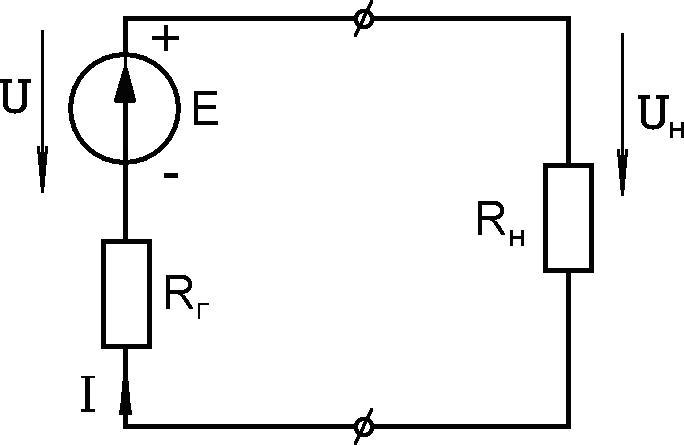Так как положительные заряды в источнике ЭДС движутся в направлении действия “сторонних” сил, а в приемнике – в направлении убывания потенциала, то положительное направления тока и ЭДС источника, тока и напряжения приемника совпадают (рис.1.12).
Рис.1.12

Положительное направление напряжения на внешних зажимах источника противоположному направлению тока источника (рис.1.12). Это нужно учитывать при выборе условного положительного направления данных физических величин.

      1. 1   2   3   4   5   6   7   8   9   ...   56

Основные определения, относящиеся к топологии электрической цепи



Схемой электрической цепи называется графическое изображение электрической цепи, показывающие соединение отдельных ее участков и отражающее свойства рассматриваемой цепи.

Любая электрическая цепь состоит из ветвей и узлов.

Ветвью называется участок цепи, в любой точке которого ток в данный момент времени имеет одно и то же значение. В ветвь может входить любое число последовательно включенных элементов.

Узломназывается местное соединение трех или большего числа ветвей.

Контуром электрической цепи называется любой путь, проходящий по нескольким ветвям.

Графом электрический цепи называется изображение схемы электрической цепи, в которой ветвь изображается линией, источники напряжения закорочены, а источники тока разомкнуты.

Различают контуры зависимые и независимые. Для того, чтобы дать определение независимого контура, прежде сформулируем понятие дерева цепи.

Дерево цепи (дерево графа) есть такая совокупность элементов цепи, когда при движении вдоль элементов цепи можно от любого узла исходной цепи пройти к любому другому узлу цепи, кроме рассматриваемого.

На рис. 1.13 изображена схема, а на рис.1.14,а и рис.1.14,б – ее возможные деревья.



Рис.1.13 Рис.1.14,а Рис.1.14,б

Элементы, которые отбрасываются при образовании дерева цепи, называются

соединительнымиэлементами.

Число независимых контуров электрической цепи равночислу соединительных элементов данной цепи.

Смотрите также файлы