Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 409

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56


произведение

Ek Ik

берется со знаком плюс, а в противном случае – со знаком

минус); n– общее число источников ЭДС;

UJ J

  • мощность, выдаваемая в цепь


k
U
k
k
источниками тока, а J– напряжение на источнике тока (направлено навстречу

стрелке источника тока); m– общее число источников тока;

I2 R

  • мощность,

kk

поступающая в сопротивление

Rk; N– общее число сопротивлений в цепи.



    1. 1   ...   9   10   11   12   13   14   15   16   ...   56

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ


На практике часто встречаются цепи, параметры элементов которых нелинейно зависят от тока. Такие элементы и содержащие их цепи называются нелинейными.

Вообще говоря, большинство элементов электрических цепей нелинейно (например, сопротивление проводника с ростом температуры увеличивается). Однако их принимают за линейные, если в рабочем диапазоне изменений токов их вольт – амперные характеристики линейны.

Различают нелинейные элементы с симметричными (1) и не симметричными

(2) характеристиками относительно осей координат (рис.4.1).



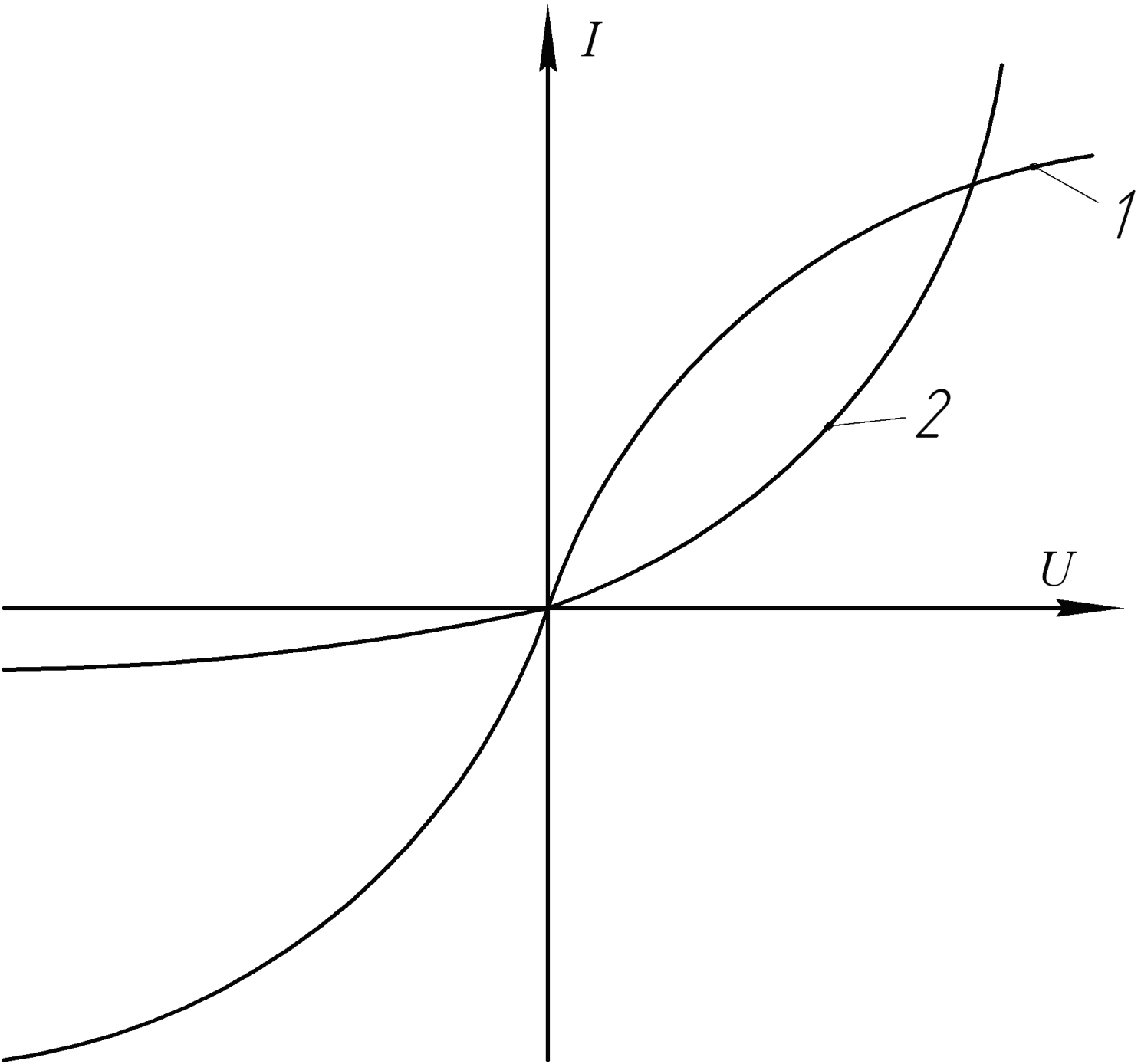
Рис.4.1

Сопротивление нелинейных элементов с симметричными характеристиками не зависят от направления тока. Нелинейные элементы с несимметричной характеристикой часто используются в цепях переменного тока в качестве выпрямителей или стабилизаторов напряжения и тока. На рис.4.1 изображена вольт-амперная характеристика (ВАХ) полупроводникового диода (кривая 2), которая несимметрична.

Нелинейные элементы, ВАХ которых изменяются под воздействием хотя бы одной из влияющих величин, называются управляемыми

(например, электровакуумные и полупроводниковые триоды).

Существует два основных метода расчета нелинейных цепей: графический и аналитический.

      1. Графический метод расчета (метод эквивалентных преобразований)


При расчете нелинейных цепей данным методом последовательность операций сохраняется примерно той же, что и при расчете линейных цепей, только вместо сложения или вычитания отдельных напряжений и токов, производится сложение или вычитание абсцисс и ординат соответствующих ВАХ. Рассмотрим пример последовательного соединения линейного и нелинейного сопротивлений (рис.4.2).



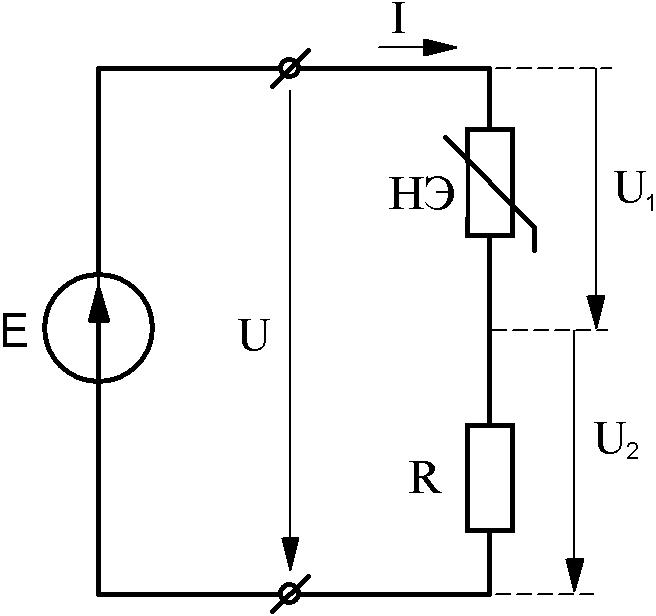
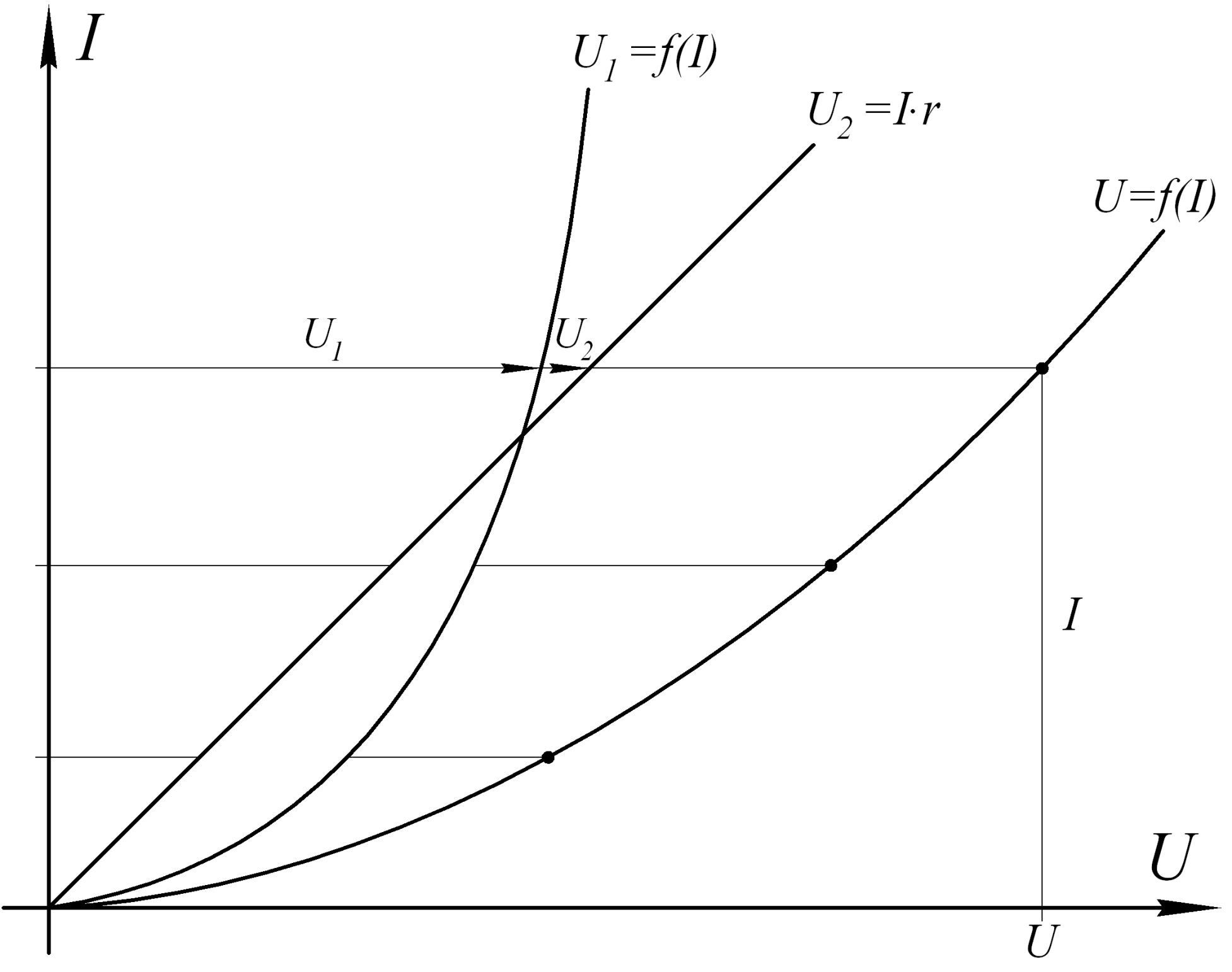
Рис.4.2 Рис.4.3

Для того, чтобы найти ток Iи частичные напряжения U1
и U2
нужно

построить ВАХ цепи в целом, т.е. характеристику U

f(I) .

Очевидно, что

U U U, а некоторому току Iсоответствует некоторые


1 2
напряжения U1 и U2 , которые определяются как абсциссы двух точек ВАХ

линейного и нелинейного элементов цепи для данного неизменного тока I(рис.4.3). Сложив эти абсциссы, получим напряжение U, соответствующее силе тока I

(фактически, получим одну точку результирующей ВАХ

U f(I) ). Путем

подобного сложения можно получить ВАХ U

f(I)

всей цепи в целом, пользуясь

которой можно получить и частичные напряжения U1, U2и силу тока Iдля любого заданного значения напряжения U .

Для определения режима работы изображенной выше нелинейной цепи, можно применить графическое вычитание (опрокидывание характеристики).

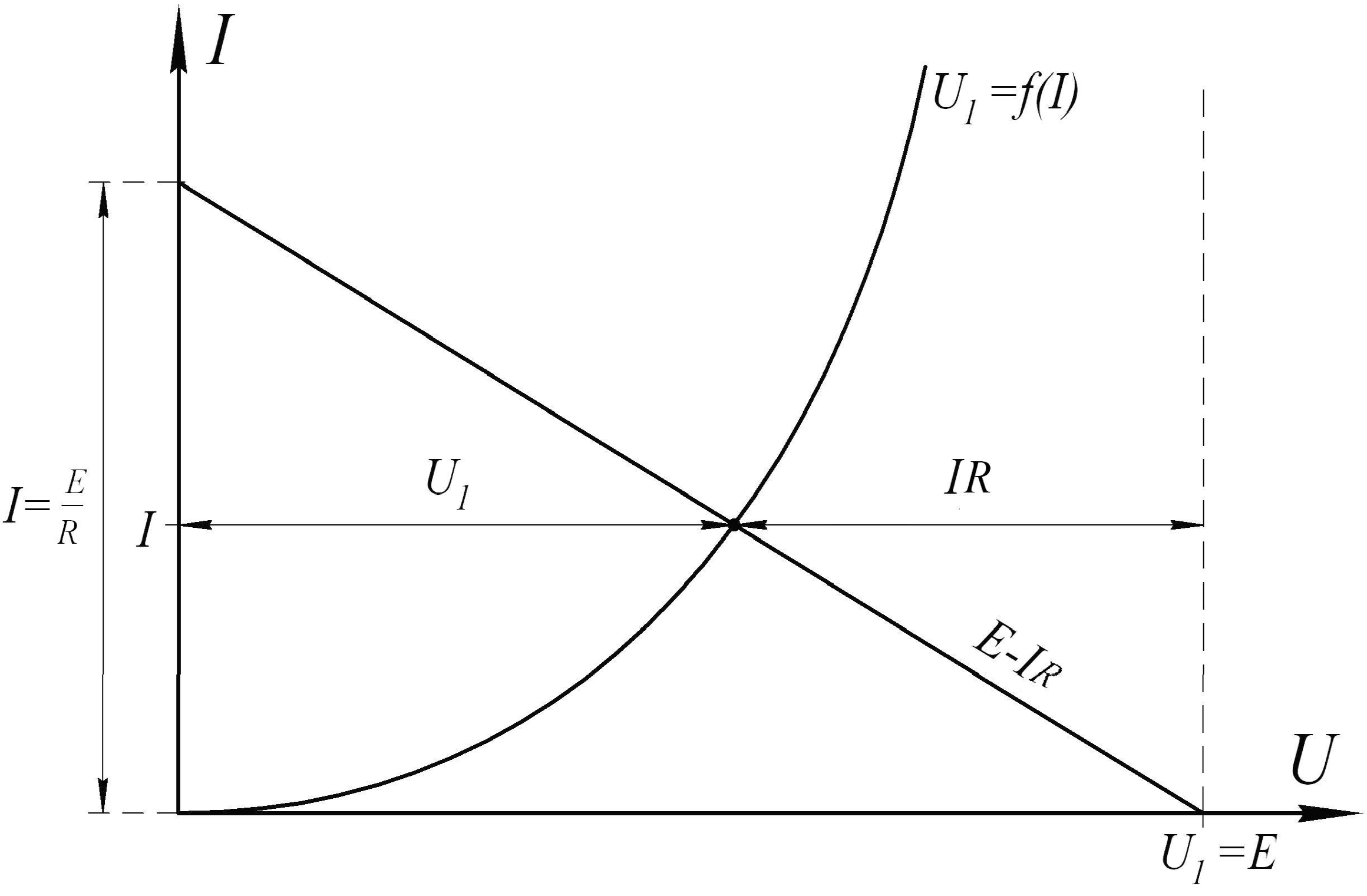Например, на зажимах нелинейного элемента действует

напряжение U1 EI R.

В системе координат

U1 , I

– это уравнение прямой линии, которая пересекает ось абсцисс в

точке точке

U E, а ось ординат – в


1
IE.

R


Рис.4.4

Пересечение ВАХ нелинейного

элемента и постоянной нагрузочной прямой дает рабочую точку (рабочий режим цепи).

Графический расчет параллельного соединения нелинейных элементов ведется аналогично. Используя ВАХ двух параллельно соединенных

сопротивлений, строится характеристика разветвления

I1

f(Up ) . Для этого

фиксируются напряжения (т.к. при параллельном соединении Up=const) и определяются соответствующие им токи ветвей I2 и I3 (ординаты характеристик параллельных ветвей).Затем ординаты складываются, т.е. находятся токи I1=I2 + I3

для каждого из зафиксированных значений напряжений UP

и строится

результирующая характеристика

I1 I2 I3

f(Up) .

Графический расчет смешанного соединения ведется в том же порядке, в каком порядке ведется аналитический расчет смешанного соединения линейных сопротивлений.

      1. 1   ...   10   11   12   13   14   15   16   17   ...   56

Аналитический метод расчета



Из числа аналитических методов расчет нелинейных цепей наиболее широкое применение имеет метод линеаризации характеристик.

Если в пределах некоторого участка нелинейная характеристика элемента может быть приближенно заменена прямой, то в этих пределах отношение

приращений величин U

и I

есть величина постоянная, т.е.

U const

I

или

du const. Здесь

du R

- дифференциальный параметр цепи ( дифференциальное



didi

сопротивление).

Отношение

uR

называется статическим сопротивлением.

iC

Для линейной ВАХ

R RC.

Суть расчета: пользуясь дифференциальными параметрами можно составить эквивалентную электрическую схему для нелинейного элемента цепи и, таким образом, создается возможность рассчитывать цепь как линейную при условии, что изменения режима работы цепи не выходят за пределы линейного участка характеристики.

Пусть характеристика нелинейного сопротивления имеет вид рис.4.5.


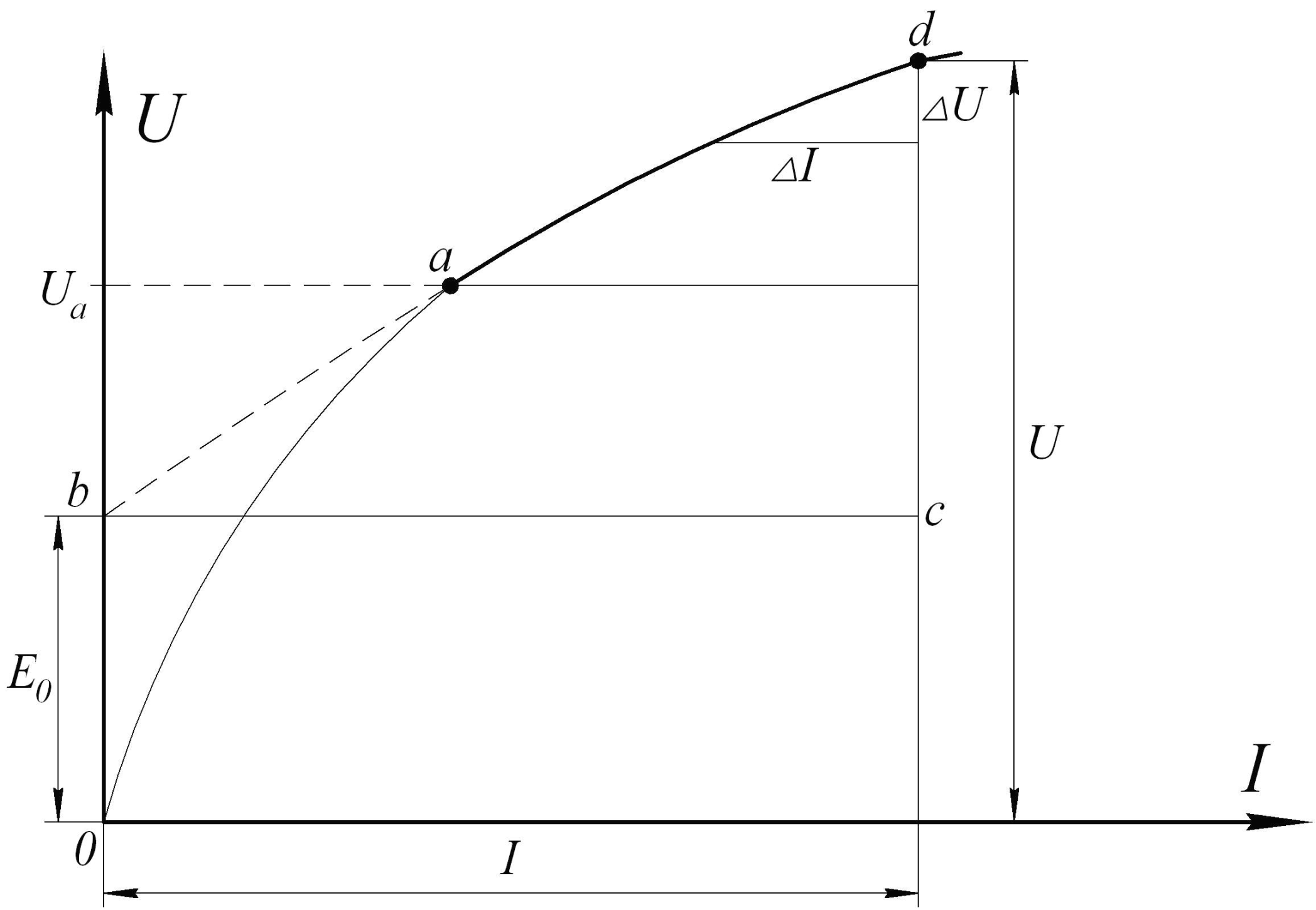
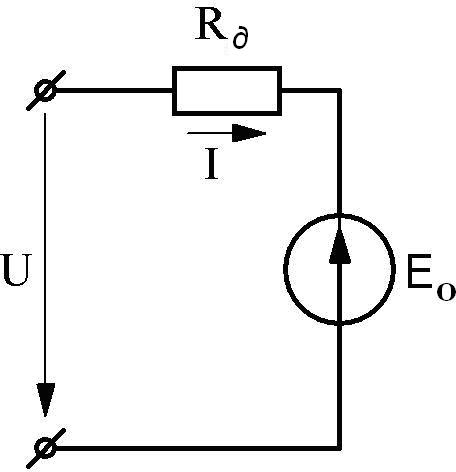
Рис.4.5 Рис.4.6

Характеристика выше точки a приблизительно линейная. Продолжим эту прямую до пересечения с осью ординат. Точка пересечения данной прямой и оси

Смотрите также файлы