Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 371
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Конденсатор в цепи синусоидального тока
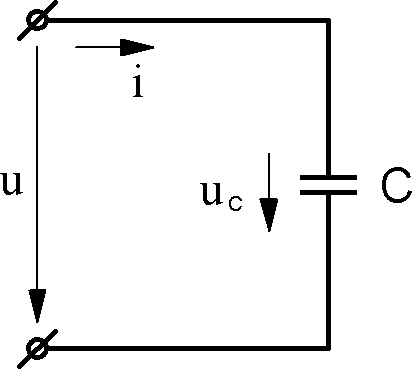 Пусть к идеальному конденсатору подведено напряжение
Пусть к идеальному конденсатору подведено напряжениеu
uС UCm sin(ω tψ)
.
U
.
Cm
ejωt.
Ток в конденсаторе равен:
i C duC
dt
. j ω CU
ejωt
ω CU Cm
ej(ωt90) ;
.
Cm
Рис.5.20
или
i ω CU
sin(ω tψ
-
90) .
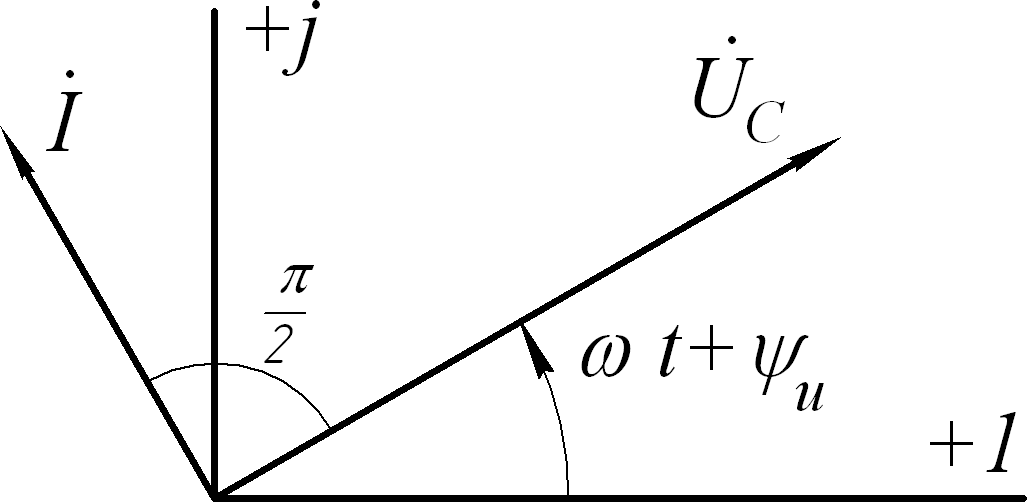
Cm
u
Следовательно, токчерез конденсаторопережаетпофазе
напряжениена90 .
Векторная диаграмма представлена на рис.5.21.
Перепишем выражение для тока:
Рис.5.21
i UCm
1
ω C
sin(ω tψu
-
90).
Здесь
1
ω C
1
2 π f C
xC
- называется реактивнымсопротивлением
конденсатора или просто емкостным сопротивлением; сопротивления.
-
j xC
- комплекс емкостного
Мгновенное значение мощности в цепи с конденсатором:
pC uC
i UCm
Im
sin ω tψu
sinω tψ
u
π U
2
C
Isin2 ω t 2 ψu.
ψ
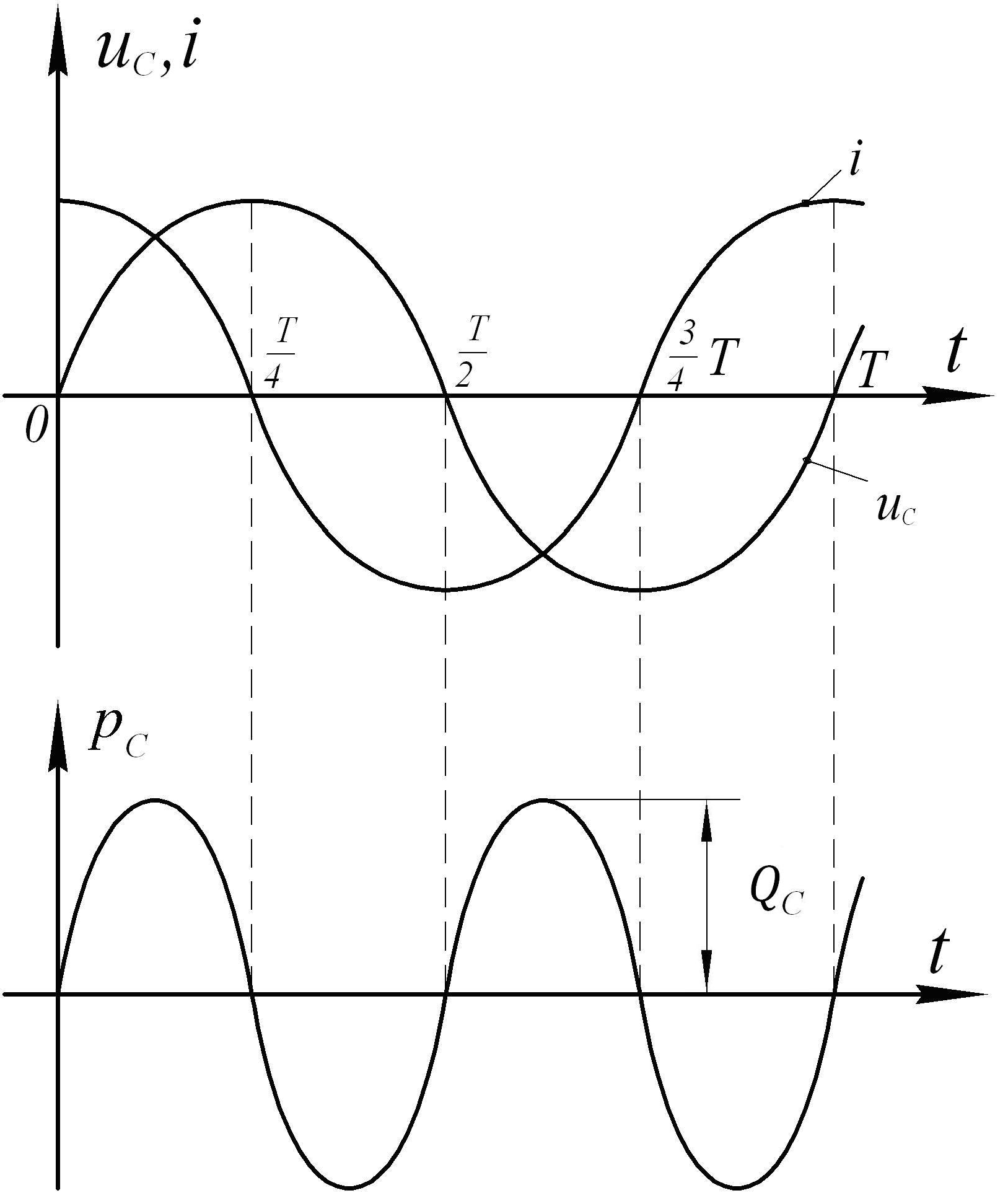
Изобразим графики зависимостей
uC, iи
pCот времени (рис.5.22), а для
простоты возьмем
0 .
u
Здесь также наблюдается колебательный процесс мощности. Следовательно, среднее значение мощности за период равно нулю, т.е.
T
1
T
PС pCdt 0 .
0
 От 0 до
От 0 доTконденсатор заряжается, т.е.
4
накапливает энергию, поступающую от источника в виде энергии электрического поля
конденсатора. За время от
Tдо
4
Tконденсатор
2
разряжается, и энергия электрического поля конденсатора возвращается в источник и т.д.
C
C
Амплитуда колебания мощности в цепи с конденсатором называется реактивной емкостной мощностью:
Рис.5.22
Q x
I2 .
- 1 ... 22 23 24 25 26 27 28 29 ... 56
Комплексная мощность
Если известны напряжение и ток в цепи переменного тока, имеющие
комплексные выражения
U Um
 2
2
ejψu
и I
Im e
jψi, а также сдвиг фаз между ними
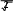 φψuψi, то выражение полной комплексной мощности в данной цепи
φψuψi, то выражение полной комплексной мощности в данной цепи
определяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид:
S
U I*
U e
jψu
I e
jψi
U I e
j(ψu
ψi)
S
U I ejφ U I cosφ
jU I sinφ P j Q,
где
P ReU I* , а Q ImU I* ;
– полная мощность ВА; P– активная
мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр.
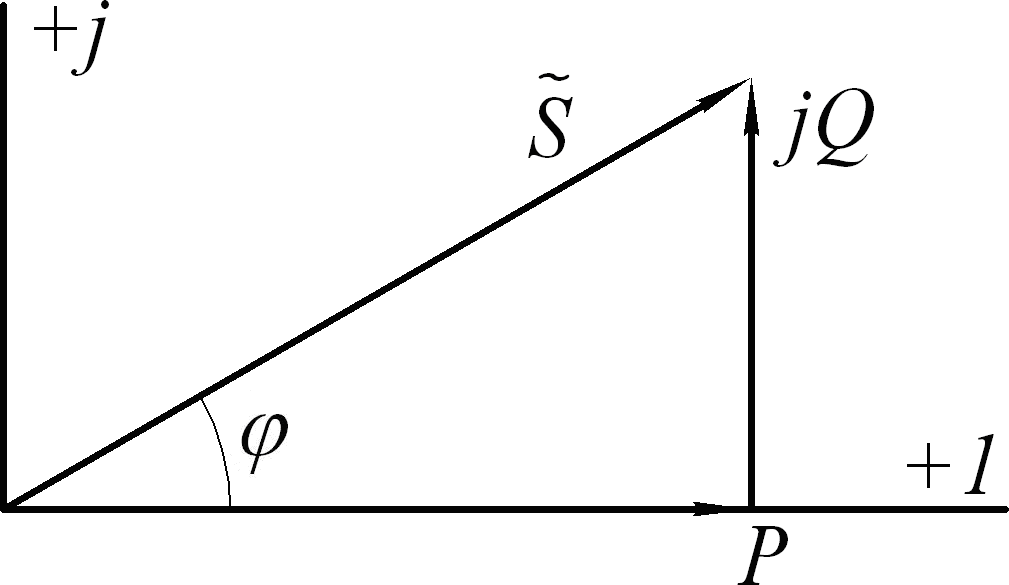
Рис. 5.23
Треугольник мощностей на комплексной плоскости показан на рис. 5.23.
Этот случай соответствует положительному значению реактивной мощности Q .
-
1 ... 23 24 25 26 27 28 29 30 ... 56
Комплексная мощность
Если известны напряжение и ток в цепи переменного тока, имеющие
комплексные выражения
U Um
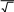 2
2 ejψu
и I
Im e
jψi, а также сдвиг фаз между ними
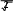 φψuψi, то выражение полной комплексной мощности в данной цепи
φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид:
S
U I*
U e
jψu
I e
jψi
U I e
j(ψu
ψi)
S
U I ejφ U I cosφ
jU I sinφ P j Q,
где
P ReU I* , а Q ImU I* ;
– полная мощность ВА; P– активная
мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр.
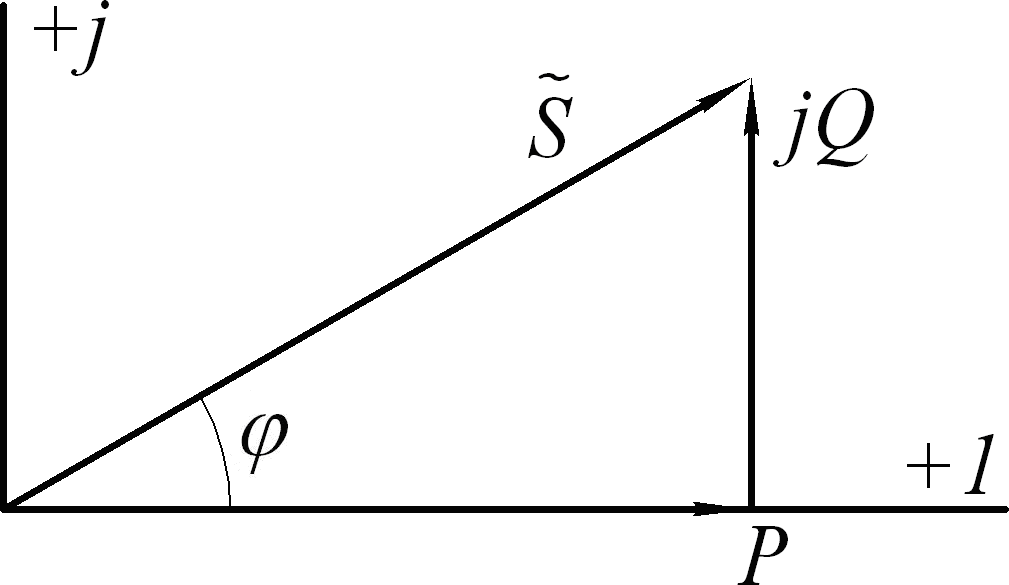
Рис. 5.23
Треугольник мощностей на комплексной плоскости показан на рис. 5.23.
Этот случай соответствует положительному значению реактивной мощности Q .
- 1 ... 23 24 25 26 27 28 29 30 ... 56
Последовательное соединение RL и RC
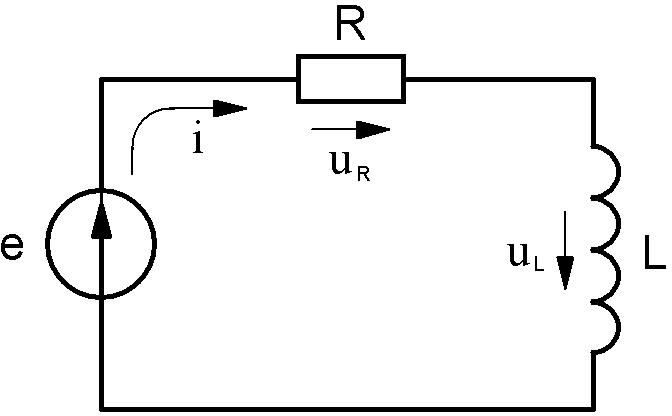 Пусть задана цепь (рис.5.24).
Пусть задана цепь (рис.5.24).По второму закону Кирхгофа запишем
R
e u
-
u, или
e i R Ldi.
dt
L
В комплексном виде это уравнение может быть записано:
или
I (R
Рис.5.24
j ω L) E ,
I Z E ,
I R
j ω L I E ,
где
R j ω L Z
z ejφ– комплексное сопротивление данной цепи.
Выражение для модуля полного сопротивления цепи имеет вид
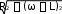 z .
z .Очевидно, что угол сдвига по фазе между общим током I и E можно определить по формуле:
φ arctgω L.
R
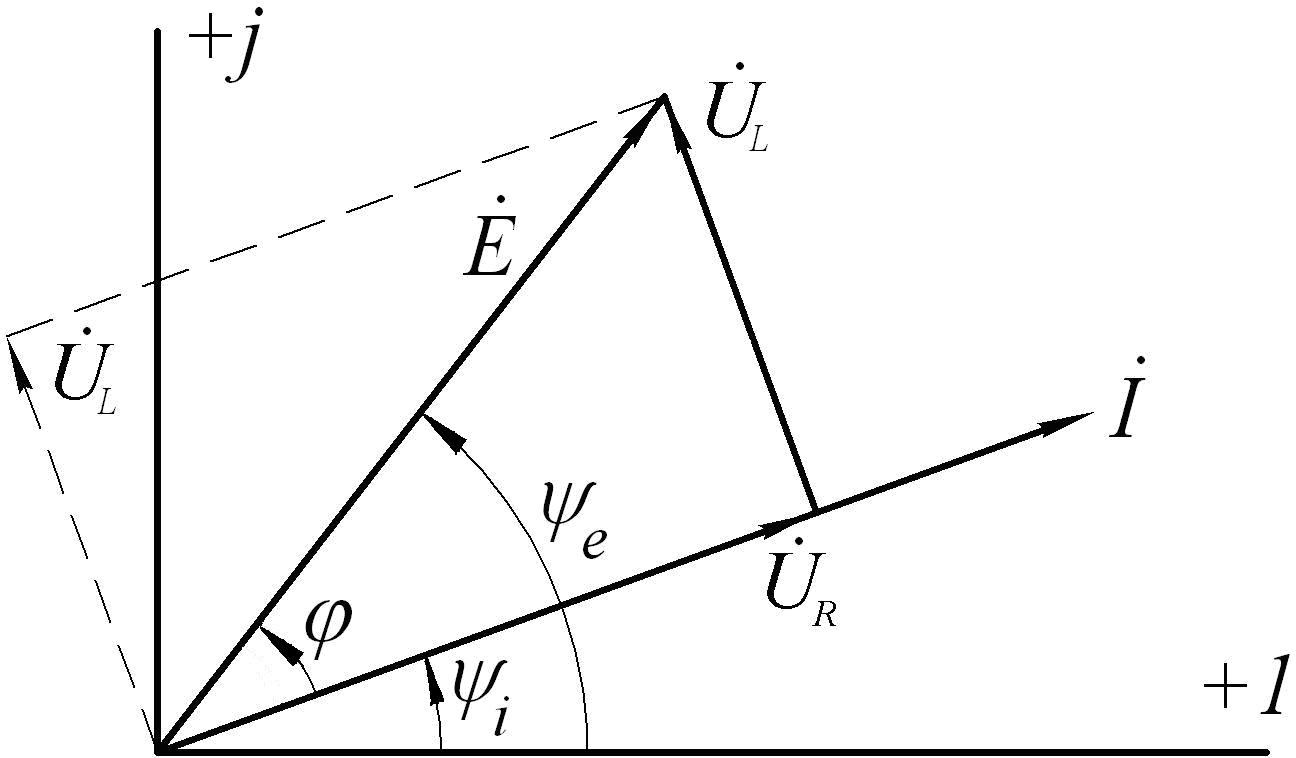 Итак, если известен ток в цепи
Итак, если известен ток в цепи