Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 389
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Отключение цепи RL от источника постоянного напряжения
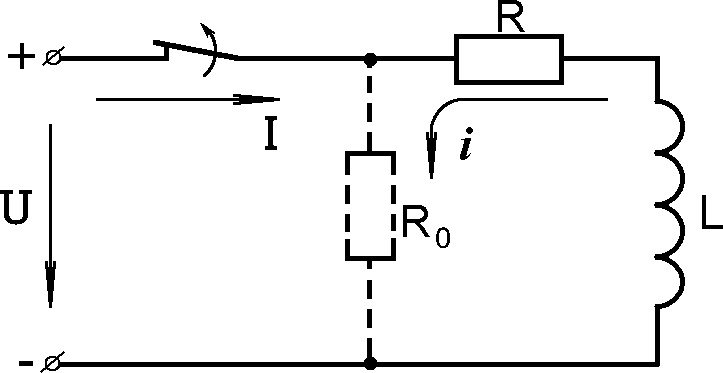
Рис.8.5
При отключении цепи, содержащей катушку индуктивности (рис.8.5), возникает ЭДС самоиндукции, препятствующая мгновенному прекращению тока.
В момент разрыва между контактами выключателя возникает дуга, поддерживаемая энергией магнитного поля катушки.
Скорость затухания тока определяют переходное сопротивление контактов и дуги.
Если индуктивность L велика, а ток уменьшается быстро, то ЭДС
самоиндукции
e Ldi
Ldt
может во много раз превышать приложенное к цепи
напряжение U. Такое перенапряжение опасно (возможен пробой изоляции).
Если в момент размыкания параллельно ветви RL включить сопротивление
R0 , то перенапряжение уменьшается, т.к. энергия WM
L I2
2
постепенно в виде тепла
будет выделяться в этом сопротивлении. В результате процесс спадания тока окажется более продолжительным, а ЭДС самоиндукции меньше. На практике используют различные дугогасительные устройства.
-
Включение цепи RL на синусоидальное напряжение
При включении цепи RL (рис.8.1) на синусоидальное напряжение
u Umsin(ω tψ)
в цепи устанавливается ток
iпр
Um
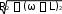 z
z sin(ω tψ
φ),
где z
, φ arctgω L.
R
Для свободной составляющей уравнение имеет вид:
Его решение
Ldiсв
dt
-
R iсв
-
Rt
0 .
-
t
где τ
L.
R
iсв
A eL
A eτ,
t0
Постоянная интегрирования определяется из первого закона коммутации
i|t0 iсв|t0 iпр|t0 0 . Отсюда следует, что
iсв iпр, а с другой стороны–
iсв
|t0
A ep0 A. Тогда,
A iпр
Umsin(ψ φ)
z
(t = 0, поэтому отсутствует
U t
компонента ω t). Следовательно,
iсв
A ept msin(ψ φ) eτ.
z
 Поскольку общий ток
Поскольку общий ток
i iсв iпр, то
i Umsin(ψ
z
φ) e
RtL
-
Umsin(ω t ψ φ
z
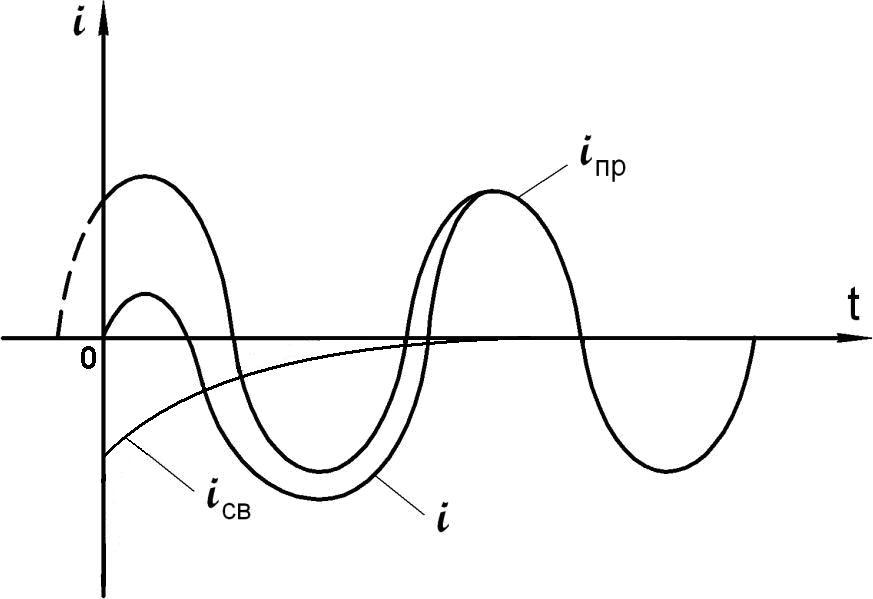
Графики свободного, принужденного и переходного токов в общем случае изображены на рис.8.6.
Если включение происходит в момент,
когда ток
iпр
проходит через нуль, то
свободный ток
iсв
не возникает и в цепи
Рис.8.6
сразу наступает установившийся режим.
Если включение произошло в момент, когда ток
iпр max
(рис.8.7), т.е.
ω tψ φ 90 , (ω t|
t0
0 ), то через половину периода (при
t T) общий ток i
2
достигает максимума, который при больших почти в 2 раза больше тока в установившемся режиме.
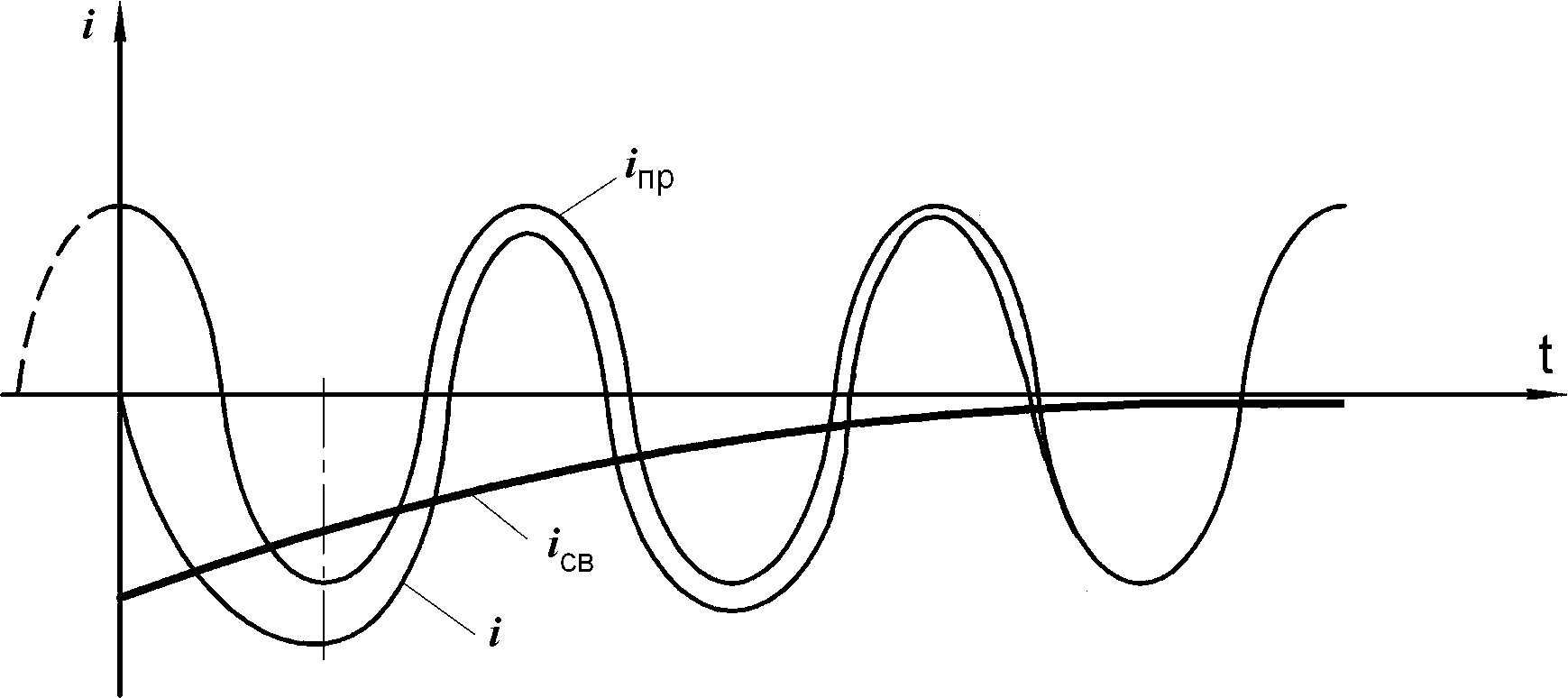
Рис.8.7
При расчете цепей (устройств) этот факт нужно учитывать, например, при расчете электродвигателя.
Переходные процессы в цепях с емкостью
-
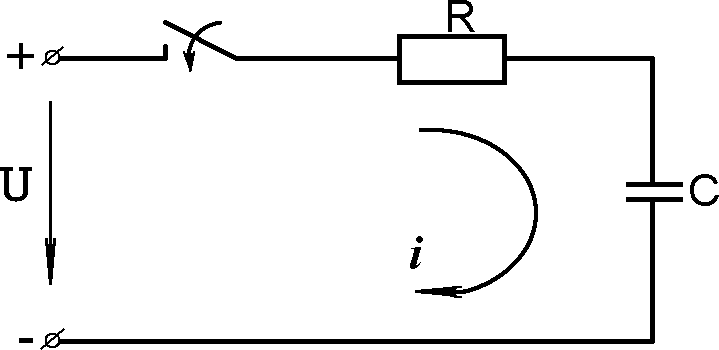
Включение цепи RC на постоянное напряжение
R
C
Для цепи (рис.8.8) уравнение по второму закону Кирхгофа имеет вид:
R
R
C
u u
U 0 , или u u
U.
Зная, что
u i R
получим:
Рис.8.8
C RduC
dt
-
uC
U, т.к. i CduC.
dt
Пусть получим:
uC uCпр uC св. Подставив данное выражение в предыдущее уравнение,
R C
d(u dt
Cпр
-
uCсв
) u
Cпр
-
uCсв
U.
Очевидно, что
uCпр|t U, т.к. за время
t
емкость полностью зарядится
до входного напряжения.
Подставим это значение в последнее уравнение и учтем, что получим:
duCпр
dt
0 ,
R CduCсв
dt
-
uCсв
0 . (8.7)
Cсв
Решением данного уравнения является выражение u A ept.
Постоянную интегрирования A найдем из второго закона коммутации:
(uCпр uCсв ) |t0 0 .
Отсюда
uCсв|t0 uCпр U. С другой стороны
u| A ep0 A.
Cсвt0
Тогда A U.
Величина корня pопределяется из характеристического уравнения, записываемого по виду уравнения (8.7)
R C p 1 0 .
Отсюда следует, что
p
1 .
R C
Тогда свободная составляющая напряжения на емкости будет равна
где τ
1
p
R C.
uCсв
U e
-
tRC-
t
-
U eτ, (8.8)
Окончательно, напряжение на емкости в процессе заряда равно
uC u
Cпр
-
uCсв
U U e
-
tRC-
t
-
U (1 eτ) .
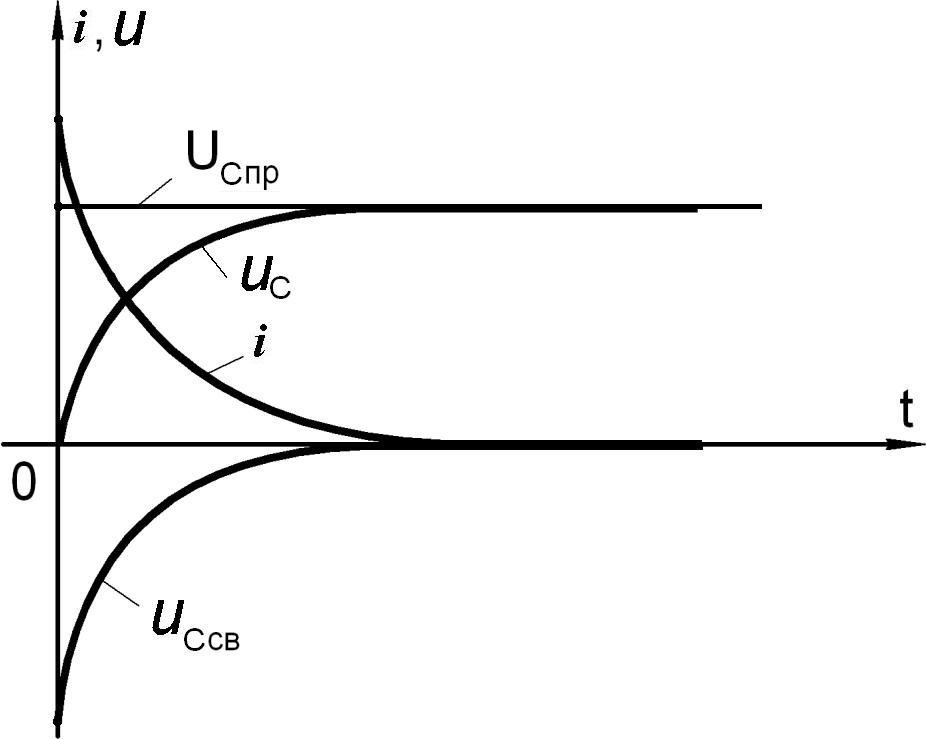 Воспользовавшись этим уравнением можно определить ток i:
Воспользовавшись этим уравнением можно определить ток i: