Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 413
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
совместного решения системы уравнений (8.19), но для
p2 δ j ωсв.
p1 δ j ωсви
В результате получим A
E U
A.
св
1 2 j ω L 2
Подставим
p1 , p2 A1
и A2
в (8.13), получим
i E U
2 jωсв L
e(δ jωсв)t
E U
2 jωсв L
e(δ jωсв)t
E U eδt ejω
t e jω
t
2 jωсв L
свсв
e
EU δt ejωсвt e jωсвt
EUsin ω
δt
ω L
2 j
ω L
свt e
свсв
При преобразовании была использована формула
ejZ
e jZ
2 j
sin Z.
Временная диаграмма колебательного процесса представляет собой экспоненциально затухающую синусоиду (рис.8.18).
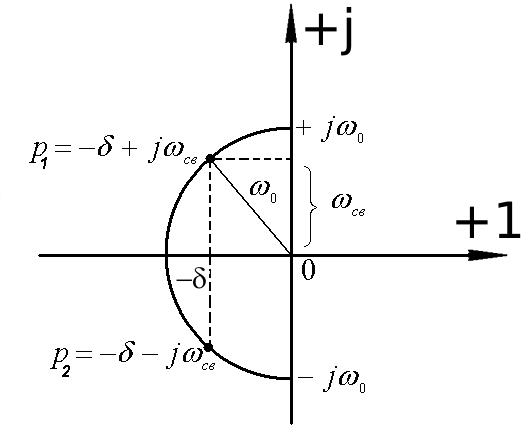
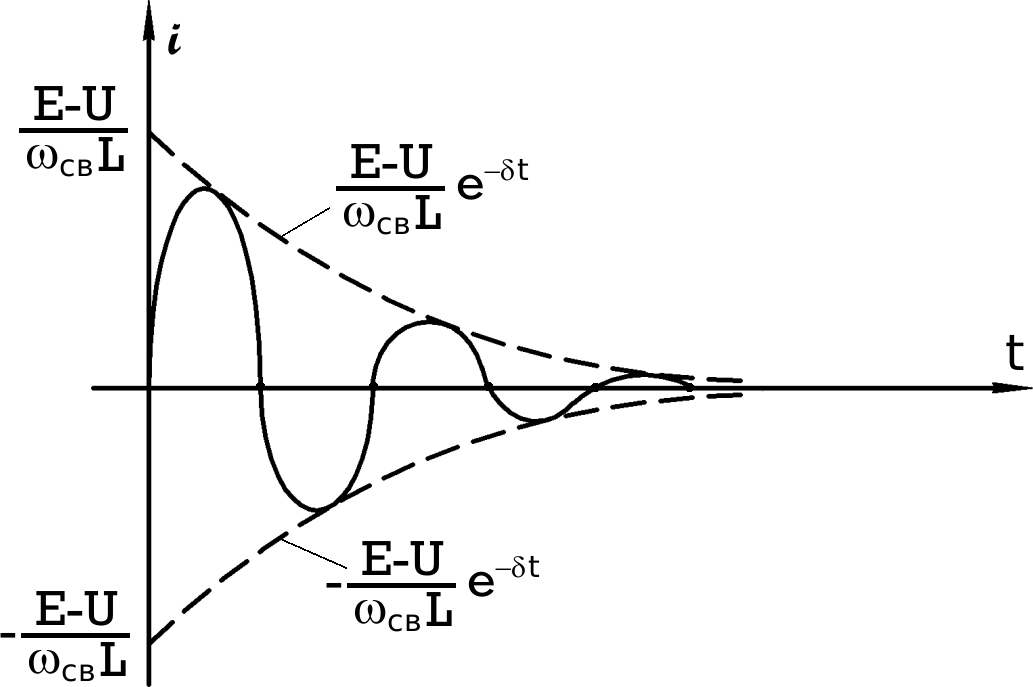 Рис.8.17 Рис.8.18
Рис.8.17 Рис.8.18- 1 ... 48 49 50 51 52 53 54 55 56
МАГНИТНЫЕ ЦЕПИ
-
Основные понятия
Часть электротехнического устройства, предназначенного для создания в его рабочем объеме магнитного поля заданной интенсивности, называется магнитной цепью.
Магнитная цепь состоит из элементов, возбуждающих магнитное поле (катушек с током, постоянных магнитов) и магнитопровода. Магнитопровод содержит ряд тел и сред, образующих замкнутые пути для основной части магнитных линий созданного поля.
Магнитные цепи подобно электрическим подразделяются на группы. Они могут быть с одним или несколькими элементами, возбуждающими магнитное поле, разветвленными и неразветвленными, с постоянными и переменными токами и т.п.
Основной величиной, характеризующей интенсивность и направление
магнитного поля в любой его точке, является вектор магнитной индукции B. Вектор
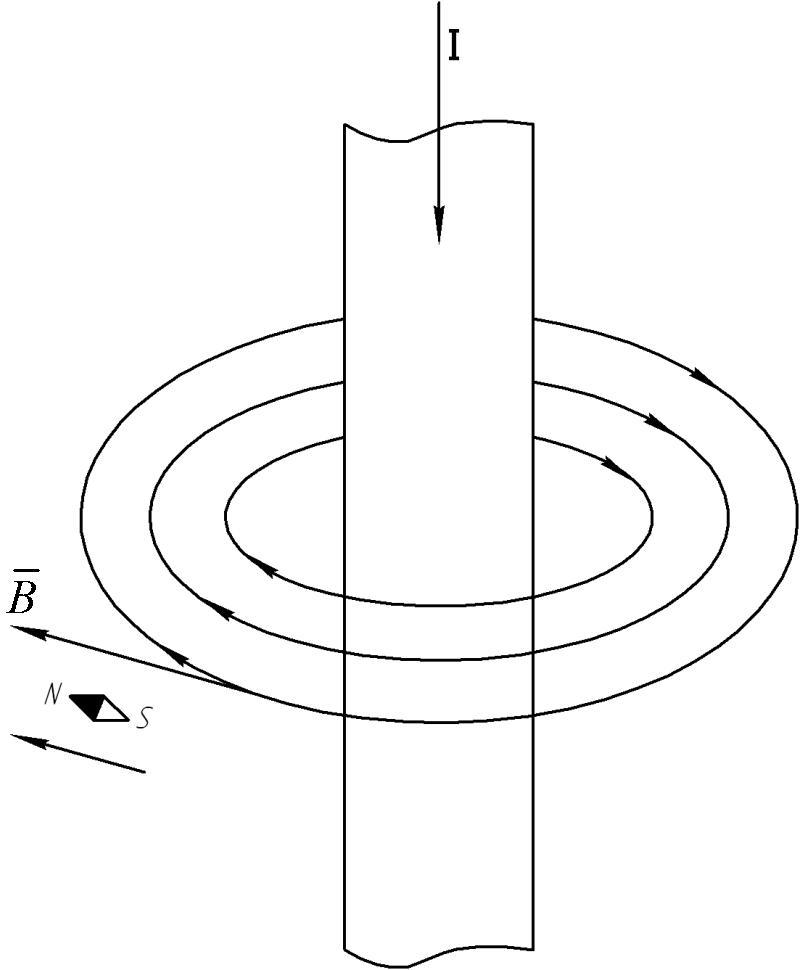
 Bнаправлен по касательной к силовой магнитной линии (рис.9.1).
Bнаправлен по касательной к силовой магнитной линии (рис.9.1).Рис.9.1 Рис.9.2
Направление вектора Bсовпадает с направлением магнитной стрелки,
помещенной в рассматриваемую точку поля и определяется по правилу правоходового винта (буравчика). Измеряется в теслах, Тл.
Второй важной величиной, характеризующий магнитное поле, является магнитный поток Ф, характеризующий густоту силовых линий поля.
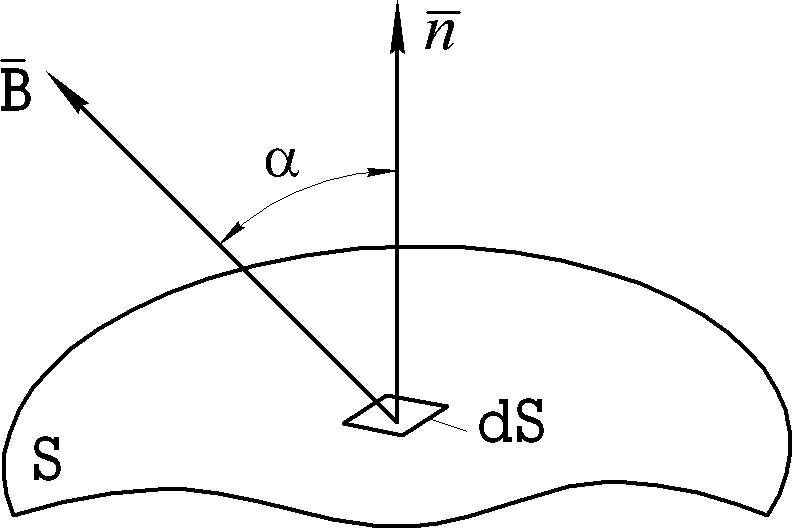
Элементарным магнитным потоком сквозь бесконечно малую площадь называется скалярная величина
где α- угол между вектором B
dФ B cosα dS,
и нормалью nк площадке dS(рис.9.2).
Поток через всю поверхность Sравен
Ф dФ B cosα dS.
SS
Если S– плоскость, то Ф B S cosα.
Если плоскость Sперпендикулярна к B, то рассчитывается по формуле
α 0 , а магнитный поток
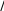 и измеряется в веберах, Вб.
и измеряется в веберах, Вб.Ф B S
(9.1)
Расчетной величиной является напряженность магнитного поля описывающая магнитное поле макротоков (токов проводимости).
Известно соотношение, связывающее Bи Н
Н, Aм–

0
a
B μ μ Н μH, (9.2)
где
μ 4 π107
Гнм
– магнитная постоянная; – магнитная проницаемость среды
0
(материала магнитопровода), показывающая, во сколько раз магнитное поле
a
макротоков усиливается за счет микротоков среды; μ– абсолютная магнитная
проницаемость среды. Для неферромагнитных материалов (медь, алюминий, воздух) практически не отличается от магнитной проницаемости вакуума. У
ферромагнитных материалов не является константой, а зависит от величины B. В основе расчета магнитных цепей лежит закон полного тока:

 Нdl Н cosα dl I,
Нdl Н cosα dl I,где Н– вектор напряженности магнитного поля в данной точке пространства; dl–
элемент длины замкнутого контура l; α– угол между направлениями векторов Ни
dl; I– алгебраическая сумма токов, пронизывающих контур l.
Ток
Ik, пронизывающий контур l, считается положительным, если его
направление и направление обхода контура связаны правилом правоходного винта (рис.9.3).
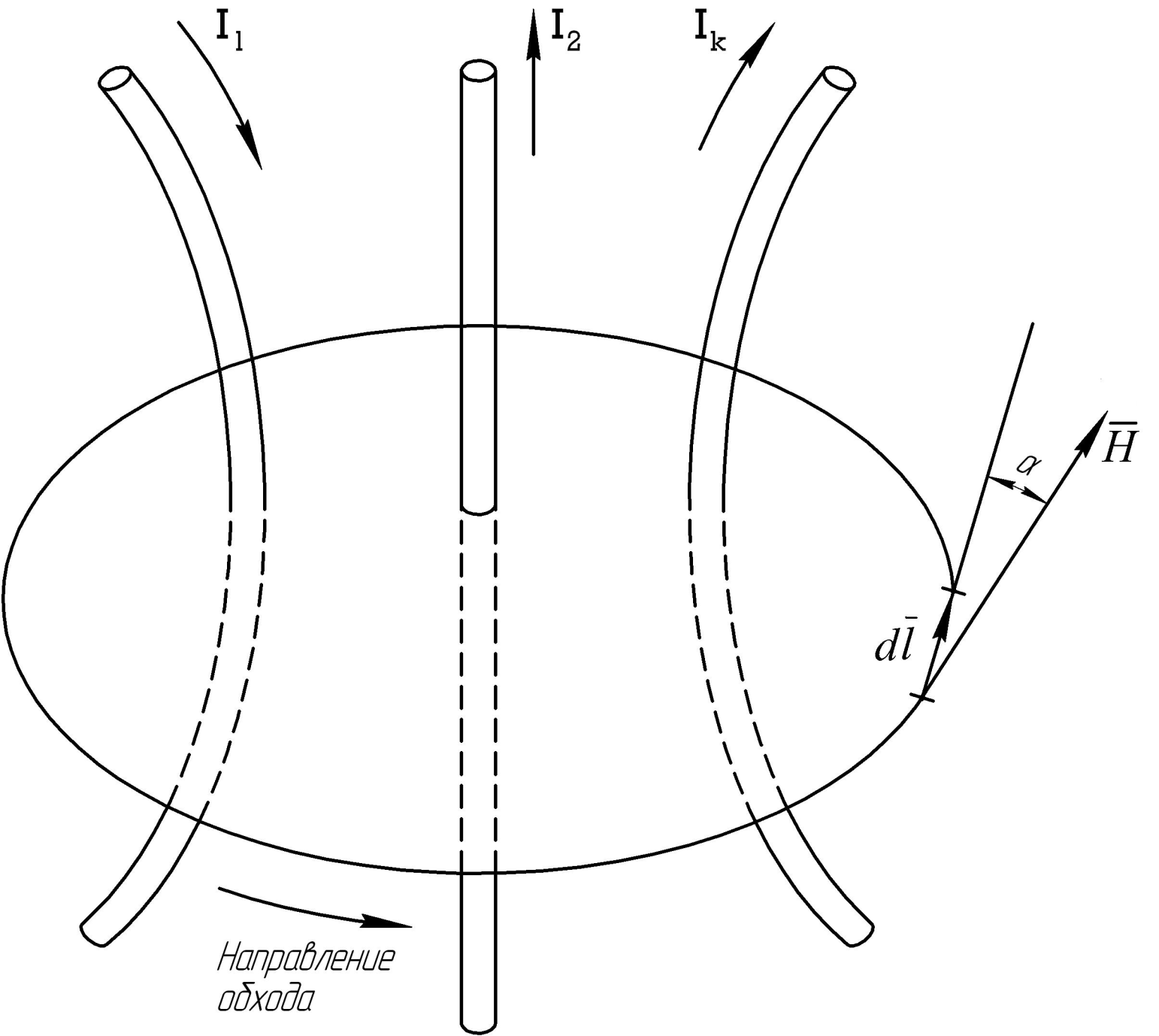
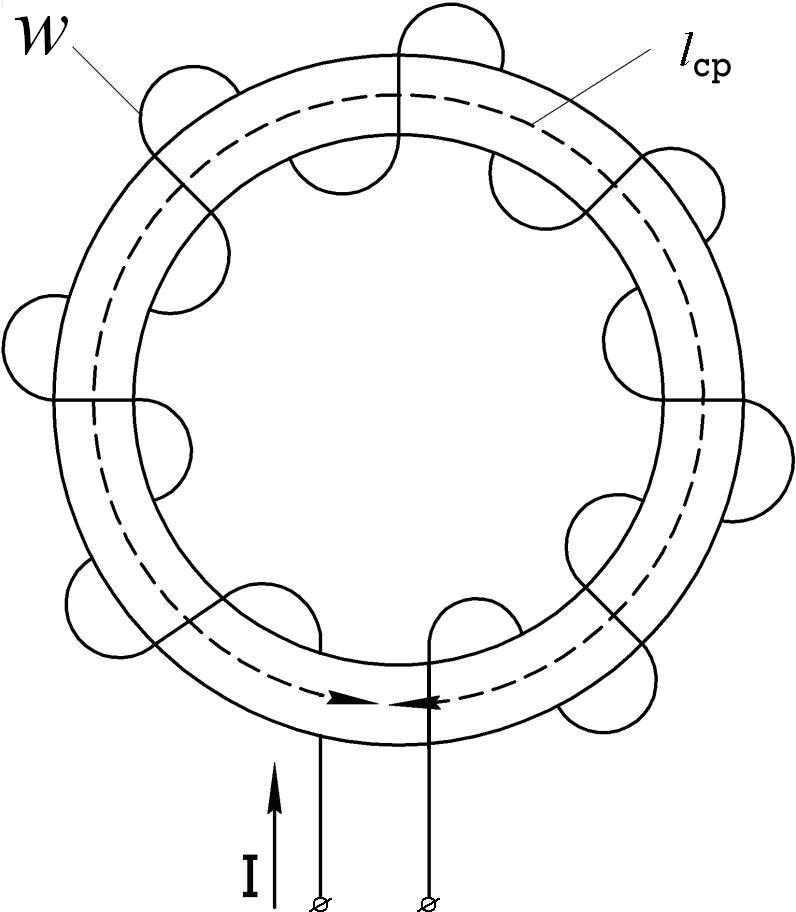
Рис.9.3 Рис.9.4
Для кольцевого магнитопровода (рис.9.4) закон полного тока запишется в
виде
Íñð lñð I w, т.к. угол
α 0
(векторы Hи dl
совпадают), величина
напряженности на средней линии
Нср
во всех точках контура из-за симметрии
устройства одинакова, а сумма токов, пронизывающих контур равна число витков обмотки.
Из этого выражения следует
I w, где w–
Н I w . (9.3)
срl
С учетом (9.1) и (9.2)
ср
Ф μа Н S. (9.4)
Подставим (9.3) в (9.4) получим закон Ома для магнитной цепи:
Ф μа
I w S
lср
I w lср
μа S
F. (9.5)
Rм
Здесь
F I w
- величина намагничивающей силы обмотки с током, а