Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 373
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
В рассмотренной выше цепи (рис 1.13) число соединительных элементов – три, следовательно, и число независимых контуров равно трем.
Число независимых контуров можно так же получить последовательным размыканием ветвей цепи до тех пор, пока не останется ни одного замкнутого контура, по которому может протекать ток. Общее число разомкнутых ветвей при этом и равно числу независимых контуров цепи.
-
ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ. РЕЖИМЫ РАБОТЫ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ. ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
-
Идеальные и реальные источники ЭДС и тока. Схемы замещения
Источники электрической энергии могут быть представлены схемой замещения с источником ЭДС или схемой замещения с источником тока.
Идеальный источник ЭДС –это активный элемент, напряжение на зажимахкоторого,независитоттока,идущеговнагрузку(рис.2.1). Внутреннее
сопротивление идеального источника ЭДС равно нулю r 0 .
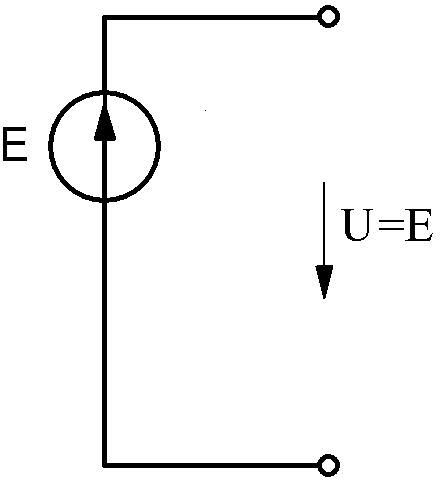
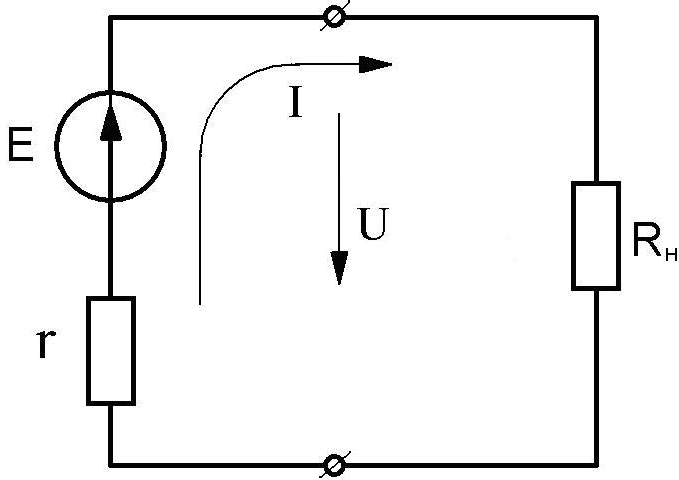
Рис.2.1 Рис.2.2
РеальныйисточникЭДС(рис.2.2) имеет внутреннее сопротивление
r 0 .
Обычно оно очень мало и составляет доли Ома. В соответствии со вторым законом
Кирхгофа U
E I r.
Чем больше внутреннее сопротивление r, тем сильнее напряжение на нагрузке отличается от ЭДС, т.е. чем больше r, тем хуже источник ЭДС.
Вольт-амперные характеристики идеального (1) и реального (2) источников ЭДС изображены на рис.2.3. Чем больше r, тем круче кривая (2). Идеальный источник ЭДС – источник бесконечной мощности.
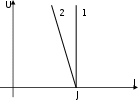
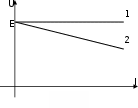 Рис.2.3 Рис.2.4
Рис.2.3 Рис.2.4Идеальныйисточниктока–этоактивныйэлемент,токкоторогоне зависитотнапряжениянаегозажимах(рис.2.5) иравентокукороткого
замыканияIкисточника. Внутреннее сопротивление идеального источника тока
r .
У реального источника тока (рис.2.6)
r , хотя и очень большое. В
соответствии с первым законом Кирхгофа
I J I J U.Чем меньше r, тем
нr
сильнее отличается ток в нагрузке хуже источник тока).
Iнот тока источника J( т.е. чем меньше rтем
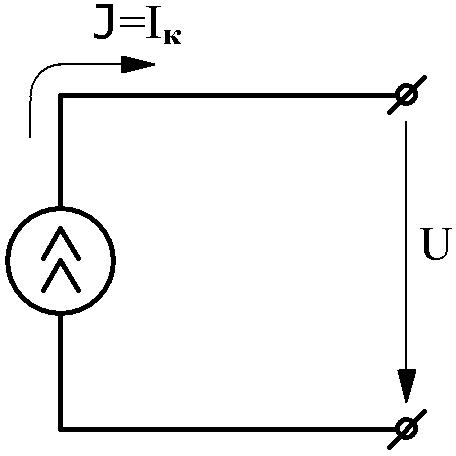
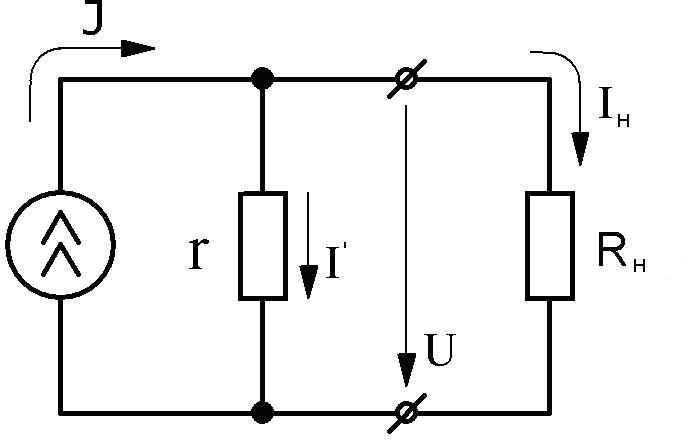
Рис.2.5 Рис.2.6
Вольт-амперные характеристики идеального (1) и реального (2) источников тока изображены на рис.2.4.
Чем меньше r, тем круче кривая.
Идеальный источник тока – источник бесконечной мощности.
Режимы работы электрической цепи
Различают четыре основных режима работы электрической цепи: номинальный, согласованный, режим холостого хода (хх) и режим короткого замыкания (кз).
Номинальный режим характерен тем, что напряжение, ток и мощность источника или приемника рассчитываются заранее на заводе – изготовителе. При этом обеспечиваются наилучшие условия эксплуатации электроустановки (экономичность, надежность).
Наиболее важным параметром является номинальное напряжение
Uном, т.к.
оно влияет на выбор электроизоляции и конструктивное исполнение элементов.
Номинальный ток электроустановки.
Iном
лимитируется предельной температурой нагрева
Номинальная мощность рассчитывается по формуле:
Pном Uном Iном.
Согласованный режим наступает при условии равенства сопротивления нагрузки и внутреннего сопротивления источника (генератора) r=Rн. При этом
источник отдает нагрузке максимальную мощность
Pmax
E2 .
4R
н
Режимы холостого хода (рис. 2.7) и короткого замыкания (рис.2.8) – предельные.
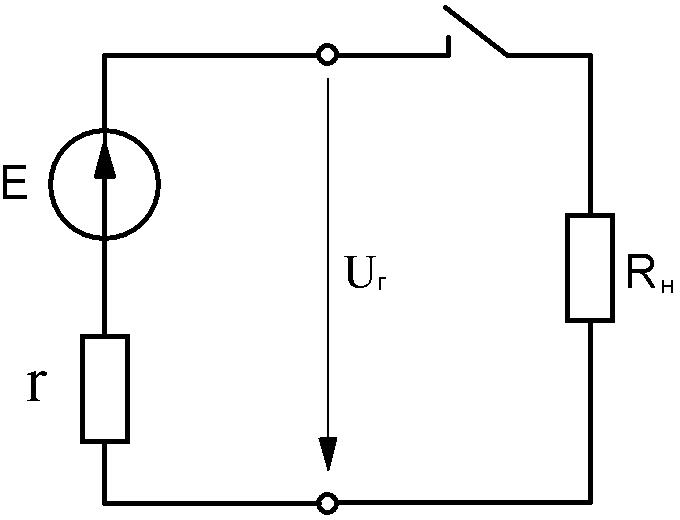
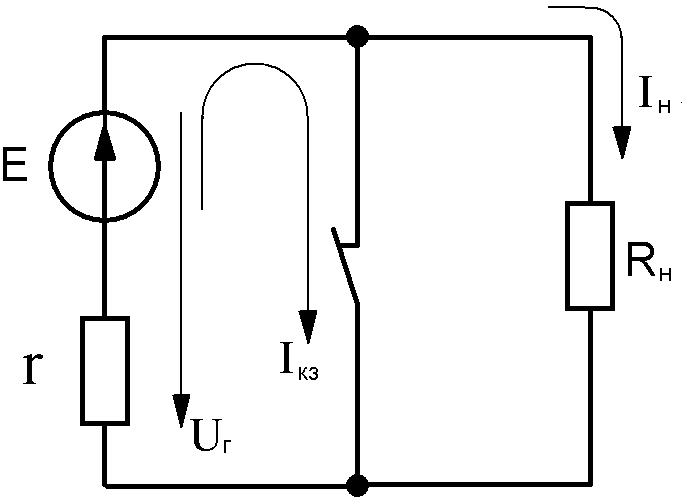
Рис.2.7 Рис. 2.8
В режиме холостого хода ключ разомкнут, поэтому является безопасным.
Iн 0 ,
Ur E; этот режим
Режим короткого замыкания – опасный. В опыте короткого замыкания ключ
E
замыкает между собой зажимы генератора. При этом ток в нагрузке
Iн 0 , Ur 0 . В
режиме эксплуатации ток короткого замыкания приводит электрооборудование к выходу из строя.
Iкз r
чрезвычайно велик и
-
Законы электрических цепей
-
Закон Ома для пассивного участка цепи
I U,
R
где I – сила тока, А; U – напряжение на участке цепи, В; R– сопротивление участка цепи, Ом.
-
Закон Ома для активного участка цепи
nm
φ1 φ2 Ei Ek
n
m
I i1 k1 ,
Rk
k1
ri
i1
где φ1 и φ2 – потенциалы на зажимах активного участка цепи (может быть задано
n
напряжение
U φ1 φ2 ); Ei– алгебраическая сумма источников ЭДС,
i1
совпадающих по направлению с током на участке цепи; Ek– алгебраическая
k1
сумма источников ЭДС, направленных навстречу току на участке цепи; Rk–
k1
n
алгебраическая сумма сопротивлений участка цепи; ri– алгебраическая сумма
i1
внутренних сопротивлений источников ЭДС.
-
Закон Ома для полной цепи
I E,
R r
где E– ЭДС на зажимах полной цепи; R– внешнее сопротивление цепи; r– внутреннее сопротивление источника ЭДС.
-
Первый закон Кирхгофа
n
n
Ikk1
0 ,
где Ik, k=1,2,…n – токи k– го узла (токи, направленные к узлу берутся со знаком
k1
минус, а от узла – со знаком плюс, или наоборот).
-
Второй закон Кирхгофа
n
n
Ik Rk
k1
m
Ek,
k1
где
Ik Rk– алгебраическая сумма падений напряжений на отдельных элементах
k1