Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 374

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56



C
индуктивная проводимость; проводимость данной цепи.

ω C b

– емкостная проводимость; Y– комплексная

Модуль полной проводимости данной цепи можно рассчитать по формуле
y  .

Угол между векторами общего тока и общего напряжения определяется по формуле:



Очевидно, что

1


φ arctgb arctgω L

g

ω C

.

g

  1. если

b 0

( b b

), то цепь будет носить индуктивный характер (см.

LC

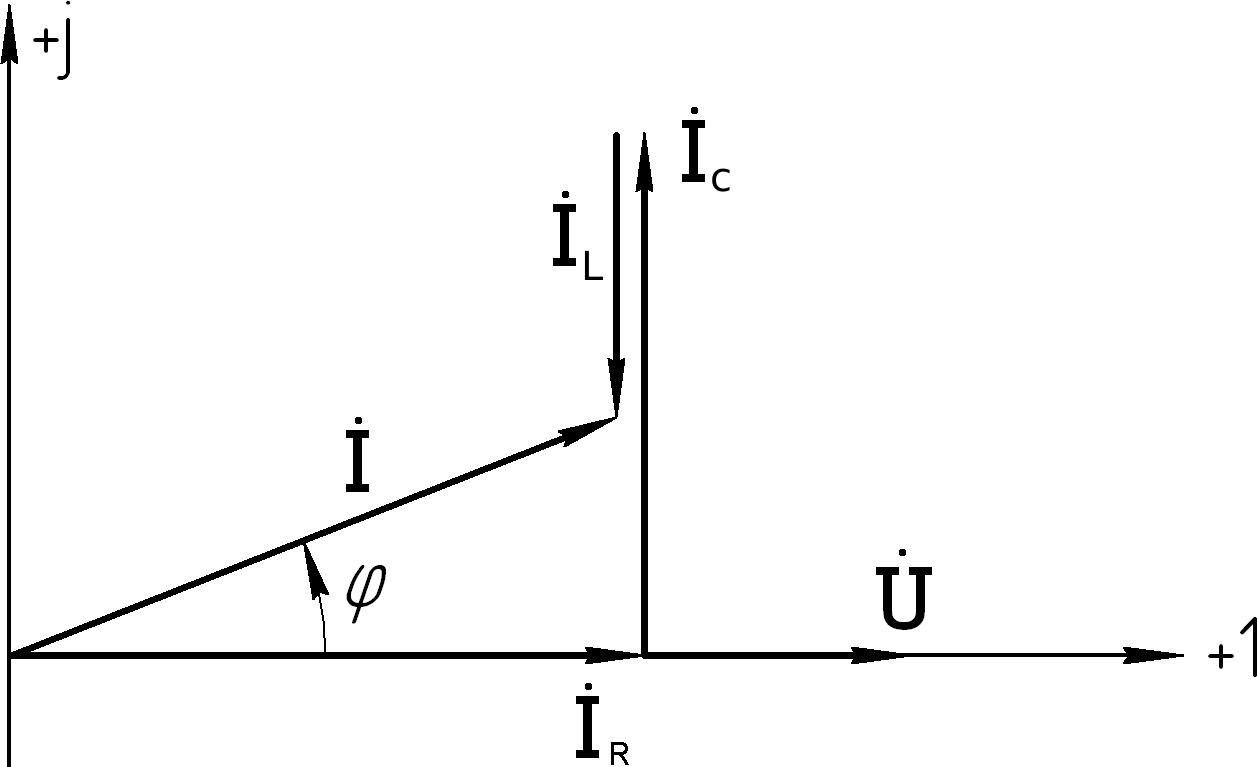векторную диаграмму на рис.5.36);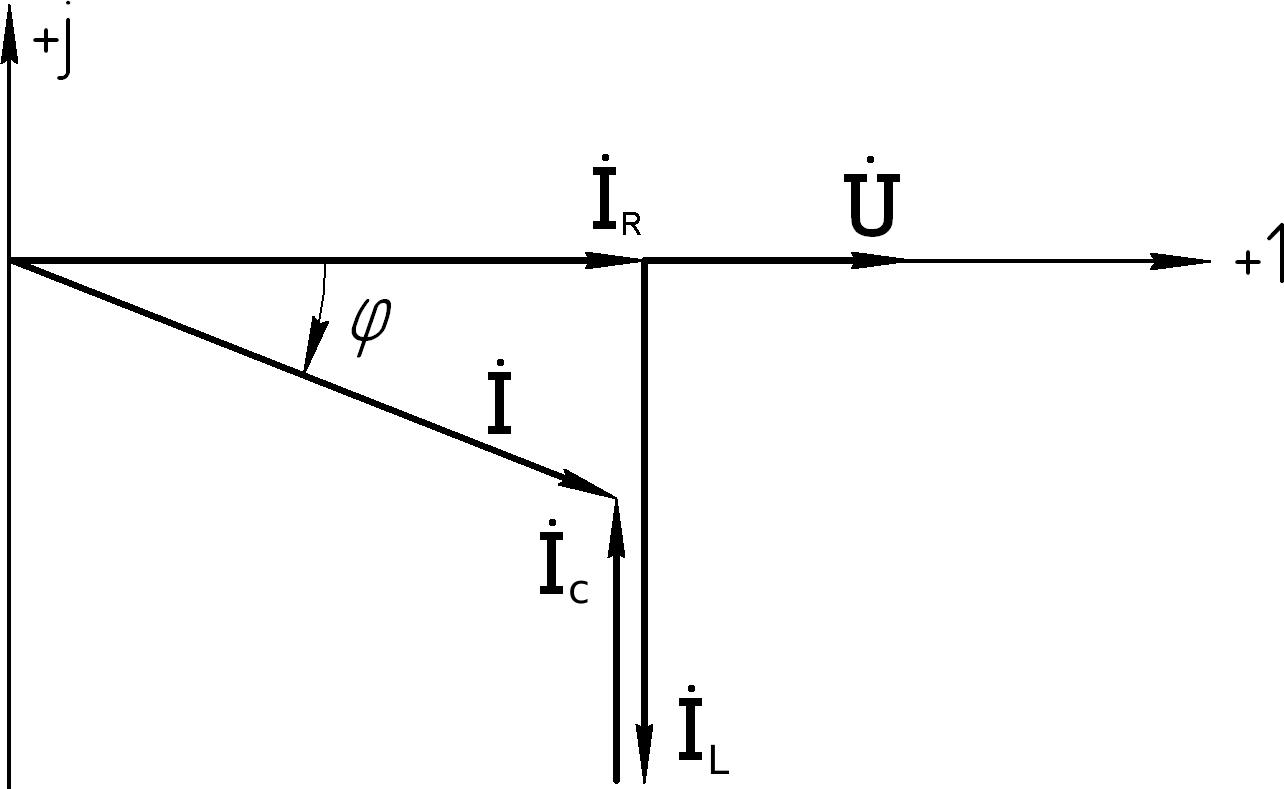



Рис.5.36 Рис.5.37

  1. если

b 0

( bL bC), то цепь будет носить емкостной характер (см. векторную

диаграмму на рис. 5.37);

  1. если

b 0

( b b), то цепь

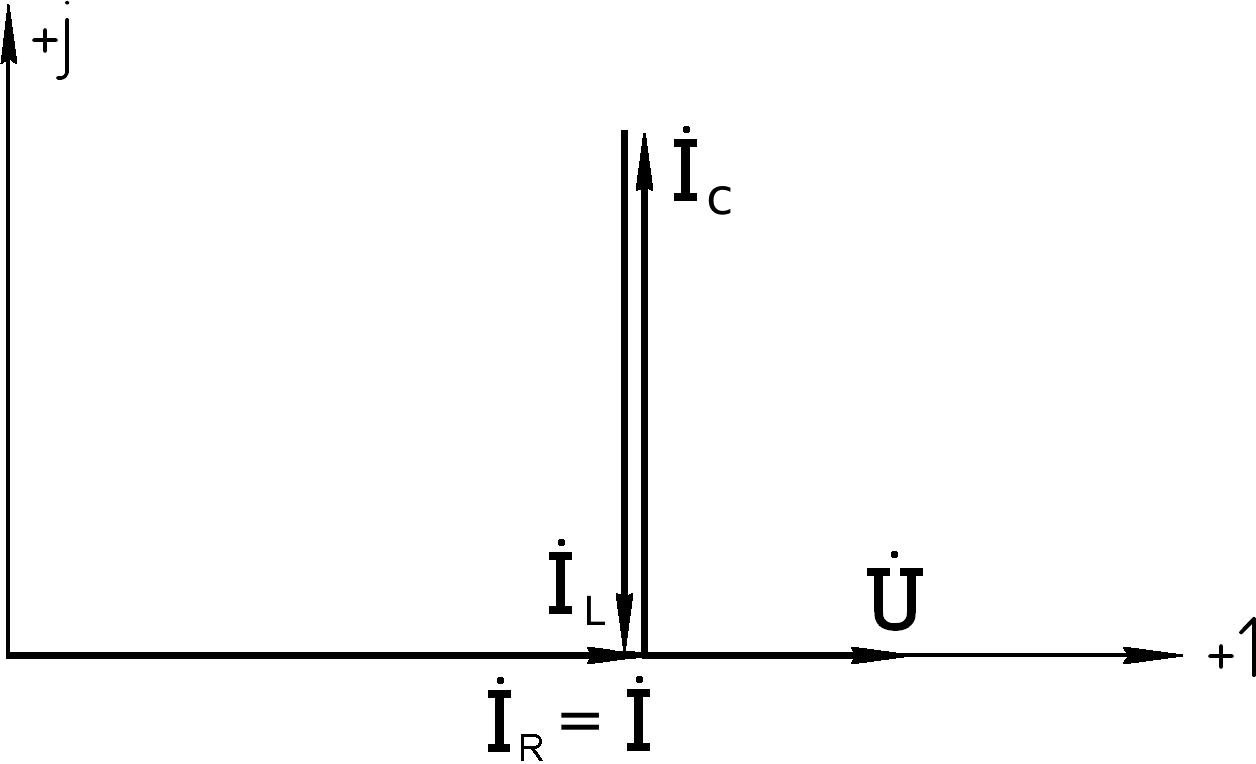LC

будет носить чисто активный характер (см. векторную диаграмму на рис.5.38).


Рис.5.38

Явление, при котором в параллельной цепи из R, L, С вектор общего напряжения совпадает по фазе с вектором общего тока, называется резонансом токов.


Таким образом, суммарный ток в неразветвленной части цепи равен току

через активное сопротивление, т.е.

I I .


R
В данном случае реактивная проводимость цепи равна нулю, а общая проводимость наименьшая, следовательно, и ток в неразветвленной части цепи I минимальный (в отличие от резонанса напряжений, когда ток был максимальным).

Здесь токи

I I

могут во много раз превосходить I . Поэтому это явление

LC

получило название резонанса токов.

Резонансная частота определяется из условия возникновения резонанса токов,

т.е. из условия

b b:


0
 LC

1


ω0 L

ω0
C ;

ω 1 .

Если при резонансе токов в одинаковое число раз n увеличить индуктивную и емкостную проводимости, т.е.


L
L0
C
C0
b nbи b nx,

то токи

I и

I увеличатся в nраз при неизменном значении общего тока в


L
C
неразветвленной части цепи

gU . Следовательно, можно получить любой по


0
I
величине ток в индуктивном и емкостном элементах при неизменном токе источника.

Резонанс токов для электроэнергетических установок явление безопасное, т.к. токи в обеих ветвях взаимно независимы и определяются приложенным напряжением (по закону Ома). Очевидно, что большие токи могут возникать только при малых значениях индуктивности L и больших значениях емкости C при заданном напряжении питания.

Явление резонанса токов широко используется на практике. Так, например, в резонансном усилителе параллельный контур с большой добротностью используется в качестве нагрузки, включаемой в коллекторную цепь транзистора усилительного каскада (для колебаний резонансной частоты его сопротивление велико, а, следовательно, велико и снимаемое с него напряжение, тогда как для остальных частот его сопротивление мало).

То свойство, что токи в ветвях в параллельном контуре много больше силы тока в неразветвленной части цепи, используется при устройстве индукционных печей, где нагревание металлов осуществляется вихревыми токами.


L
C
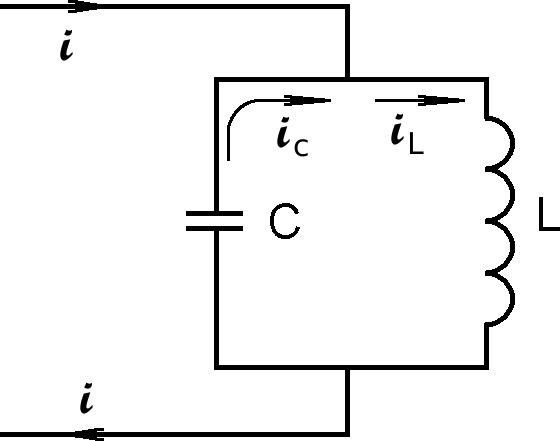
Параллельно нагревающей катушке L (рис.5.39) присоединяется конденсатор C с такой емкостью, при которой на частоте питающего генератора в данном контуре наблюдается резонанс токов.

Очевидно, что ток

i i i


Рис.5.39

намного меньше разогревающего тока

iL.


1   ...   26   27   28   29   30   31   32   33   ...   56

Треугольник проводимостей


Прямоугольный треугольник с катетами

I и ( I I

) и гипотенузой I

RLC

называется треугольником тока (см. векторные диаграммы, приведенные выше).

Если все стороны этого треугольника разделить на вектор U , то получим треугольник проводимостей, который служит геометрической интерпретацией выражения:

Y g

j 1 ω C .

ωL

Векторные диаграммы треугольника проводимостей для приведены на рис.5.40 и рис.5.41 соответственно.

b 0

и b 0


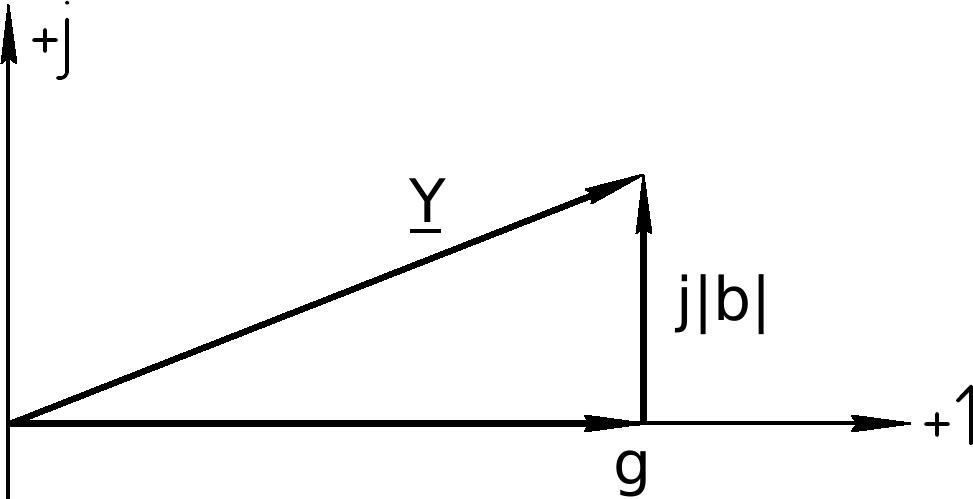
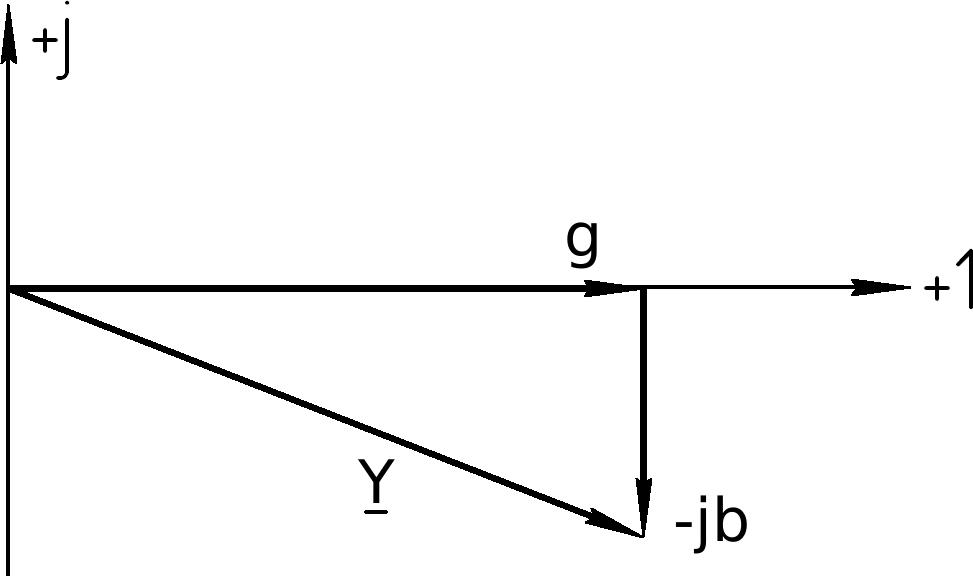Рис.5.40 Рис.5.41

      1. Эквивалентные преобразования схем электрической цепи


        1. Последовательное, параллельное и смешанное соединения Последовательное соединение.

В общем случае пусть имеем цепь вида (рис.5.42)




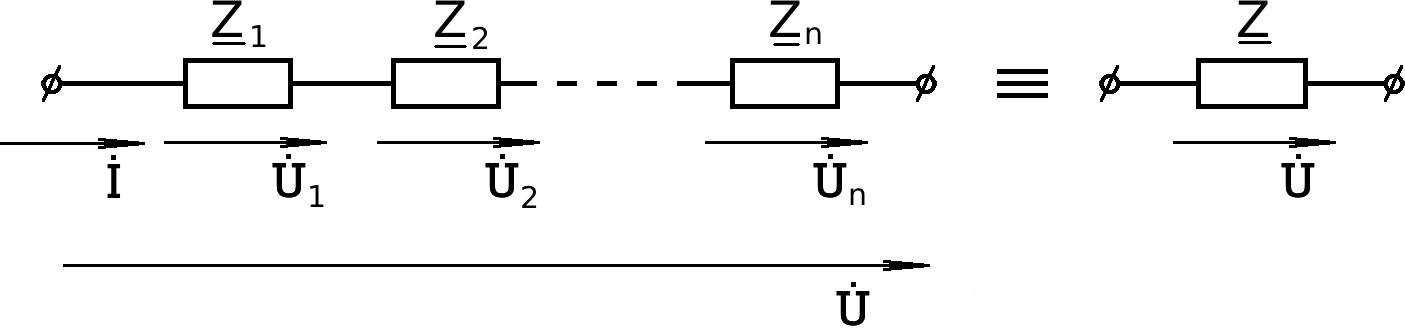
Рис.5.42

nn

Очевидно, что

Z Zk;

k1

U U1 U 2 U n U k.

k1

Сумма комплексных сопротивлений всех последовательно соединенных

n

участков цепи

сопротивлением.


Z Zkk1

называется эквивалентнымкомплексным

Рассмотрим два примера последовательного соединения элементов: RL (рис.5.43) и RC (рис.5.44).
1)





где

n




R Rk,

k1

n




L Lk.

k1

Рис.5.43


2)



Рис.5.44

где



R Rk,

k1

1 1 .


n

Ck1 Ck

Ток в таких цепях находится из выражения:

I U .

Z

1   ...   27   28   29   30   31   32   33   34   ...   56

Смотрите также файлы