Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

треугольником
Несвязанные трехфазные цепи не получили распространения на практике в силу своей неэкономичности, т.к. источник и приемник соединены друг с другом с помощью шестипроводной линии (рис.7.5).

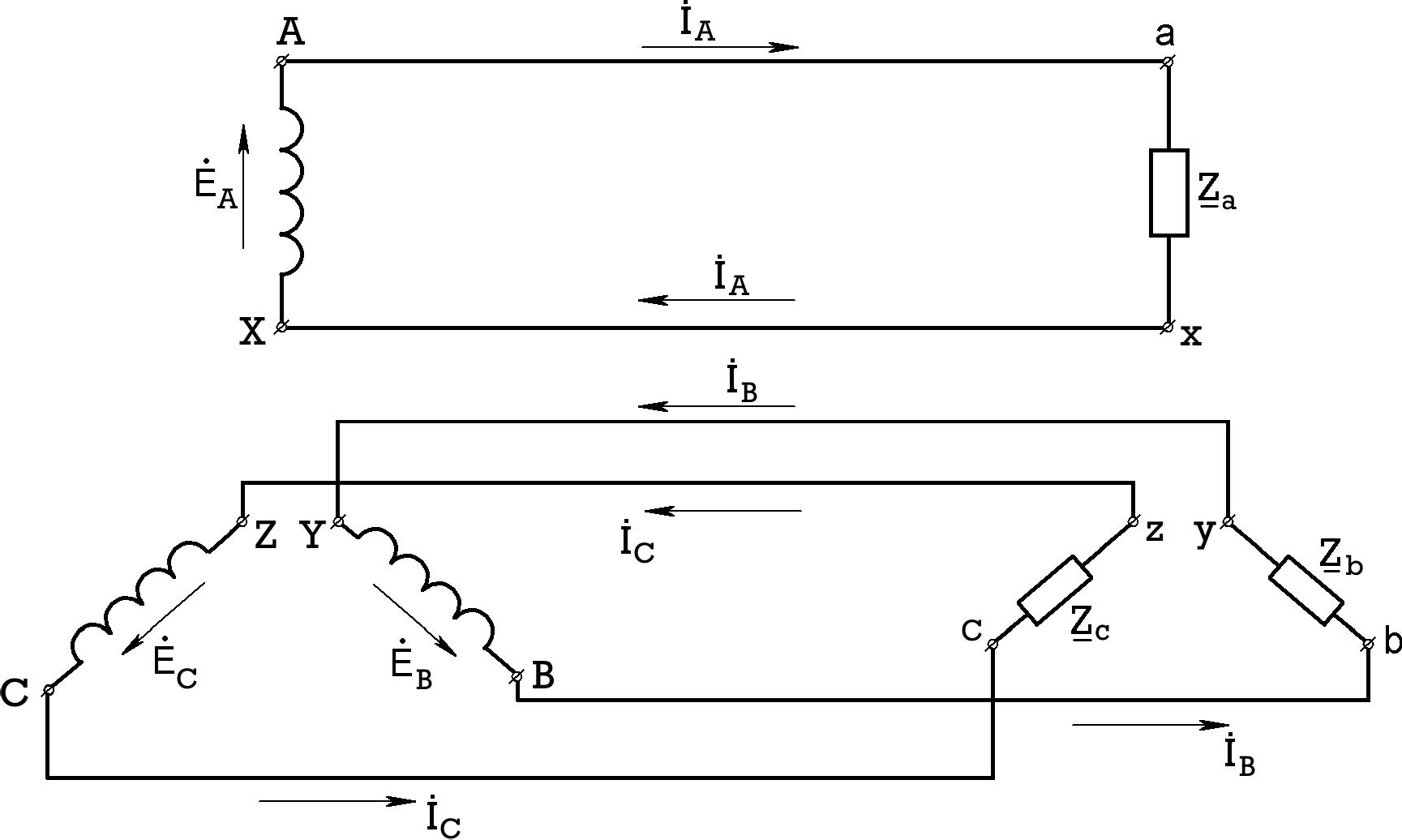
Рис.7.5
Рассмотрим соединение фаз трехфазного генератора звездой (рис. 7.6).

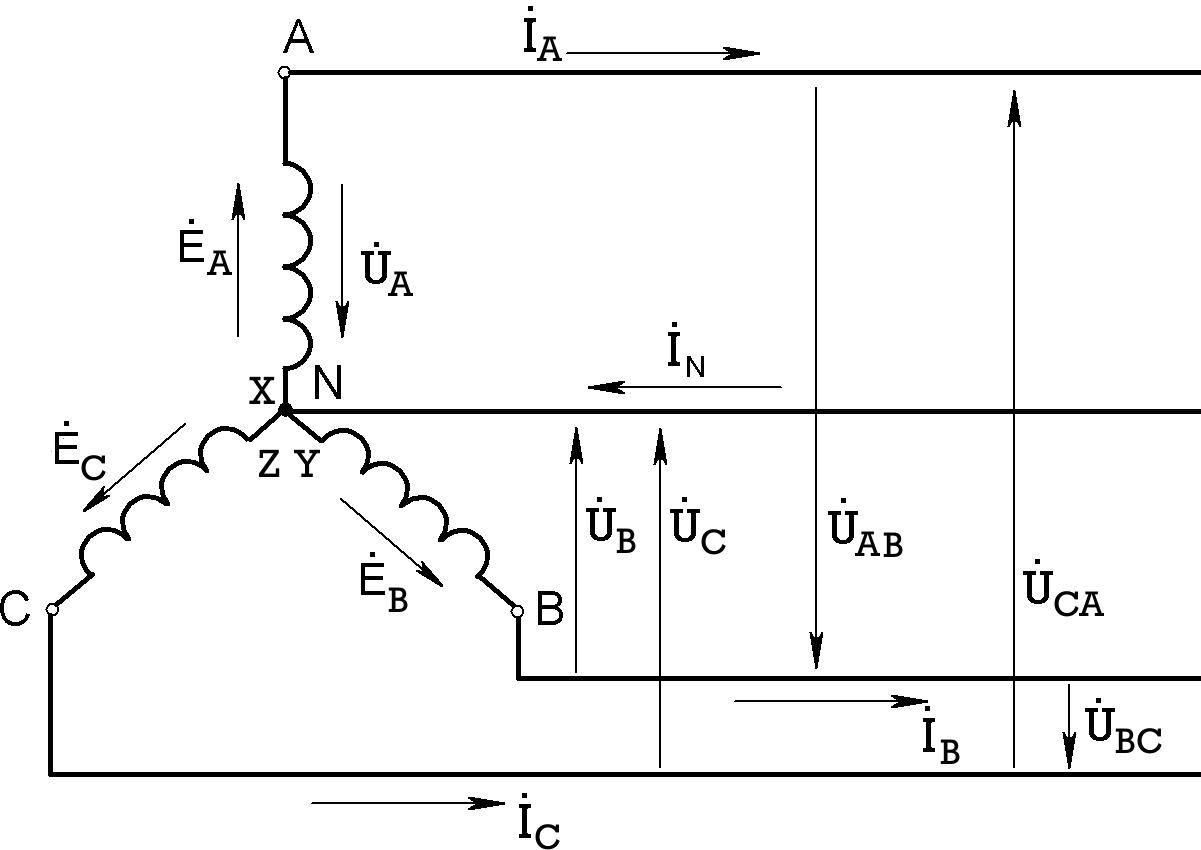
Рис.7.6

За условное положительное направление ЭДС в фазе принимают направление от конца к началу, а за положительное направление фазных напряжений – от начала к концу.

При соединении обмоток звездой, все концы обмоток соединяются в одну точку N, называемую нейтральной точкой. К началам обмоток A, B и C подключаются так называемые линейные провода, идущие к приемникам. Если нейтральные точки источника и приемника не соединены между собой, то трехфазная цепь называется трехпроводной. В противном случае трехфазная цепь называется четырехпроводной, а провод N-n, соединяющий нейтральные точки N источника и n приемника, называется нейтральным (нейтралью).

За положительное направление токов во всех линейных проводах, связывающих источник с нагрузкой, принимают направление от источника питания к нагрузке, а в нейтральном проводе – от приемника к источнику.

Напряжения

_U _, 

– называются

A

U

U

U,

и

B

C

AB
фазными, а напряжения ^

называются линейными.

 

U

и

U

–
BCCA

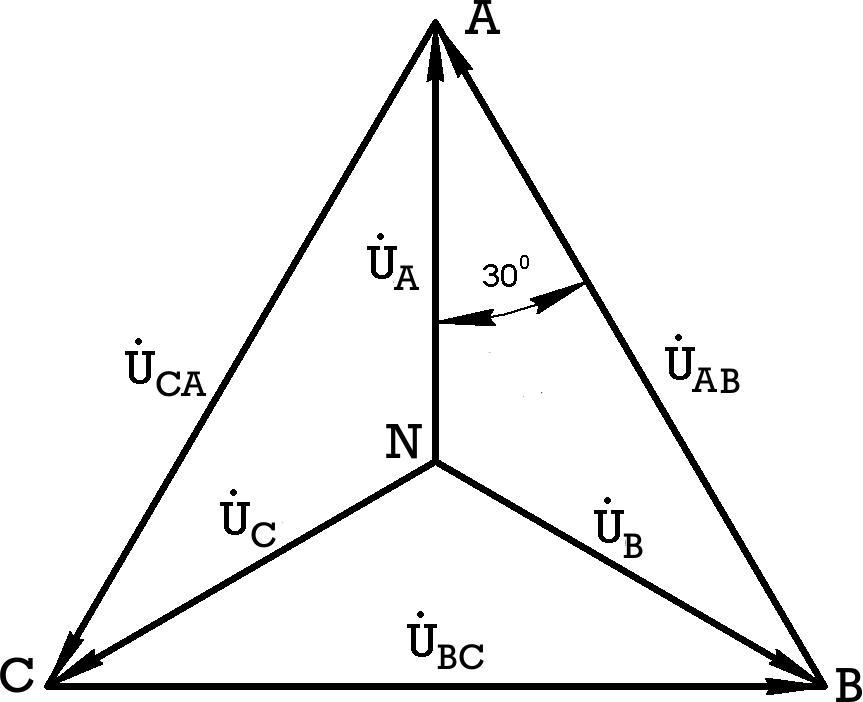
Векторная диаграмма для этого случая имеет вид, показанный на рис.8.7.

Из векторной диаграммы следует

U^_AB U^_A U^_B,

^U^BC

 U^_B U^_C,

U^_CA U^_C U^_A.

Рис.7.7

Важное свойство системы линейных напряжений: независимо от характера нагрузки сумма их мгновенных значений или векторов всегда равна нулю.

U,

U,

CA

AB

BC
Векторы линейного напряжения ^^U^опережают по фазе

соответствующие векторы фазных напряжений U^, U^, U^на угол

2 π

 30.

ABC ₆

Из векторной диаграммы легко получить численное соотношение между

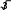
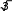линейными и фазными напряжениями (величина линейного напряжения в раз

больше величины фазного напряжения)

U_Л

U_Ф.

Линейный и фазные токи равны

I_Л I_Ф.

Номинальные напряжения для приемников низкого напряжения по ГОСТ:

U_Л 380 B U_Ф 220 B; U_Л 220 B U_Ф 127 B.

Рассмотрим соединение фаз трехфазного генератора треугольником.

При соединении треугольником в одну точку соединяются соответствующие начала и концы фаз (рис.7.8) X-B, Y-C, Z-A.

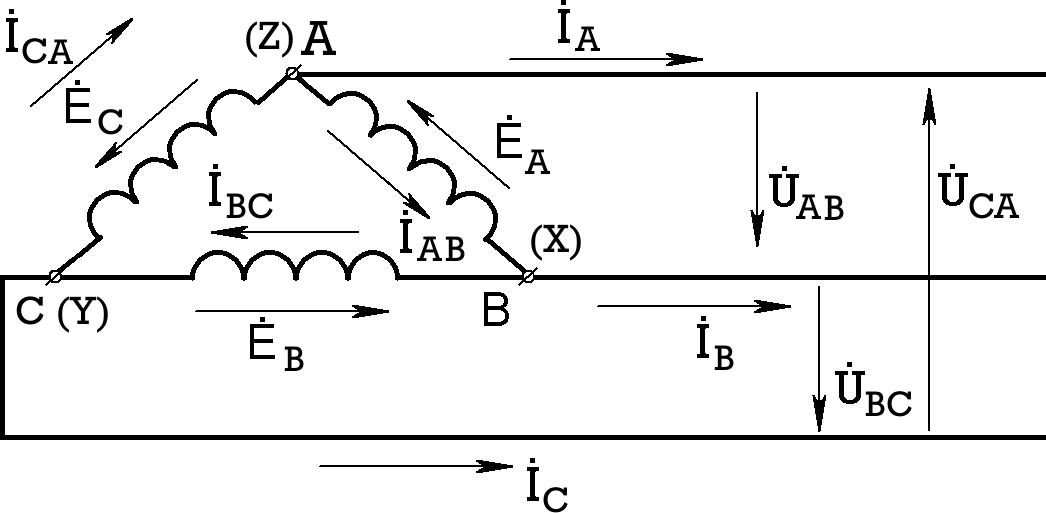
Рис.7.8

Л

Ф
Из данной схемы следует, что при соединении фаз источника треугольником,

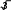
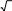линейные напряжения равны фазным

U U

, а линейные токи в данном случае

больше фазных в

раз, т.е. I_Л

 3  I_Ф(см. рис.7.13).

Такое соединение фаз генератора не равносильно их короткому замыканию (как это имело бы место при подобном соединении фаз источников синусоидального тока), т.к. если фазы симметричны (содержат одинаковое число витков) сумма мгновенных значений фазных ЭДС или изображающих их векторов

всегда равна нулю, т.е.

E^ E^

 E^

 0 . Поэтому при холостом ходе никакого тока

AB

C
в фазах источника нет. Однако даже незначительное отклонение от симметрии вызовет уравнительный ток в обмотках источника. В связи с этим на практике обмотки генератора стараются соединять звездой.

1 ... 34 35 36 37 38 39 40 41 ... 56

Трехфазные цепи с симметричными пассивными приемниками

Соединение звездой (3-х и 4-х проводные цепи)

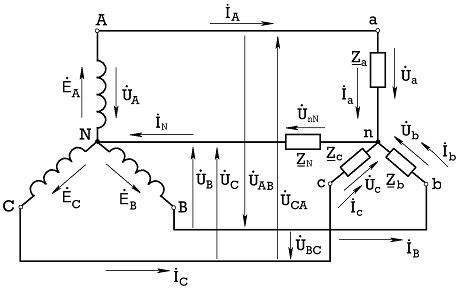
Рис.7.9
Условием симметричности нагрузки является равенство комплексных

сопротивлений фаз

Z_a Z_b Z_c.

Если считать, что линейные сопротивления проводов и нейтрали равны нулю, то фазные напряжения приемника равны фазным напряжениям источника:

aAbBc

C
U^ U^; U^ U^; U^ U^.

В этом случае фазные токи приемника, протекающие по фазам с

сопротивлениями

Z_a,

Z_b,

Z_cможно определить по формулам:

Z

a
I^ ^U^^a;

a

I^ ^U^^b;

Z

b
b

I^ ^U^^c,

Z

c
c

а ток в нейтрали

_I_N

 I^

 I^

 I^.

c

a

b
Можно видеть также, что

I^_A I^

; I^ I^;

I^ I^.

B

b

C

c

a
Итак, при симметричной нагрузке токи в фазах равны по величине и сдвинуты на один и тот же угол относительно соответствующих фазных напряжений (рис.7.10).

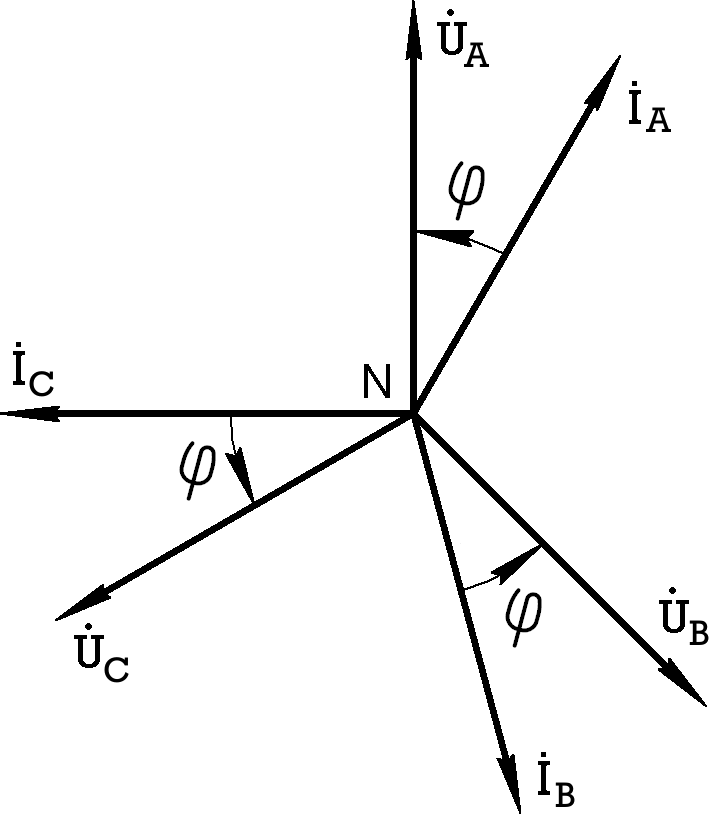
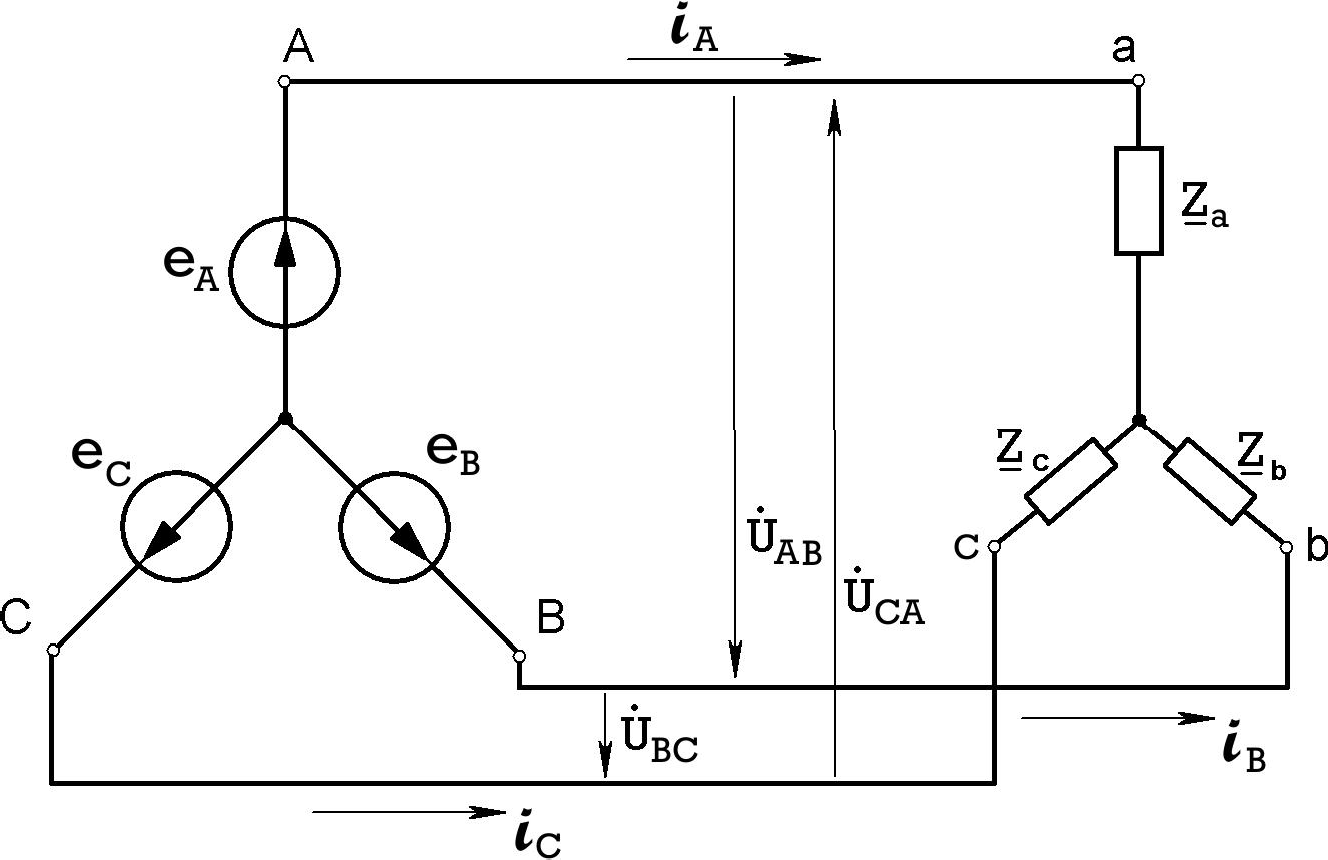
Рис.7.10
Отсюда следует, что
I^_A I^_B I^
Рис.7.11

C
 0 , т.е. при симметричной нагрузке ток в

нейтральном проводе отсутствует и, следовательно, отпадает в нем необходимость. Такая трехфазная цепь будет трехпроводной (рис.7.11).

Для определения токов в трехпроводной цепи при соединении приемников в звезду достаточно определить ток лишь в одной из фаз (остальные равны этому

значению)

I ^U^Ф

Z

Ф
Ф

. Линейные токи равны фазным

I_Ф I_Л

, а фазное напряжение в

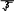раз меньше линейного U ^U^Л.
В трехпроводную цепь при соединении нагрузки звездой включают только симметричные трехфазные приемники – электродвигатели, печи, нагреватели для воды и т.д.

1 ... 35 36 37 38 39 40 41 42 ... 56

Смотрите также файлы

Дипломный проект на тему "Организация работы отделения по ремонту колесных пар пассажирского вагонного депо".docx

Жалпы білім беретін мектептердегі педагогдефектологты жаттары.docx

Фгбоу во тувинский государственный университет кызылский педагогический институт им. Народного писателя тувы а. А. Даржая.docx

Формирование морфологической стороны речи. Игры и упражнения с грамматическим содержанием для детей 34 лет.docx

Контрольная работа по дисциплине Инженерные изыскания при ведении кадастра.rtf

Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Смотрите также файлы

Информация

Списки файлов

Дополнительно