Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 387
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Соединение треугольником
Формулы для определения мощности в данном случае такие же, как и в предыдущем случае. Мощности отдельных фаз:
PAB UAB IAB cosφAB; PBC UBC IBC cosφBC ; PCA UCA ICA cosφCA ;
QAB UAB IABsin φABQBC UBC IBCsin φBCQCA UCA ICAsin φCA.
Общая мощность равна сумме мощностей отдельных фаз:
P PAB PBC PCA; Q QAB QBC QCA.
При симметричной нагрузке, когда мощности фаз равны:
P 3 PФ 3 UФ IФ cosφ;
Q 3 QФ 3 UФ IФ sinφ;
Ф
S 3 U I.
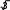 Ф
ФУчитывая, что при соединении треугольником
UЛ UФ
и IЛ
IФ, получим
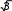 мощности, выраженные через величины линейного тока и линейного напряжения:
мощности, выраженные через величины линейного тока и линейного напряжения:P
UЛ IЛ
cosφ;
 Q
QUЛ IЛ
sinφ;
S
UЛ IЛ.
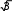 Таким образом, независимо от способа включения трехфазной нагрузки мощности рассчитываются по одинаковым формулам.
Таким образом, независимо от способа включения трехфазной нагрузки мощности рассчитываются по одинаковым формулам.- 1 ... 40 41 42 43 44 45 46 47 ... 56
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
8.1 Основные понятия
Процессы в цепи, возникающие при переходе от одного установившегося (стационарного) режима к другому, называются переходными.
В электрической цепи переходные процессы возникают при изменении режима ее работы: включении или отключении цепи, изменении параметров R, L или C. Такие действия, вызывающие переходные процессы, называются коммутацией.
Каждому состоянию цепи, имеющей индуктивность L и емкость C, соответствуют определенные запасы энергии магнитного и электрического поля:
L i2
W L;
M 2
C u2
W C.
Э 2
Для изменения энергии поля на конечную величину необходимо некоторое время, т.к. скачкообразное изменение энергии было бы равносильно тому, что
мощность источника достигала бы бесконечных значений ( P dW
dt
), что
физически невозможно.
В связи с этим – скачкообразные изменения тока iL
в катушке индуктивности
и напряжения uC
на конденсаторе невозможны. Следовательно, переход от одного
установившегося значения к другому совершается не мгновенно, а лишь за некоторое время (хотя и очень быстро – за доли секунды).
Первыйзаконкоммутации.
Ток в цепи с индуктивностью не может изменяться скачком и в начальный момент времени переходного процесса (t=0) сохраняет свое предшествующее значение.
Второйзаконкоммутации.
Напряжение на зажимах конденсатора не может изменяться скачком и в начальный момент времени переходного процесса (t=0) сохраняет свое предшествующее значение.
Математический анализ переходных процессов в электрических цепях базируется на том, что законы Кирхгофа применимы не только к установившимся, но и к неустановившимся режимам.
Используя первый и второй законы Кирхгофа можно получить линейные дифференциальные уравнения для переходного процесса. По этим уравнениям определяют значения токов и напряжений в любой момент рассматриваемого процесса. Значения постоянных интегрирования находят из граничных условий, определяемых законами коммутации.
Для упрощения решения дифференциальных уравнений и их анализа переходный процесс принято рассматривать как результат наложения двух режимов: принужденного и свободного. В соответствии с этим действительный ток
в цепи iпредставляется как сумма принужденного тока
iпр, который
устанавливается в цепи по окончании переходного процесса, и свободного тока протекающего в цепи только в течении переходного процесса
i iсв iпр.
iсв,
i
Свободный ток постепенно уменьшается и при установившемся режиме (t=∞)
становится равным нулю, т.е.
i|t
пр .
Оперируя в расчетах принужденной и свободной составляющими тока, необходимо помнить, что реально существуют не эти отдельные составляющие, а результирующие токи или напряжения.
Переходные процессы в цепях с индуктивностью
-
Включение RL цепи на постоянное напряжение
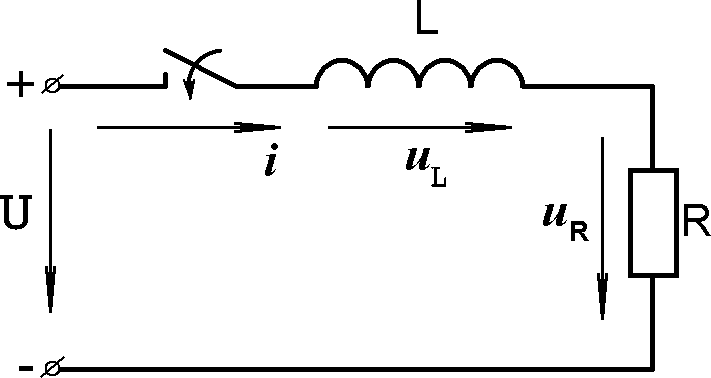 Запишем уравнение по второму закону Кирхгофа для данной цепи (рис.8.1):
Запишем уравнение по второму закону Кирхгофа для данной цепи (рис.8.1):L
R
u u U 0 ;
LR
U u u.
Или (раскрыв uLи uR)
Рис.8.1
U Ldi i R. (8.1)
dt
Пусть мгновенный переходный ток в цепи равен i iпр iсв. Стоит задача
нахождения составляющих тока iпри iсв. Подставив это выражение в уравнение (8.1), получим:
Ld(i
dtпр
-
iсв
) (iпр
-
iсв
) R U. (8.2)
Очевидно, что
iсв|t 0 , т.е. в установившемся режиме
iсв 0 . Тогда
уравнение (8.2) можно записать относительно принужденной составляющей тока
Ldiпр
dt
-
iпр
R U. (8.3)
Очевидно, что iпр|t const, следовательно:
Вычтем (8.3) из (8.2), получим
Ldiпр
dt
iпр
0 и
U. (8.4)
R