Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Одному обороту двухполюсного ротора соответствует один период переменной ЭДС. Если же ротор имеет pпар полюсов, то одному обороту ротора будет соответствовать pпериодов переменной ЭДС. Если ротор делает nоборотов

в минуту, то за минуту ЭДС генератора будет иметь

n p

периодов. Запишем

временное соотношение

60  n p T, отсюда

T ⁶⁰или

n p

f ¹

T

 ⁿ^^p. Эти

60

формулы будут использоваться при изучении дисциплины “Электрические машины”.

Изображение синусоидальных e , u , i в виде векторов

Известно несколько способов представления синусоидально изменяющихся величин: в виде тригонометрических функций (5.1), в виде графиков изменений во времени (волновых диаграмм) (рис.5.1), в виде вращающихся векторов (рис.5.3) на декартовой и комплексной плоскостях.

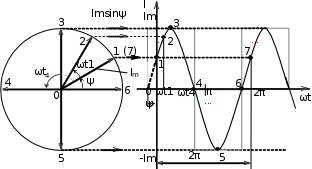
Рис.5.3
На рисунке 5.3 положениям 1, 2, 3, 4, 5, 6, 7 вращающегося вектора I_m

соответствуют точки 1, 2, 3, 4, 5, 6, 7 волновой диаграммы синусоидальной функции.

Векторное изображение синусоидальных величин (векторная и векторно– топографическая диаграммы), изменяющихся по гармоническому закону, позволяет с помощью вращающихся векторов, расположенных в одной плоскости, представить в наглядной форме значения электрических величин для различных участков электрической цепи и их относительное отставание или опережение по фазе.

Для того, чтобы изобразить эти функции в виде векторов на декартовой плоскости требуется из начала осей координат провести векторы, равные амплитудным значениям соответствующих величин, и придать им вращение против часовой стрелки с угловой скоростью, равной угловой частоте .

Фазовый угол всегда отсчитывается от положительной оси абсцисс: положительный угол откладывается от положительной оси против часовой стрелки, а отрицательный угол – по часовой стрелке; проекции вращающихся векторов на ось ординат равны мгновенным значениям соответствующих синусоидальных величин.

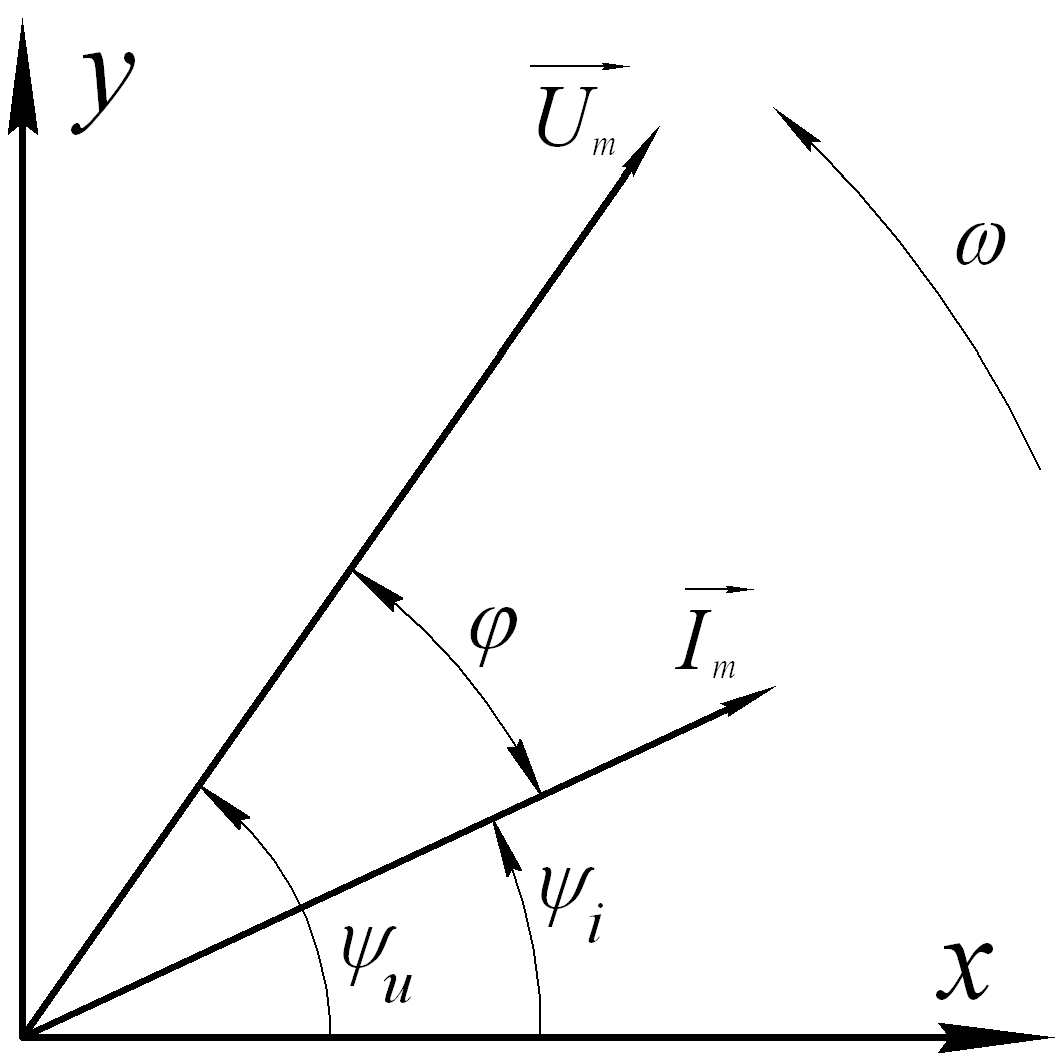Тогда в соответствии с выражениями (5.1) векторная диаграмма на декартовой плоскости будет иметь вид рис.5.4.

Представление синусоидальных величин одной и той же частоты в виде векторов называется векторной диаграммой.

Данная векторная диаграмма представлена в

момент времени t 0 , т.к. в противном случае

потребовалось бы записывать фазовые значения

Рис.5.4

напряжения и тока полностью ω tψ_u,

ω tψ_i.

Векторные диаграммы делают расчет цепей синусоидального тока простым и наглядным. Это достигается за счет того, что аналитическое сложение и вычитание

мгновенных значений синусоидальных величин можно заменить геометрическим сложением и вычитанием соответствующих им векторов.

Пусть, например, требуется найти сумму двух токов i₁

и i₂:

i₁ i₂ i₃.

Сумме двух синусоидальных функций одинаковой частоты соответствует также синусоидальная функция той же частоты

^Im1

 sin(ω tψ

₁)  I_m₂

 sin(ω tψ

₂)  I_m₃

 sin(ω tψ

₃).

Аналитически вычислить результирующие амплитуду

^Im3

и фазу ψ₃

достаточно сложно. Использование векторной диаграммы существенно упрощает процесс вычисления этих параметров.

Поскольку оба вектора вращаются с одинаковой угловой скоростью, и от

этого их взаимное расположение не меняется, то вектор общего тока

^Im3

равен

геометрической сумме векторов токов

I_m₁и

^Im2

(т.к. мгновенное значение общего

тока равно сумме проекций векторов на ось ординат рис.5.5).

Построение векторной диаграммы в масштабе позволяет определить непосредственно из диаграммы.
^Im3
и ψ₃

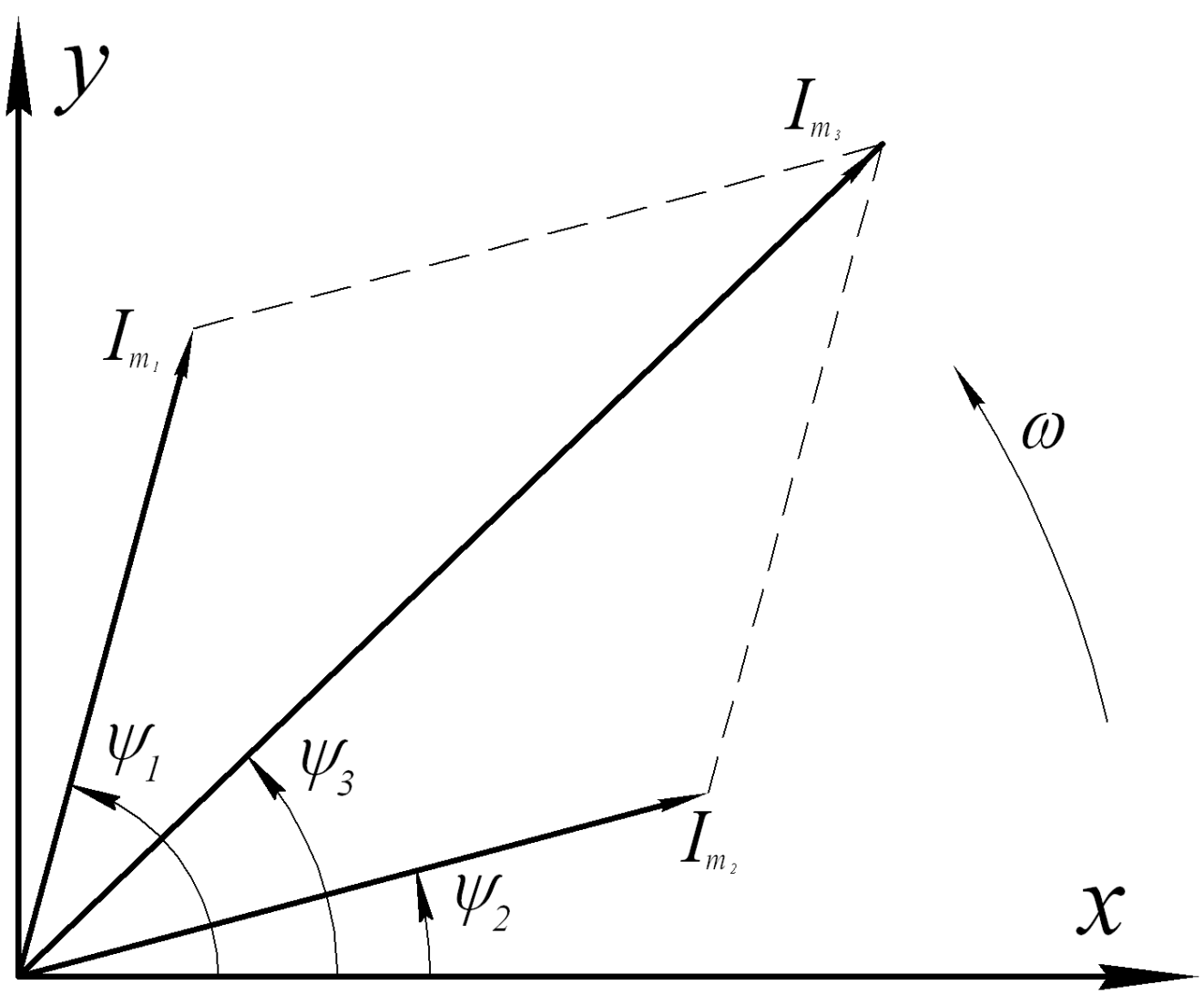
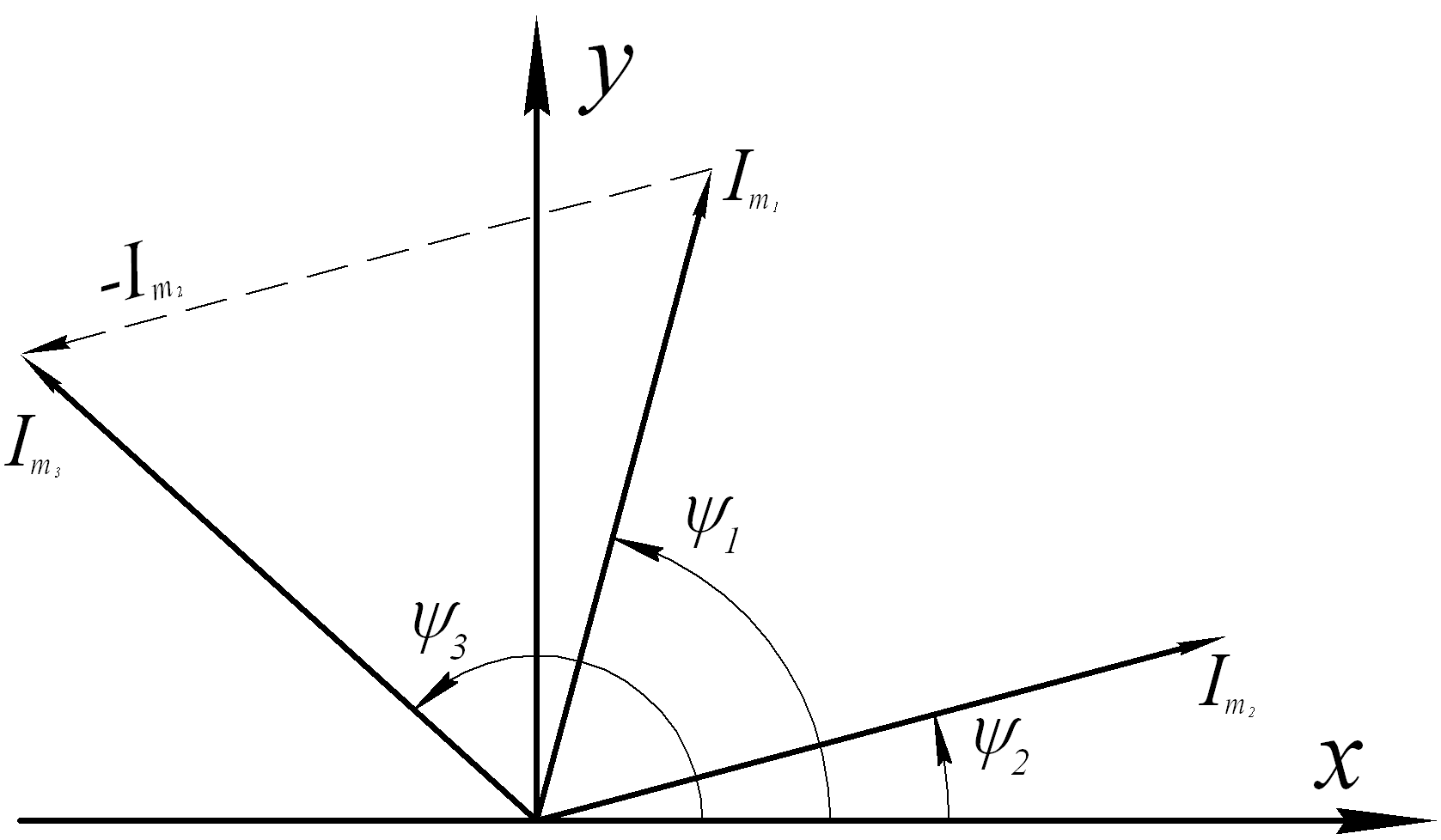Рис.5.5 _Рис.5.6

При определении разности этих двух токов:

i₃ i₁ i₂, складываются векторы

 I
I_m₁и обратный вектор _m₂(рис.5.6).

К недостаткам геометрического расчета электрических цепей с помощью векторных диаграмм следует отнести его невысокую точность и зависимость от субъективного фактора.

1 ... 13 14 15 16 17 18 19 20 ... 56

Представление синусоидальных величин комплексными числами

Чтобы перейти от декартовой к комплексной плоскости, ось абсцисс плоскости декартовых координат совмещают с осью действительных (вещественных) величин +1 комплексной плоскости.

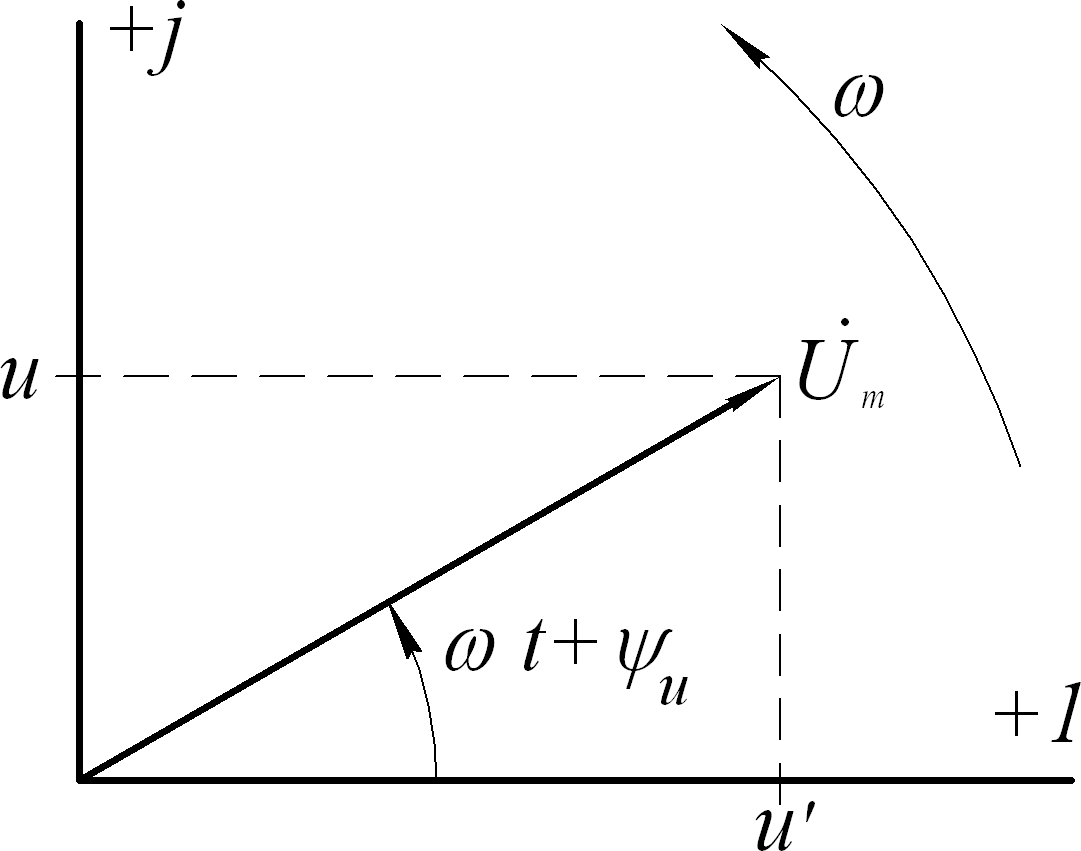Мгновенные значения синусоидальных величин получают на оси мнимых величин +j (рис.5.7).

Каждому вектору на комплексной плоскости соответствует комплексное число, которое может быть записано в показательной, тригонометрической или алгебраической форме.

Например, для напряжения

u U_msin(ω tψ_u) ,

Рис.5.7

изображенного на рис.5.7 получается комплексное число вида

m
_U__ej(ωtψ_u)

 U cos(ω tψ) 

jU sin(ω tψ)  u^

j u.

mu

mu
Фазовый угол ω tψ_u

определяется из соотношения:

^u tg(ω tψ

u^

_u) .

Мнимая составляющая комплексного числа определяет синусоидальное

u

m
изменение напряжения uи обозначается символом Im

u U_m

sin(ω t ψ

)  ImU

__ej(ωtψ_u) __,

а вещественная часть u^обозначается символом Re

m
u^ U_m cos(ω t ψ_u)  Re U

__ej(ωtψ_u) __.

m
Комплексное число произведения:

_U__ej(ωtψ_u)

удобно представить в виде следующего

m
_U__ej(ωtψ_u)

__U__ejψ_u__ejω t

__U___ejω t_,

m

m
где

U^_m– комплексная амплитуда, учитывающая положение вектора в начальный

момент времени;

_ejω t

– оператор поворота вектора на угол

ω t

относительно

начального положения.

Переход от одной формы записи к другой может быть выполнен по формуле Эйлера:

e^j^α cosα jsin α.

Пусть, например, комплексная амплитуда напряжения задана комплексным

числом в алгебраической форме:

U^_m U_m^

 jU_m^.

Чтобы записать ее в показательный

Смотрите также файлы

Дипломный проект на тему "Организация работы отделения по ремонту колесных пар пассажирского вагонного депо".docx

Жалпы білім беретін мектептердегі педагогдефектологты жаттары.docx

Фгбоу во тувинский государственный университет кызылский педагогический институт им. Народного писателя тувы а. А. Даржая.docx

Формирование морфологической стороны речи. Игры и упражнения с грамматическим содержанием для детей 34 лет.docx

Контрольная работа по дисциплине Инженерные изыскания при ведении кадастра.rtf

Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Представление синусоидальных величин комплексными числами

Смотрите также файлы

Информация

Списки файлов

Дополнительно