Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 377
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Ikk1
0.
(3.4)
Подставим (3.3) в (3.4) и выразим напряжение Uab:
n
(Ek
k1
n
Uab) gk
0;
(Ek gk
k1
n
Uab gk) 0;
n
Ek gk
k1
Uab gk
k1
n
Ek gk
0;
Uab
k1 .
n
gk
k1
Зная узловое напряжение Uab
очень просто получить все токи ветвей:
U
E U
1
1
1
ab
I 1 ab
R1
(E
) g;
k
k
U
ab
. . .
. . . .
. . . .
k
I Ek
Uab
Rk
(E
) g.
Метод эквивалентного генератора
Данный метод наиболее эффективен, когда требуется найти величину тока только в одной из ветвей сложной электрической цепи при различных значениях
сопротивления
Rxэтой ветви (на практике это встречается очень часто, например,
при настройке схем).
Пусть, например, дана цепь вида (рис.3.5).
Требуется определить ток Iв ветви с сопротивлением вызывается совместным действием ЭДС в левой части схемы.
Rx, который
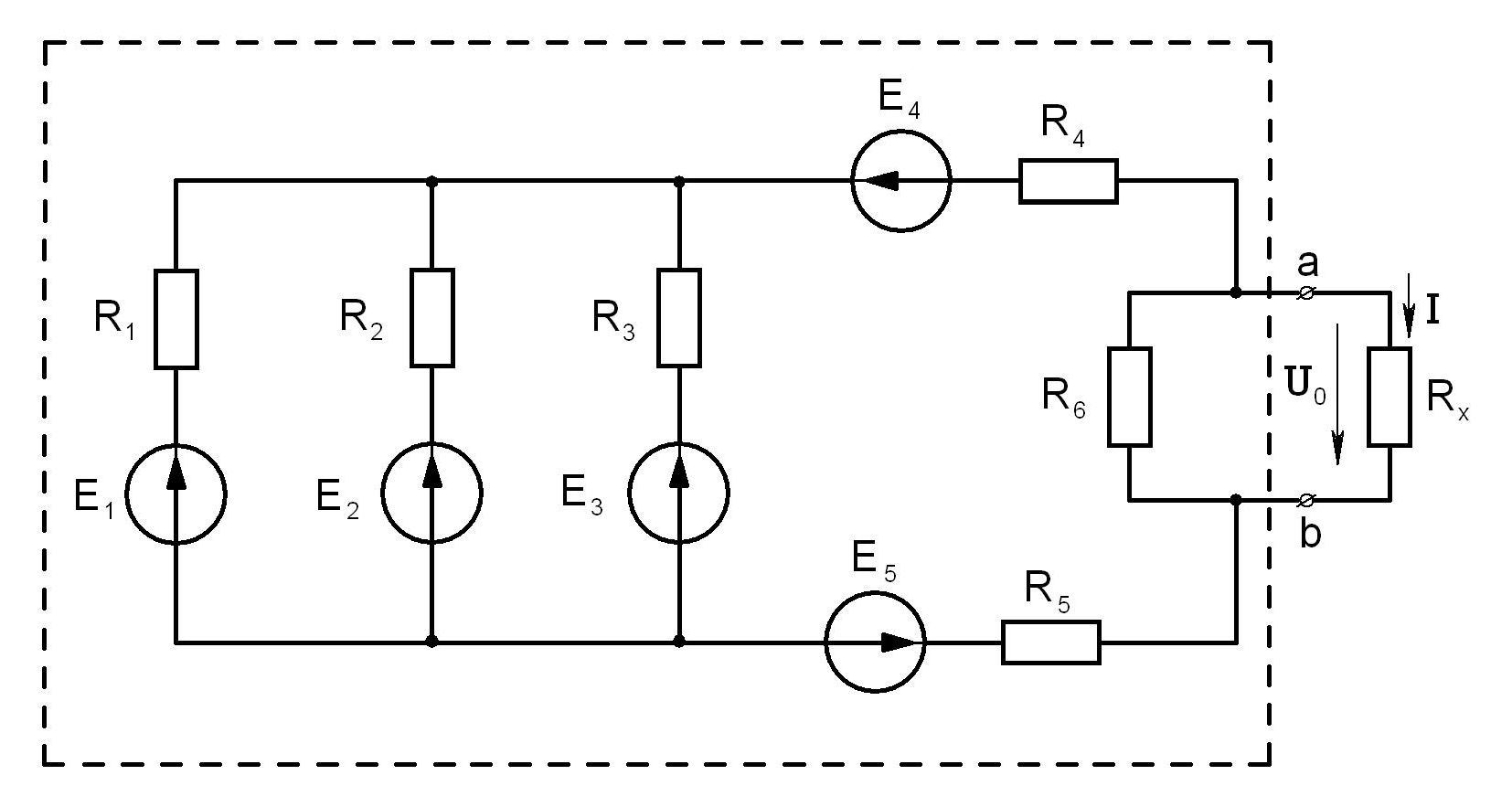
Рис.3.5
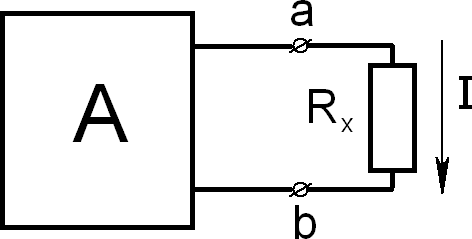
 Представим данную цепь в виде активного двухполюсника (рис.3.6).
Представим данную цепь в виде активного двухполюсника (рис.3.6).Рис.3.7
Рис.3.6
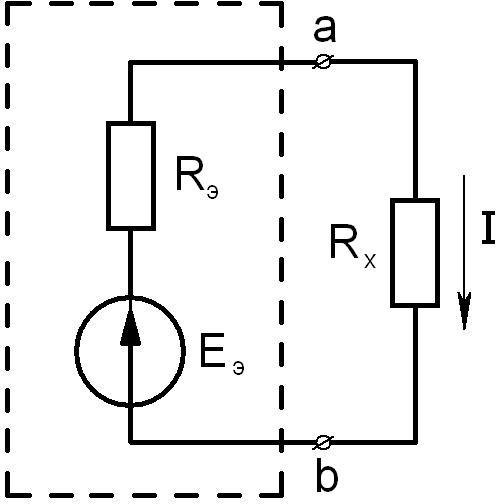
Суть метода заключается в том, чтобы заменить этот двухполюсник некоторой
эквивалентной ЭДС EЭ
с внутренним сопротивлением
RЭ(рис.3.7). Тогда искомый
ток Iможет быть определён по формуле
I EЭ.
RЭ Rx
Докажем возможность такой замены и определим EЭ
-
Разомкнем цепь в точке a (рис.3.8).
и RЭ.
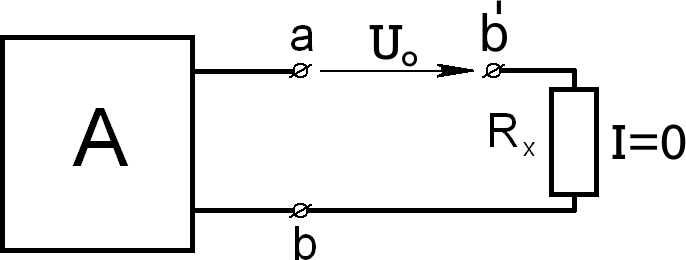
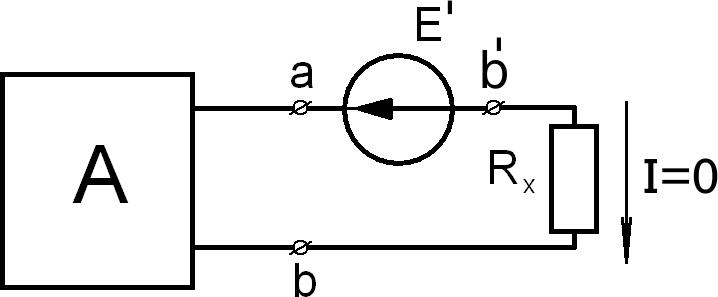
Рис.3.8 Рис.3.9
Тогда хода U0 .
I 0 , а между зажимами а и b′ будет действовать напряжение холостого
-
Между зажимами a и b′ включим ЭДС E , по величине равную напряжению
U0 , но направленную ему навстречу (рис.3.9). Очевидно, что ток через
сопротивление
Rxтакже будет равен нулю, т.е.
I 0 .
-
Введем в цепь дополнительную ЭДС E , равную и противоположную ЭДС
E (рис.3.10).
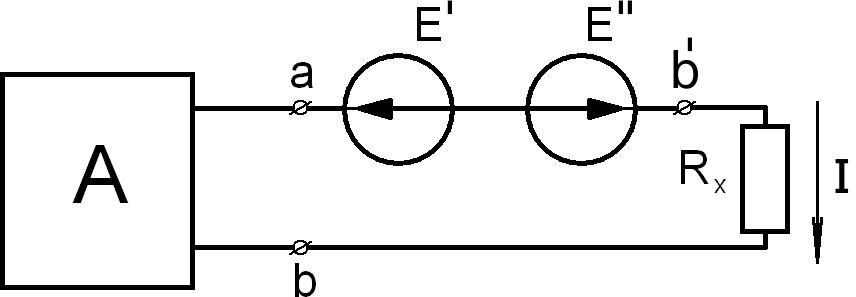
Рис.3.10
Очевидно, что эта схема на рис.3.17 эквивалентна первоначальной (рис.3.6), в
которой по сопротивлению
Rxпротекает ток I.
Отсюда следует, что
E E
U, т.е. эквивалентная ЭДС равна напряжению
0
Э
холостого хода на зажимах разомкнутой ветви, в которой определяется ток.
Напряжение холостого хода U0
определяется любым методом.
Следовательно,
I EЭ E
U0 .
RЭ RxRЭ Rx
RЭ Rx
В данной формуле
RЭпредставляет собой результирующее сопротивление
всей цепи двухполюсника найденное при условии, что все ЭДС равны нулю, а все сопротивления, включая и внутренние сопротивления ЭДС, остались неизменными
(т.е.
RЭ– есть входное сопротивление пассивного двухполюсника относительно
зажимов a и b).
Иногда целесообразно при расчётах (например, в схемах с электронными и полупроводниковыми элементами) заменить активный двухполюсник не
эквивалентной ЭДС, а эквивалентным источником тока. В этом случае неизменная
сила тока источника тока
IЭравна:
R
Э
I EЭ,
Э
а сопротивление
RЭподключается параллельно источнику тока.
- 1 ... 8 9 10 11 12 13 14 15 ... 56
Баланс мощности
Для проверки правильности выполненных расчётов составляется баланс мощности, реализующий, фактически, закон сохранения энергии в электрической
цепи. Из физики известно, что мощность связана с энергией выражением
Очевидно, что на единичном интервале времени ( t 1 c), W P.
W P.
t
В соответствии с законом сохранения энергии, энергия, поступающая в электрическую цепь от источников электрической энергии (ЭДС и тока), должна быть равна энергии, поступающей в приёмники (сопротивления R, индуктивности L и ёмкости C). Энергия, поступающая в сопротивление, выделяется на нём в виде
теплоты
Q I2 R1
в окружающее пространство, где I– ток, проходящий через
сопротивление. В индуктивности и ёмкости поступающая из источника энергия накапливается в виде энергии магнитного поля катушки и энергии электрического поля конденсатора соответственно.
Для линейной электрической цепи постоянного тока уравнение баланса активной мощности в общем случае имеет вид
n
E I
UJ J
I2 R,
m
kk
k1
k
k1
kkk
N
k1
где
Ek Ik– мощность, выдаваемая в цепь источниками ЭДС (если направление
действия ЭДС совпадает с направлением протекающего через него тока, то