ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.07.2024
Просмотров: 1362
Скачиваний: 0
СОДЕРЖАНИЕ
Создание маркированных и нумерованных списков
Оборудование, инструменты и приборы.
Варианты заданий для работы с нумерованными и маркированными списками
Варианты заданий для работы с многоуровневыми списками
Пример оформления практической части лабораторной работы № 1
Работа с математическими формулами
Оборудование, инструменты и приборы.
Пример оформления практической части лабораторной работы № 2
Вставка рисунков и диаграмм в документ
Оборудование, инструменты и приборы.
Варианты заданий для создания блок-схем, работы с надписями, выносками
Задания для текстовых эффектов с помощью WordArt
Варианты заданий для создания макросов
Пример оформления практической части лабораторной работы № 3
Лабораторная работа № 4 Слияние
Оборудование, инструменты и приборы.
Варианты заданий для создания документа с использованием слияния
Пример оформления практической части лабораторной работы № 4
Совместная работа Word с другими приложениями с помощью ole-технологии
Оборудование, инструменты и приборы.
Варианты заданий для работы с шаблонами
Варианты заданий для создания документа с использованием
Вставка и удаление строк и столбцов
Оборудование, инструменты и приборы.
Расчетная ведомость ао «темп» за июнь 1998г.
Оборудование, инструменты и приборы.
Количество осадков в миллиметрах
Количество осадков в миллиметрах
Количество осадков в миллиметрах по годам
Оплата за пользование телефоном
Оборудование, инструменты и приборы.
Организация ввода, просмотра и поиска данных с помощью форм
Примеры условий отбора расширенного фильтра
Подведение промежуточных итогов
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Раздел 3. Visual basic for Application (vba).
Правила построения блок–схемы алгоритма
Оборудование, инструменты и приборы.
Лабораторная работа №15 Редактор vba. Условный оператор. Подпрограммы
Оборудование, инструменты и приборы
Лабораторная работа № 16 Редактор vba. Оператор множественного ветвления
Оборудование, инструменты и приборы
Оборудование, инструменты и приборы
Программная реализация метода бисекции
”Задайте интервал, содержащий один корень”
Оборудование, инструменты и приборы
Редактор vba. Оператор цикла со счетчиком
Оборудование, инструменты и приборы
Лабораторная работа № 20 Редактор vba. Отладка программ. Пошаговое выполнение программы
Кнопки панели инструментов Debug
Оборудование, инструменты и приборы
3. Присваивание значений переменным
4. Задание ранжированной переменной
6. Определение и вычисление функции
8. Работа с векторами и матрицами:
Оборудование, инструменты и приборы
Лабораторная работа № 22 Построение графиков функций
Оборудование, инструменты и приборы
7. Символьное решение систем уравнений
Оборудование, инструменты и приборы
3. Одномерная линейная аппроксимация
4. Одномерная сплайн-интерполяция
6. Функции предсказания данных.
Оборудование, инструменты и приборы
Задание 4
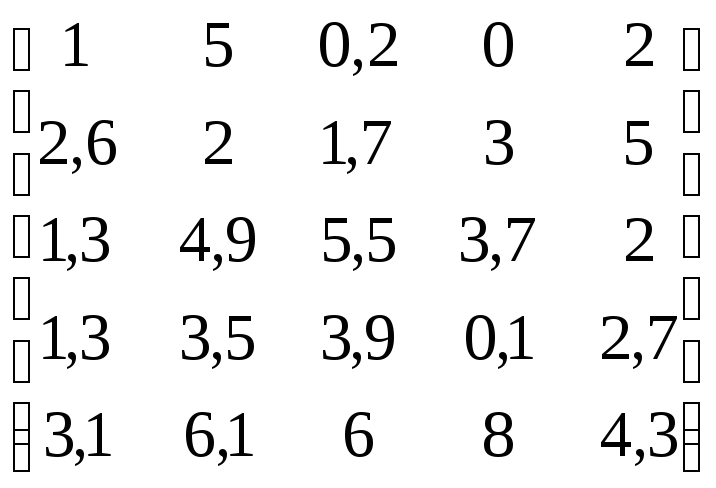
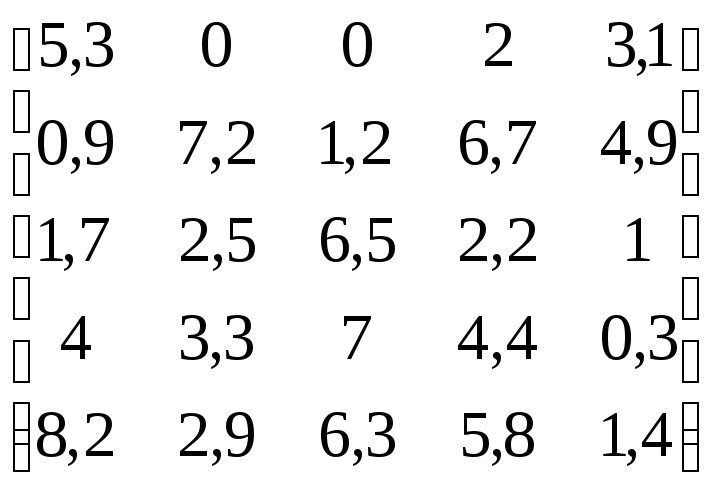
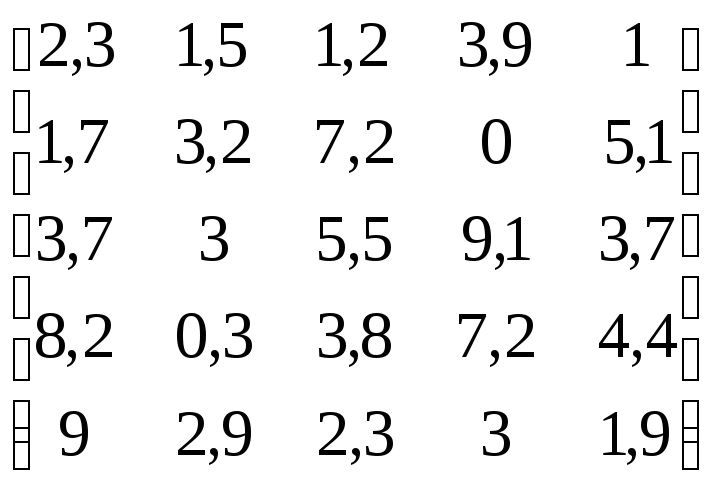
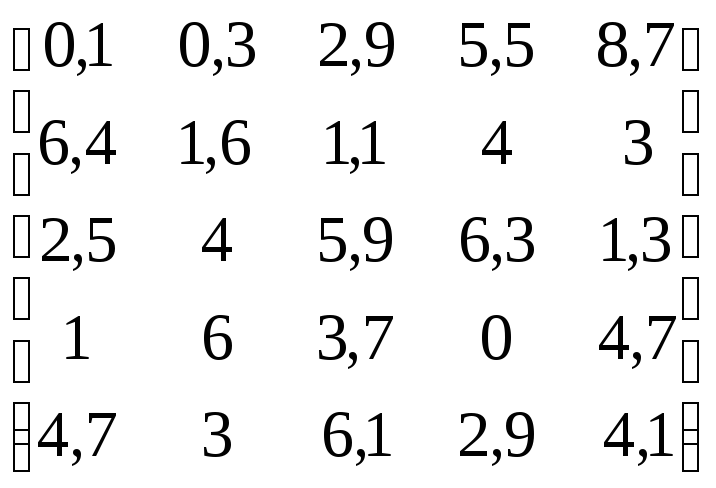
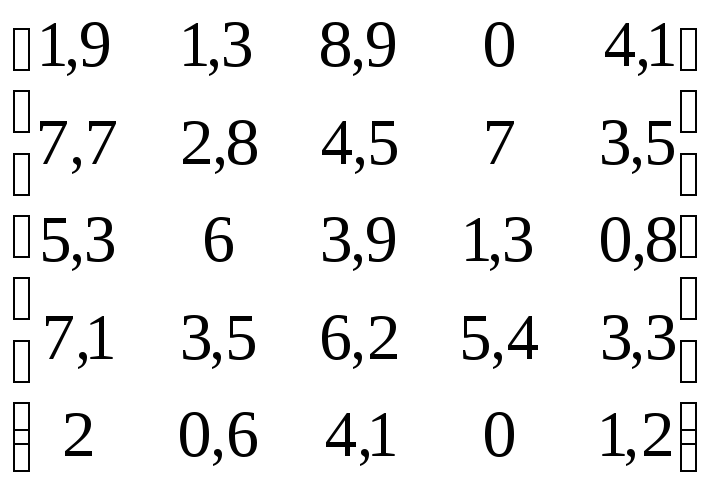
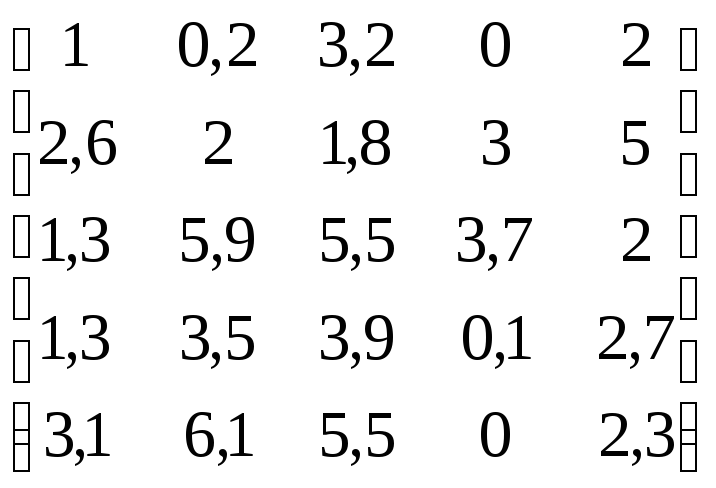
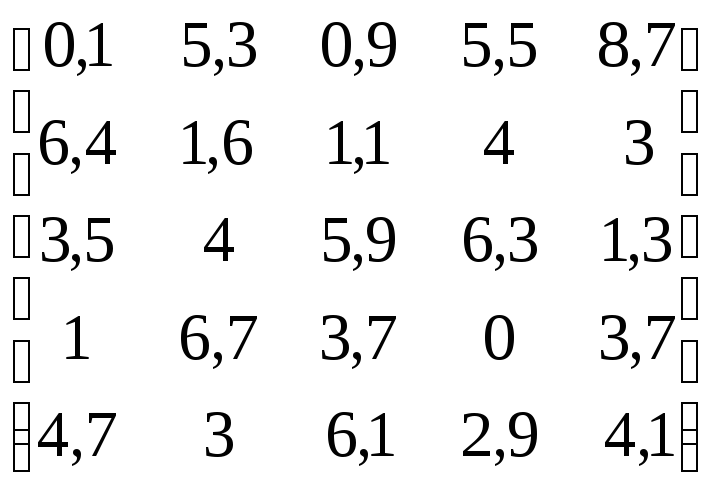
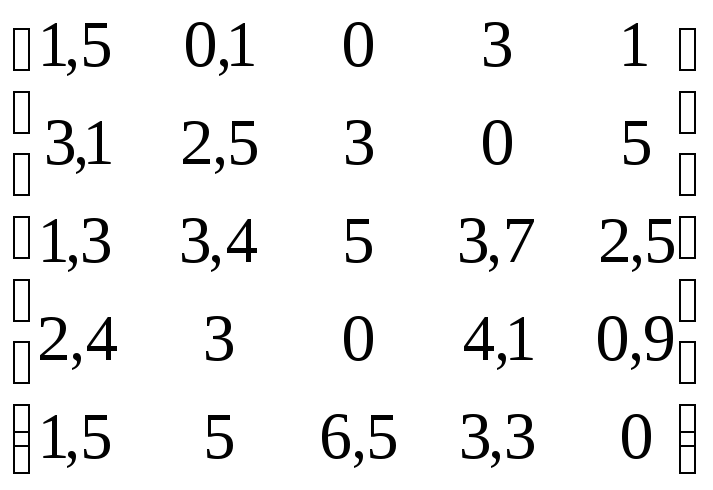
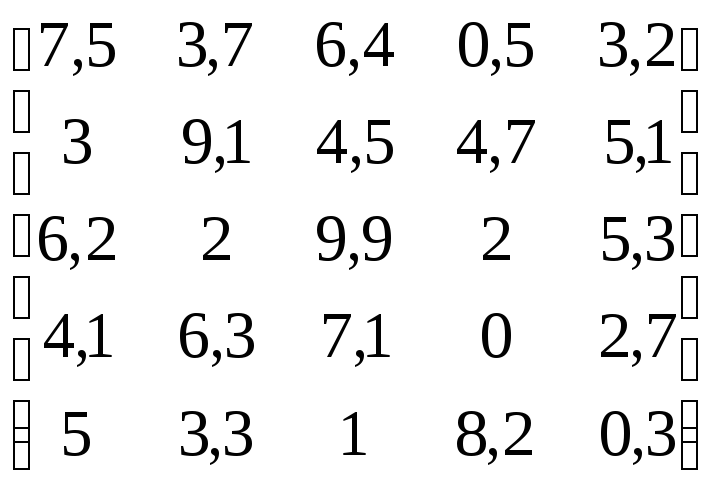
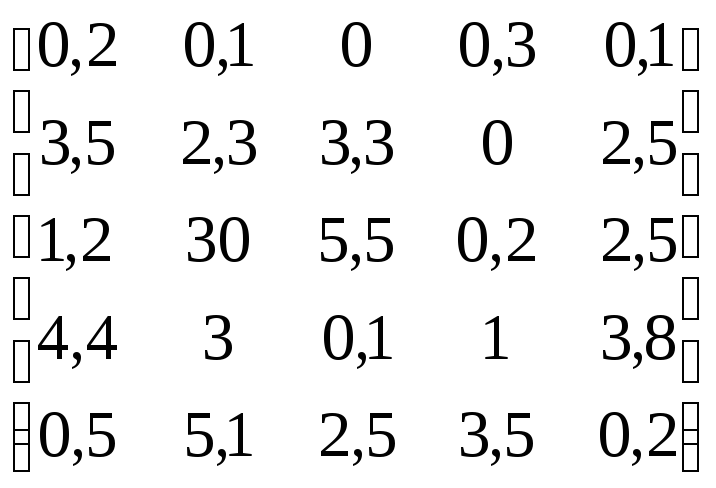
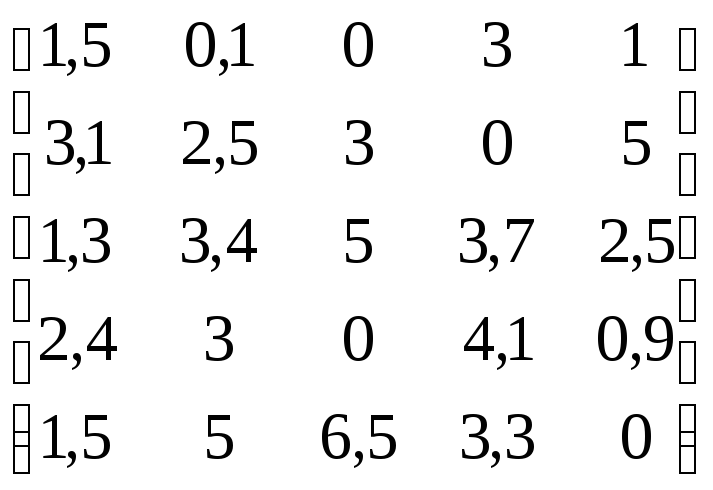
В соответствии с данными, приведенными в табл.4.11:
Построить график поверхности, заданный матрицей.
Построить график линий уровня, заданный матрицей.
Построить столбиковую диаграмму, заданную матрицей.
Построить точечный график, заданный матрицей.
Таблица 4.11
Варианты заданий
|
№ вар |
Задание |
№ вар |
Задание |
№ вар |
Задание |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
z= |
11 |
z= |
21 |
z= |
|
2 |
z= |
12 |
z= |
22 |
z= |
|
3 |
z= |
13 |
z= |
23 |
z= |
|
4 |
z= |
4 |
z= |
24 |
z= |
Продолжение табл. 4.11
|
1 |
2 |
3 |
4 |
5 |
6 |
|
5 |
z= |
15 |
z= |
25 |
z= |
|
6 |
z= |
16 |
z= |
26 |
z= |
|
7 |
z= |
17 |
z= |
27 |
z= |
|
8 |
z= |
18 |
z= |
28 |
z= |
|
9 |
z= |
19 |
z= |
29 |
z= |
|
10 |
z= |
20 |
z= |
30 |
z= |
Задание 5
Скопировать график 1 (рис. 60) и изменить его вид.
Порядок выполнения работы
Создать MathCad – документ и сохранить его под именем «Графики».
Выполнить задания 1 – 5 в соответствии с данными своего варианта
Содержание отчета
Отчет должен содержать:
номер, название и цель работы;
краткую теоретическую часть, включающую порядок построения двумерных и трехмерных графиков;
результаты выполнения работы согласно заданию, выданному преподавателем, а именно, в отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “ Графики ”;
заключение по работе.
Контрольные вопросы
Подготовка построения графиков.
Построение графика в декартовой системе координат.
Построение графика в полярной системе координат.
Построение трехмерных графиков.
Построить график по указанию преподавателя.
ЛАБОРАТОРНАЯ РАБОТА № 23
Решение уравнений и систем уравнений
Цель работы: научиться решать нелинейные уравнения и системы линейных и нелинейных уравнений.
Теоретическая часть
Решение нелинейных уравнений
Многие уравнения не имеют аналитических решений. Однако многие из них могут решаться численными методами с заданной погрешностью. Для простейших уравнений вида F(x)=0 решение находится с помощью функции
root(Выражение, имя переменной)
Эта функция возвращает значение переменной, при котором выражение равно нулю с заданной точностью. Функция реализует вычисление итерационным методом. Необходимо задать начальное значение переменной. В зависимости от заданного начального приближения к корню находится ближайший корень. Функция root находит только один корень, ближайший к заданному начальному значению. Для отыскания всех корней необходимо задавать различные значения начальных приближений. Функция root может отыскивать и комплексные корни. Недостатком функции root является невозможность решения с ее помощью систем нелинейных уравнений. На рис.61 приведен пример применения функции root. Точность решения задается переменной TOL. По умолчанию задается точность 0,001.Если точность выше 0,001, то требуется изменить количество знаков после запятой при выводе вещественных чисел по команде Format.

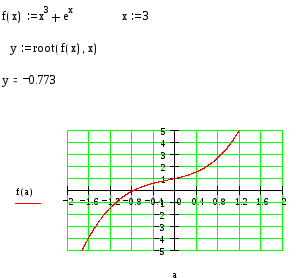
Рис.61. Пример решения нелинейного уравнения с применением функции root
Решение уравнений полиномиального вида
Для поиска корней обычного полинома р(х) степени n MathCad содержит очень удобную функцию
polyroot(V)
Она возвращает вектор всех корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину, равную n+1.
Корни полинома могут быть как вещественными, так и комплексными. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, в этом случае трудно получить малую погрешность вычисления корней.
На рис.62 приведен пример применения функции polyroot.

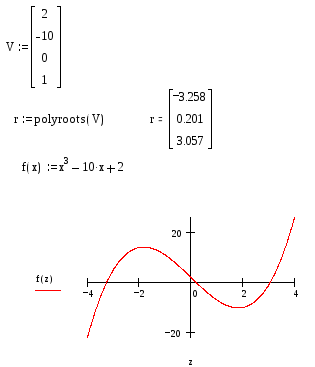
Рис.62. Пример решения уравнения полиномиального вида на примере применения функции polyroot
Символьное решение уравнений
Для выполнения символьных вычислений MathCad дополнен символьным процессором, операции которого содержатся в подменю позиции Simbolic главного меню. Можно открыть таблицу символьных операций из математического меню.
Функция
solve,x
позволяет найти значение обозначенной переменной, при которой содержащее ее выражение становится равным нулю.
На рис.63 приведен пример применения функции solve. Чтобы поставить знак =, нужно одновременно нажать Ctrl и знак = или воспользоваться специальной палеткой для набора знаков.

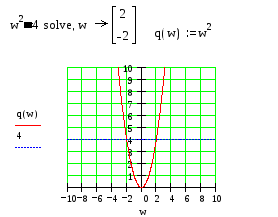
Рис.63. Пример символьного решения нелинейного уравнения с применением функции solve
Решение систем линейных уравнений с помощью функции lsolve
Для решения систем линейных уравнений в MathCad введена встроенная функция
lsolve(A,B),
которая возвращает вектор Х для системы линейных уравнений А*Х=В при заданной матрице коэффициентов А и векторе свободных членов В.
На рис.64 приведены примеры применения функции lsolve.

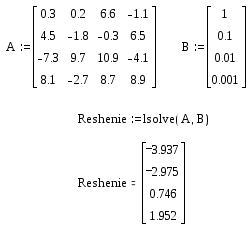
Рис.64. Пример символьного решения системы линейных уравнений с применением функции lsolve
Решение систем линейных уравнений в матричной форме.
Векторные и матричные операторы и функции системы MathCad позволяют решать широкий круг задач линейной алгебры.
Для
системы линейных уравнений А*Х=В
при заданной матрице коэффициентов А
и векторе
свободных членов
В вектор
решения можно получить из очевидного
выражения Х=В*А![]() .
.
На рис.65 приведен пример решения систем линейных уравнений в матричной форме.


Рис.65. Пример матричного решения системы линейных уравнений
6. Решение нелинейных уравнений и их систем
При решении нелинейных уравнений и их систем используется специальный вычислительный блок, открываемый служебным словом-директивой Given, которое набирается с клавиатуры. До начала блока задаются начальные приближения к неизвестным переменным. Внутри блока записывается уравнение или система уравнений. Для решения систем нелинейных уравнений используется одна из двух следующих функций:
find(v1,v2...vn) - возвращает значение одной или нескольких переменных для точного решения;
minerr(v1,v2...vn) - возвращает значение одной или нескольких переменных для приближенного решения.
Между этими двумя функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.