ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.07.2024
Просмотров: 1329
Скачиваний: 0
СОДЕРЖАНИЕ
Создание маркированных и нумерованных списков
Оборудование, инструменты и приборы.
Варианты заданий для работы с нумерованными и маркированными списками
Варианты заданий для работы с многоуровневыми списками
Пример оформления практической части лабораторной работы № 1
Работа с математическими формулами
Оборудование, инструменты и приборы.
Пример оформления практической части лабораторной работы № 2
Вставка рисунков и диаграмм в документ
Оборудование, инструменты и приборы.
Варианты заданий для создания блок-схем, работы с надписями, выносками
Задания для текстовых эффектов с помощью WordArt
Варианты заданий для создания макросов
Пример оформления практической части лабораторной работы № 3
Лабораторная работа № 4 Слияние
Оборудование, инструменты и приборы.
Варианты заданий для создания документа с использованием слияния
Пример оформления практической части лабораторной работы № 4
Совместная работа Word с другими приложениями с помощью ole-технологии
Оборудование, инструменты и приборы.
Варианты заданий для работы с шаблонами
Варианты заданий для создания документа с использованием
Вставка и удаление строк и столбцов
Оборудование, инструменты и приборы.
Расчетная ведомость ао «темп» за июнь 1998г.
Оборудование, инструменты и приборы.
Количество осадков в миллиметрах
Количество осадков в миллиметрах
Количество осадков в миллиметрах по годам
Оплата за пользование телефоном
Оборудование, инструменты и приборы.
Организация ввода, просмотра и поиска данных с помощью форм
Примеры условий отбора расширенного фильтра
Подведение промежуточных итогов
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Раздел 3. Visual basic for Application (vba).
Правила построения блок–схемы алгоритма
Оборудование, инструменты и приборы.
Лабораторная работа №15 Редактор vba. Условный оператор. Подпрограммы
Оборудование, инструменты и приборы
Лабораторная работа № 16 Редактор vba. Оператор множественного ветвления
Оборудование, инструменты и приборы
Оборудование, инструменты и приборы
Программная реализация метода бисекции
”Задайте интервал, содержащий один корень”
Оборудование, инструменты и приборы
Редактор vba. Оператор цикла со счетчиком
Оборудование, инструменты и приборы
Лабораторная работа № 20 Редактор vba. Отладка программ. Пошаговое выполнение программы
Кнопки панели инструментов Debug
Оборудование, инструменты и приборы
3. Присваивание значений переменным
4. Задание ранжированной переменной
6. Определение и вычисление функции
8. Работа с векторами и матрицами:
Оборудование, инструменты и приборы
Лабораторная работа № 22 Построение графиков функций
Оборудование, инструменты и приборы
7. Символьное решение систем уравнений
Оборудование, инструменты и приборы
3. Одномерная линейная аппроксимация
4. Одномерная сплайн-интерполяция
6. Функции предсказания данных.
Оборудование, инструменты и приборы
Оборудование, инструменты и приборы
ПЭВМ, система MathCad
Варианты заданий
Варианты заданий приведены в таблицах 4.16 -4.17.
Задание 1
Найти частное решение y(x) дифференциального уравнения для своего варианта при произвольных начальных условиях и построить график решения. Варианты заданий приведены в табл.4.16.
Таблица 4.16
Варианты заданий
|
№ вар |
Задание |
№ вар |
Задание |
№ вар |
Задание |
|
1 |
yIII-13yII+12yI=0 |
11 |
yIII+y=0 |
21 |
4yII+y=x |
|
2 |
yIII-3yII+3yI-y=0 |
12 |
yIV+8yII+16y=0 |
22 |
2yIII-x yI=cox x+y |
|
3 |
yIV-3yII+y=0 |
13 |
yIV+2yIII+yII=0 |
23 |
7yII+3yI-2xy=0 |
|
4 |
yIV-2yIII+yII=ex |
14 |
yIII-y=x3-1 |
24 |
3yII+y=sin2x |
|
5 |
yIII+yII=x2+1+3xex |
15 |
yIV+yIII=cos 4x |
25 |
yI+3yII=xex |
|
6 |
yII-2y=2xex(cos x –sinx) |
16 |
yII+y=1/cos x |
26 |
yIII-3yII=y+x2 |
|
7 |
yII+y=2x cos x cos 2x |
17 |
x2 yII+x yI-y=x2 |
27 |
(x+5)yIII+3yI=x+1 |
|
8 |
(x+1)yII+x(yI)2=yI |
18 |
(1+y yI)yII=1+(yI)2 |
28 |
yII+3yI=cos x+2 |
|
9 |
2yI+ex yII=3-x |
19 |
(1+y)yII+3=2sin 2x |
29 |
yIII+yII-3yI=y+x ln x |
|
10 |
2yII-3x yI+7y=(x+1)2 |
20 |
yII-(1+y)yI=2+x2 |
30 |
yIII+2yII=sin x |
Задание 2
Решите систему дифференциальных уравнений для своего варианта на отрезке [0,3]. Выведите значения искомых функций и их производных в точке с координатой х=1.5. Варианты заданий приведены в табл.4.17.
Таблица 4.17
Варианты заданий
|
№ вар |
Задание |
№ вар |
Задание |
|
1 |
xI=y-x2-x x(0)=0 yI=3x-x2-y y(0)=1 |
16 |
xI=sin y-x x(0)=0 yI=x-y2 y(0)=1 |
|
2 |
xII=x-3y x(0)=0 xI(0)=3 yII=x+2y y(0)=1 xI(0)=-1 |
17 |
xII=x+3y x(0)=3 xI(0)=5 yII=2y-x y(0)=2 xI(0)=-2 |
|
3 |
xI= y-ex x(0)=0 yI= 2ex-y y(0)=1 |
18 |
xI=2y-x x(0)=0 yI=cos x-2y2 y(0)=1 |
|
4 |
xII=5x-3y x(0)=-2 xI(0)=5 yII=3x+2y y(0)=2 xI(0)=2 |
19 |
xII=4x-3y x(0)=0 xI(0)=1 yII=x-2y y(0)=2 xI(0)=-1 |
|
5 |
xI=2y-x2+x x(0)=1 yI=3x-y y(0)=1 |
20 |
xII=2x-3y x(0)=0 xI(0)=5 yII=x-2y y(0)=2 xI(0)=-1 |
|
6 |
xI=2sin y+x2 x(0)=0 yI=3x-y2-y y(0)=1 |
21 |
xI= y-xey x(0)=1 yI= 2ey-y y(0)=1 |
|
7 |
xII=x-y x(0)=0 xI(0)=5 yII=x+3y y(0)=2 xI(0)=-1 |
22 |
xII=2x-y x(0)=0 xI(0)=5 yII=2y y(0)=-1 xI(0)=2 |
|
8 |
xI=2y-x2 x(0)=0 yI=3x-y2-y y(0)=-1 |
23 |
xII=2x-3y+1 x(0)=0 xI(0)=3 yII=x-2 y(0)=2 xI(0)=1 |
|
9 |
xII=1+3y x(0)=0 xI(0)=1 yII=x-2y y(0)=2 xI(0)=-1 |
24 |
xI=y-x x(0)=0 yI=cos x-y2 y(0)=1 |
|
10 |
xI=2y-2x2-2x x(0)=-1 yI=3x2-y y(0)=0 |
25 |
xI=y-3x x(0)=0 yI=3x-x2-y y(0)=1 |
|
11 |
xII=2-y x(0)=0 xI(0)=5 yII=x y(0)=2 xI(0)=-1 |
26 |
xI= 2y-ex x(0)=0 yI= ex-y y(0)=1 |
|
12 |
xI=sin y-x x(0)=0 yI=cos x-y2 y(0)=1 |
27 |
xI=sin x-2y x(0)=0 yI=3x-y2 y(0)=1 |
|
13 |
xI=3y-x2 x(0)=0 yI=2x-y2 y(0)=1 |
28 |
xI=y-x2 x(0)=0 yI=3x-y2-y y(0)=-1 |
|
14 |
xI=y-2x2-2 x(0)=0 yI=x-y2 y(0)=-1 |
29 |
xI=sin x-x x(0)=0 yI=x-y2 y(0)=1 |
|
15 |
xI=y-x2 x(0)=2 yI=x-3y2 y(0)=1 |
30 |
xII=x-3y x(0)=0 xI(0)=1 yII=x-2y y(0)=2 xI(0)=-1 |
Задание 3
Решить задачу, рассмотренную в пункте 8 с учетом данных своего варианта. Для вариантов 1 – 5: tk=45с, для вариантов 6 – 10: tk=40с, для вариантов 11 – 15: tk=50с, для вариантов 16 – 20: tk=55с, для вариантов 21 – 25: tk=35с, для вариантов 26 – 30: tk=30с.
Порядок выполнения работы.
Создать MathCad – документ и сохранить его под именем «Решение_дифф_уравнений_систем».
Выполнить задания в соответствии с данными своего варианта.
Содержание отчета.
В отчете по лабораторной работе должно быть дано описание методов решения дифференциальных уравнений и систем.
В отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “Решение_ дифф_уравнений_систем”.
Контрольные вопросы.
При помощи каких функций решаются нелинейные дифференциальные уравнения?
При помощи каких функций решаются системы дифференциальных уравнений?
Решить дифференциальное уравнение по заданию преподавателя.
Решить систему дифференциальных уравнений по заданию преподавателя.
Лабораторная работа № 25
Выполнение регрессии и проведение аппроксимации. Функции сглаживания данных и предсказания.
Цель работы: Научиться выполнять обработку данных с помощью методов регрессии и аппроксимации, заложенных в MathCad.
Теоретическая часть
Выполнение регрессии
Широко распространенной задачей обработки данных является представление их совокупности некоторой функцией y(x). Задача регрессии заключается в представлении параметров этой функции такими, чтобы функция приближала бы облако исходных точек (заданных векторами VX и VY) с наименьшей среднеквадратичной погрешностью.
Проведение линейной и сплайновой аппроксимаций
Для представления физических закономерностей и при проведении научно-технических расчетов часто используются зависимости вида y(x), причем число точек этих зависимостей ограничено. Неизбежно возникает задача приближенного вычисления значений функций в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией исходной зависимости, т. е. ее подменой какой-либо достаточно простой функцией. Система Mathcad представляет возможность аппроксимации двумя важными типами функций: кусочно-линейной и сплайновой.
Выполнение линейной регрессии
Чаще всего используется линейная регрессия, при которой функция y(x) имеет вид: y(x)=a+bx и описывает отрезок прямой.
Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций:
corr(VX,VY) - возвращает скаляр - коэффициент корреляции Пирсона;
intercept(VX,VY) - возвращает значение параметра a (смещение линии регрессии по вертикали);
slope(VX,VY) - возвращает значение параметра b (угловой коэффициент линии регрессии).
На рис.70 показан пример проведения линейной регрессии для данных, представленных значениями элементов в векторах VX и VY.
Как видно из рисунка, прямая регрессия проходит в «облаке» исходных точек с максимальным среднеквадратичным приближением к ним. Чем ближе коэффициент корреляции к 1, тем точнее представленная исходными точками зависимость приближается к линейной.
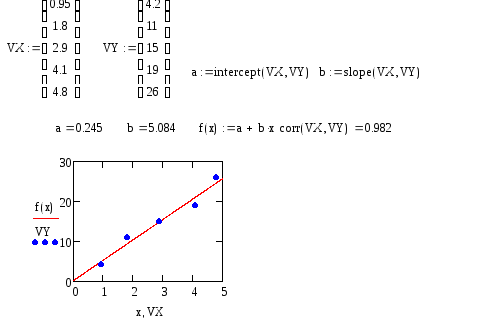
Рис.70. Пример проведения линейной регрессии