ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.07.2024
Просмотров: 1318
Скачиваний: 0
СОДЕРЖАНИЕ
Создание маркированных и нумерованных списков
Оборудование, инструменты и приборы.
Варианты заданий для работы с нумерованными и маркированными списками
Варианты заданий для работы с многоуровневыми списками
Пример оформления практической части лабораторной работы № 1
Работа с математическими формулами
Оборудование, инструменты и приборы.
Пример оформления практической части лабораторной работы № 2
Вставка рисунков и диаграмм в документ
Оборудование, инструменты и приборы.
Варианты заданий для создания блок-схем, работы с надписями, выносками
Задания для текстовых эффектов с помощью WordArt
Варианты заданий для создания макросов
Пример оформления практической части лабораторной работы № 3
Лабораторная работа № 4 Слияние
Оборудование, инструменты и приборы.
Варианты заданий для создания документа с использованием слияния
Пример оформления практической части лабораторной работы № 4
Совместная работа Word с другими приложениями с помощью ole-технологии
Оборудование, инструменты и приборы.
Варианты заданий для работы с шаблонами
Варианты заданий для создания документа с использованием
Вставка и удаление строк и столбцов
Оборудование, инструменты и приборы.
Расчетная ведомость ао «темп» за июнь 1998г.
Оборудование, инструменты и приборы.
Количество осадков в миллиметрах
Количество осадков в миллиметрах
Количество осадков в миллиметрах по годам
Оплата за пользование телефоном
Оборудование, инструменты и приборы.
Организация ввода, просмотра и поиска данных с помощью форм
Примеры условий отбора расширенного фильтра
Подведение промежуточных итогов
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Оборудование, инструменты и приборы.
Раздел 3. Visual basic for Application (vba).
Правила построения блок–схемы алгоритма
Оборудование, инструменты и приборы.
Лабораторная работа №15 Редактор vba. Условный оператор. Подпрограммы
Оборудование, инструменты и приборы
Лабораторная работа № 16 Редактор vba. Оператор множественного ветвления
Оборудование, инструменты и приборы
Оборудование, инструменты и приборы
Программная реализация метода бисекции
”Задайте интервал, содержащий один корень”
Оборудование, инструменты и приборы
Редактор vba. Оператор цикла со счетчиком
Оборудование, инструменты и приборы
Лабораторная работа № 20 Редактор vba. Отладка программ. Пошаговое выполнение программы
Кнопки панели инструментов Debug
Оборудование, инструменты и приборы
3. Присваивание значений переменным
4. Задание ранжированной переменной
6. Определение и вычисление функции
8. Работа с векторами и матрицами:
Оборудование, инструменты и приборы
Лабораторная работа № 22 Построение графиков функций
Оборудование, инструменты и приборы
7. Символьное решение систем уравнений
Оборудование, инструменты и приборы
3. Одномерная линейная аппроксимация
4. Одномерная сплайн-интерполяция
6. Функции предсказания данных.
Оборудование, инструменты и приборы
Реализация линейной регрессии общего вида
В MathCad 7 реализована возможность выполнения линейной регрессии общего вида. При ней заданная совокупность точек приближается функцией вида: F(x,K1,K1,...,KN)=K1*F1(x)+K2*F2(x)+...+KN*FN(x).
Таким образом, функция регрессии является линейной комбинацией функций F1(x),F2(x)...FN(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции.
Для реализации линейной регрессии общего вида используется функция:
linfit(VX,VY,F) - возвращает вектор коэффициентов линейной регрессии К, при котором среднеквадратичная погрешность приближения «облака» исходных точек, координаты которых хранятся в векторах VX и VY, оказывается минимальной. Вектор должен содержать функции F1(x),F2(x)...FN(x), записанные в символьном виде.
Рис.71 поясняет проведение линейной регрессии общего вида с применением функции linfit.
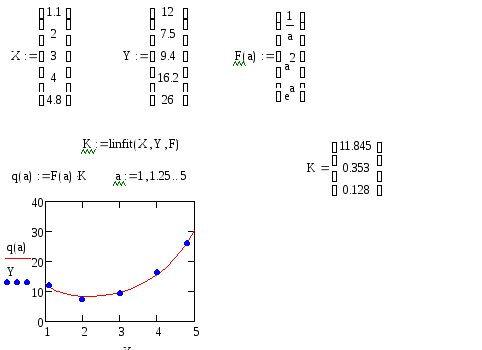
Рис.71. Пример проведения линейной регрессии общего вида
3. Одномерная линейная аппроксимация
При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение узловых точек отрезками прямых, для чего используется следующая функция:
linterp(VX,VY,x).
Для заданных векторов VX и VY узловых точек и заданного аргумента х linterp(VX,VY,x) возвращает значение функции при ее линейной аппроксимации. При экстраполяции используются отрезки прямых, проведенные через две крайние точки.
4. Одномерная сплайн-интерполяция
При небольшом количестве узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp(VX,VY,x) не предназначена и за пределами области определения может вести себя непредсказуемо.
Гораздо лучшие результаты дает сплайн-аппроксимация. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках (откуда и название аппроксимации spline - гибкая линейка).
Для осуществления сплайновой аппроксимации система Mathcad предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн-функций при различном виде интерполяции:
cspline(VX,VY) - возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;
pspline(VX,VY) - возвращает вектор VS вторых производных при приближении в опорных точках к параболической кривой;
lspline(VX,VY) - возвращает вектор VS вторых производных при приближении к опорным точкам прямой.
Наконец, четвертая функция
interp(VS,VX,VY,x) - возвращает значение y(x) для заданных векторов VS,VX,VY и заданного значения x.
На рис. 72 приведены примеры линейной и сплайновой аппроксимаций функции.
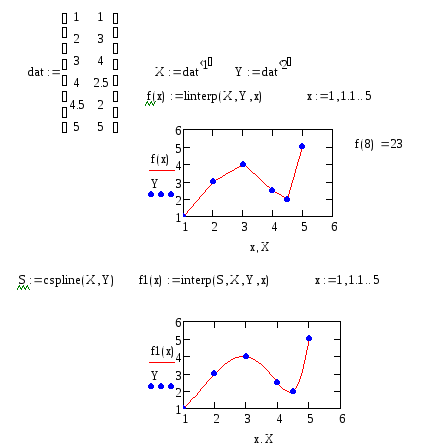
Рис.72. Примеры линейной и сплайновой аппроксимаций
5. Функции сглаживания данных
Данные большинства экспериментов имеют случайные составляющие погрешности. Поэтому часто возникает необходимость статистического сглаживания данных. Ряд функций MathCAD предназначен для выполнения операций сглаживания данных различными методами (рис. 72). Вот перечень этих функций:
medsmooth(VY,n)— для вектора с m действительными числами возвращает m-мерный вектор сглаженных данных по методу скользящей медианы, параметр n задает ширину окна сглаживания (n должно быть нечетным числом, меньшим m);
ksmooth(VX, VY, b) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе распределения Гаусса. VX и VY — n-мерные векторы действительных чисел. Параметр b (полоса пропускания) задает ширину окна сглаживания ( b должно в несколько раз превышать интервал между точками по оси х );
supsmooth(VX, VY) — возвращает n-мерный вектор сглаженных VY, вычисленных на основе использования процедуры линейного сглаживания методом наименьших квадратов по правилу k-ближайших соседей с адаптивным выбором k. VX и VY — n-мерные векторы действительных чисел. Элементы вектора VX должны идти в порядке возрастания.
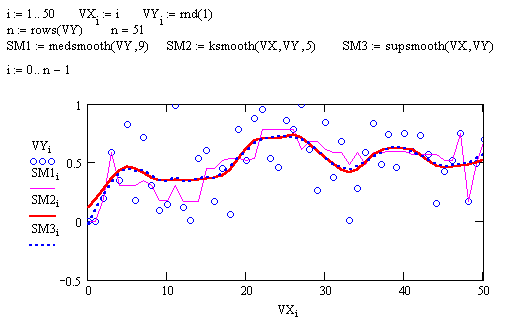
Рис.73. Пример применения функций сглаживания случайных данных.
6. Функции предсказания данных.
Весьма интересной является функция предсказания predikt(data,k,N), где data — вектор данных, где data — вектор данных, k — число последних точек существующих данных, на основе которых происходит расчет предсказываемых точек; и N — число точек, в которых необходимо предсказать данные. Она по ряду заданных равномерно расположенных точек позволяет рассчитать некоторое число N последующих точек, т. е. по существу выполняет экстраполяцию произвольной (но достаточно гладкой и предсказуемой) зависимости.
Функция предсказания обеспечивает высокую точность при монотонных исходных функциях или функциях, представляемых полиномом невысокой степени (рис. 74).
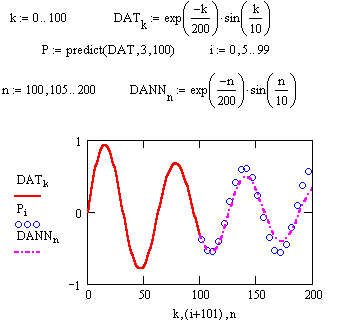
Рис. 74. Пример применения функции предсказания случайных данных.
Оборудование, инструменты и приборы
ПЭВМ, система MathCad
Варианты заданий
Варианты заданий приведены в таблице 4.18.
Задание 1
Введите матрицу координат точек на плоскости согласно № варианта.
Таблица 4.18
Варианты заданий
|
Вар № |
Задание |
Вар № |
Задание |
||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
Окончание табл. 4. 18
|
1 |
2 |
3 |
4 |
||||||||||||||||||||||||||||||
|
|
|
|
|