Файл: Теория игр для экономистов doc.doc

Если седловой точки нет, то решение необходимо искать в смешанных стратегиях.

.

Оптимальная смешанная стратегия находится из решения задачи линейного программирования

A^T X≥V

V→max

Здесь смысл чисел отличается от предыдущей задачи. В данном случае,– это доля затрат фирмы на оборудование типаi.

Итак, возможность применения смешанной стратегии реализуется

1. Либо как статистическая или вероятностная смесь. Условием является повторяемость ситуации принятия решений.

2. Либо как физическая смесь. Условием является возможность одновременного использования всех чистых стратегий в некоторых пропорциях.

§ 2.2 Неантагонистические игры

§2.2.1. Понятие неантагонистической игры

Для рассмотренных ранее антагонистических игр характерно, что при любом исходе сумма выигрышей всех участников равна одному и тому же постоянному числу (в частности нулю). В экономике чаще встречается другая ситуация, при которой выигрыш одной стороны совсем необязательно означает проигрыш другой. Например, отношения между работником и работодателем несут в себе конфликт, т.к. эти лица имеют несовпадающие интересы. Тем не менее, существуют варианты, выгодные как работнику, так и работодателю. В частности, если фирма получает выгодный заказ, то это обеспечивает занятость и способствует повышению заработной платы многим работникам. С другой стороны, если фирма разоряется, это невыгодно как работнику, так и работодателю и этот конфликт не является антагонистическим.

Введём формальное описание неантагонистической игры (называемой также игрой с ненулевой или с непротивоположными интересами) двух лиц. Каждый игрок обладает некоторым набором стратегий:

–стратегии первого игрока, где x – его отдельная стратегия;

–стратегии второго игрока, где y – его отдельная стратегия.

Каждая пара называетсяисходом игры. На множестве исходов заданы две функции:

–функция полезности (выигрыш) первого игрока;

–функция полезности (выигрыш) второго игрока.

Частным случаем неантагонистической игры двух участников служит игра, в которой каждый игрок имеет конечное число стратегий. Рассмотренный в §1 пример «Дилемма заключенных» является примером биматричной игры.

В игре с непротивоположными интересами возможны случаи, когда

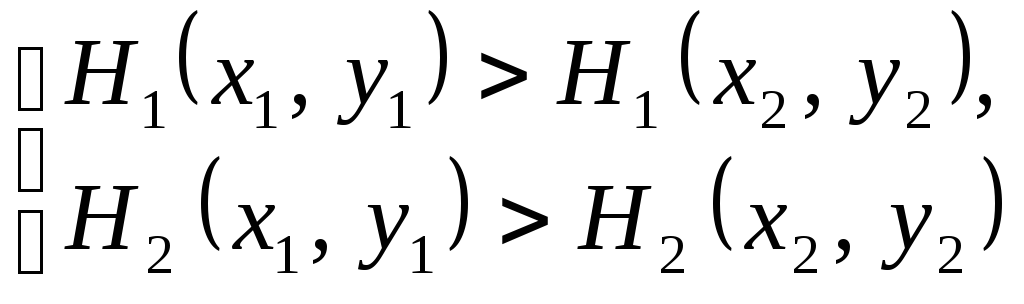(2.1)

В случае (2.1) оба участника исходу предпочитают исход. Если бы участники могли договориться между собой, то они выбрали бы стратегиииВозможно также, что выполняется следующая система

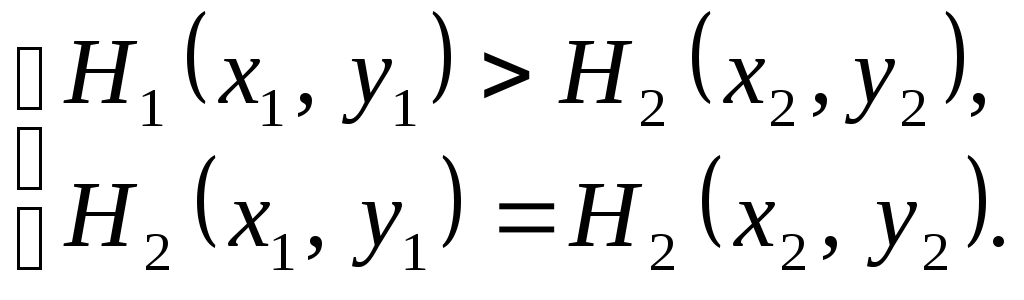(2.2)

В системе (2.2) для первого игрока исход лучше чем, а второму всё равно. Следовательно, возможен компромисс между игроками. В играх с непротивоположными интересами очень важным является вопрос, могут ли участники заключать между собой соглашения, т.е. могут ли они договариваться о совместных действиях. Игры, в которых участники могут заключать между собой соглашения, называютсякооперативными. В противном случае, такие игры называются некооперативными. В этой главе будет рассмотрены только некооперативные игры

Возможны также случаи, когда один из участников выбирает свою стратегию, руководствуясь предполагаемыми действиями другого участника. Таким образом, возникают возможности, которых нет в игре с нулевой суммой:

1. сообщать друг другу о своих намерениях;

2. угрожать партнёру;

3. блефовать (т.е. давать ложные сигналы о своих действиях);

4. накапливать опыт игры;

5. принимать компромиссные решения.

Важно отметить следующее: если в игре с нулевой суммой игрокам было важно скрывать свои намерения, то в играх с нулевой суммой иногда бывает выгодно информировать партнёра о своих действиях. Для иллюстрации рассмотрим два примера.

Пример. «В этой речке утром рано утонули два барана».

Два барана встретились на разных концах мостика, оба хотят быстрее перейти мост. Проблема заключается в том, что каждый из баранов не склонен уступать дорогу другому. У каждого из баранов есть две стратегии: свернуть (уступить дорогу) и не сворачивать. Мостик узкий, если оба не свернут с дороги, то они столкнутся и упадут в речку. Запишем матрицу игры, примерно оценив выигрыши каждого игрока при различных исходах Таблица 1 :

Таблица 1

Найдем равновесные исходы и справедливые исходы.

Решение. Рассмотрим платёжные матрицы для каждого из игроков:

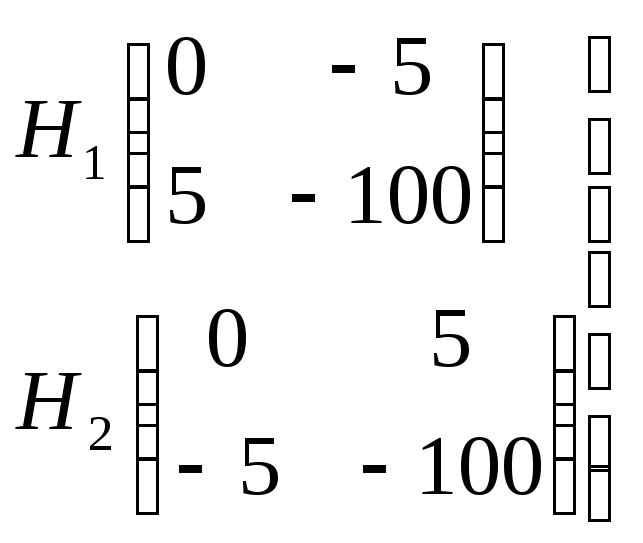– доминирующих стратегий нет.

Если бы участники игры могли бы договориться, они бы исключили ситуацию и приняли единственное справедливое решение(правда, его недостаток в том, что никто не перейдет мост). Возможность для каждого игрока увеличить свой выигрыш, отказываясь от стратегии «не сворачивать», мешает реализации справедливого решения. Исход (0;0) не является равновесным, равновесие наблюдается в исходах (5;-5) и (-5;5), но они не являются справедливыми. Открываются возможности для угрозы, для демонстрации своей решимости перейти мост первым, чтобы второй игрок отступил.

Пример. «Рыночное коварство (блеф)»

Две фирмы выпускают одинаковый продукт, при этом первая фирма занимает доминирующее положение. Фирмы заключили неявный договор – не снижать цены. Если вторая фирма нарушит договор в одностороннем порядке, то первая фирма может ее наказать, например, прибегнув или к экспансии, или к демпингу. У второй фирмы таких возможностей нет. Фирмы могут демонстрировать свои намерения, с помощью рекламы, а также публикаций в СМИ. Так, например, публикация статьи о растущих производственных издержках фирмы служит сигналом о том, что фирма не намерена снижать цену на свою продукцию. Прибыли фирм в зависимости от избранных стратегий – «снижать цену» и «не снижать цену» приведены в Таблице 2. Может ли одна из фирм добиться максимально возможной прибыли?

Таблица 2

Решение.

Легко проверить, что в этой игре нет доминирующих стратегий, нет также равновесных исходов, так как от любого исхода игроки могут отклониться, действуя в своих интересах. Если первая фирма примет стратегию «Не снижать цену», то лучшей стратегией для второй фирмы будет такая же стратегия «Не снижать цену». Но обратное не верно: если вторая фирма примет стратегию «Не снижать цену», то лучшей стратегией первой фирмы будет «Снижать цену». Если первая фирма имеет возможность ввести вторую фирму в заблуждение, подав ей ложный сигнал о том, что собирается не снижать цену, а на самом деле снизит цену, то будет реализован исход с выигрышами (5;0), который дает первой фирме наибольшую прибыль.