Файл: Теория игр для экономистов doc.doc

§2.2.2. Биматричные игры

Частным случаем неантагонистической игры является игра, в которой принимают участие два игрока, каждый из которых имеет конечное число стратегий. Такие игры можно описать с помощью двух матриц, поэтому они называются биматричными.

Пусть первый участник имеет стратегий, а второй –стратегий. Количество исходов равно. Функция выигрышей первого участника может быть задана платёжной матрицейсостоящую из элементов. Аналогично функция выигрышей второго участника будет задаваться матрицейсостоящую из элементовИгру можно также описать с помощью таблицы. В каждой клетке такой таблицы указывается два числа, где первое число – это выигрыш первого участника, а второе число – выигрыш второго.

Рассмотрим пример.

Пример. Игра «Двое в горящем доме». Два человека находятся в горящем доме по разные стороны двери, которую нужно открыть для спасения каждого из них. Для того чтобы дверь открылась, им обоим необходимо приложить общие усилия, заключающиеся в том, что один должен потянуть за ручку двери, а второй, в свою очередь, должен её толкнуть. Запишем эту игры в матричной форме:

Выпишем платёжную матрицу для первого игрока, в которой первая строка доминирует вторую:

В платёжной матрице второго игрока первый столбец доминирует второй:

В этой игре каждому из участников нет необходимости сообщать партнёру о своих намерениях. Если игроки абсолютно рациональны, то каждый из них выберет свою доминирующую стратегию, обеспечивающую наилучший исход для обоих игроков.

§2.2.3. Равновесие Нэша

Рассмотрим неантагонистическую игру двух лиц. с функциями выигрышей иИсход игры будем называтьравновесным, если ни одному из участников не выгодно отклоняться от нёё в одностороннем порядке. Именной такой смысл понятию равновесие придал Джон Нэш. Запишем строгое определение равновесия по Нэшу.

Стратегии иназываютсястратегиями равновесными по Нэшу, если выполняются следующие неравенства:

(2.3)

Таким образом, равновесие Нэша характеризуется тем, что ни одному из участников не выгодно отклоняться от своей равновесной стратегии, если другой участник применяет стратегию, равновесную по Нэшу. Заметим, что это определение сохраняется и для игры с любым числом участников.

Пример. Найти равновесные по Нэшу стратегии в примере 2 (Таблица 1).

Решение. Выпишем все возможные стратегии обоих участников в матрицу и отыщем для каждого из исходов альтернативные исходы, более предпочтительные с точки зрения одного из игроков:

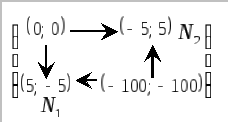
В игре имеется два равновесия по Нэшу. Как правило, равновесие по Нэшу не является единственным.

Существуют игры, в которых нет равновесия в чистых стратегиях. Кроме равновесия в чистых стратегиях случае, может существовать равновесие Нэша в смешанных стратегиях.

Смысл смешанной стратегии для биматричной игры будем определять так же, как и для матричных игр. Смешанная стратегия первого и второго участников есть соответственно вектора X={x₁, x₂,…x_m} и Y={y₁, y₂,…, y_n}, где и(2.4)

Множества смешанных стратегий будем обозначать так же, как множества чистых стратегий – S_x для 1-го игрока и S_y для 2-го.

Функции выигрышей первого и второго игроков при смешанных стратегиях X и Y определяются по формулам

Η₁(x,y)=∑a_ijx_iy_j, Η₂(x,y)=∑b_ijx_iy_j (2.5)

Равновесные по Нэшу смешанные стратегии будем обозначать X^* и Y^* соответственно. Вопрос существования равновесия по Нэшу решается следующей теоремой, доказанной Дж. Нэшем.

Теорема о равновесии по Нэшу. В любой биматричной игре существует, по крайней мере, одно равновесие Нэша. (Без доказательства).

Замечание. Это могут быть равновесия в чистых или смешанных стратегиях.

В общем случае биматричной игры нахождение смешанных равновесий является сложной задачей, но для матриц размера 2x2 решение в смешанных стратегиях найти несложно.

Рассмотрим биматричную игру, в которой каждый игрок имеет две чистые стратегии. Смешанные стратегии игроков будем обозначать x={x₁, x₂} и y={y₁, y₂} соответственно, где 0≤x_i≤1, 0≤y_j≤1, x₁+x₂=1, y₁+y₂=1. Обозначая элементы платежных матриц 1-го и 2-го игроков a_ij и b_ij соответственно, получим Таблицу3 и Таблицу 4 для расчета функций выигрыша.

Таблица3 Таблица 4

Функция выигрыша 1-го игрока будет равна

Η₁(x,y)= x₁(a₁₁ y₁+ a ₁₂ y₂)+ x₂(a ₂₁ y₁+ a ₂₂ y₂),

подставляя x₂=1- x₁ и y₂=1- y₁, получим

Η₁(x,y)= x₁(y₁(a₁₁+ a ₂₂- a ₁₂-a ₂₁)+ a ₁₂-a ₂₂)+ y₁(a ₂₁- a ₂₂)+ a ₂₂.

Обозначим x^*={x₁^*, x₂^*} и y ^*={ y ₁^*, y ₂^*} равновесные по Нэшу стратегии игроков и найдем функцию выигрыша 1-го игрока, при условии, что 2-й игрок применит равновесную по Нэшу стратегию y^*, а 1-й игрок применит произвольную смешанную стратегию x

Η₁(x,y^*)= x₁(y₁^*(a₁₁+ a ₂₂- a ₁₂-a ₂₁)+ a ₁₂-a ₂₂)+ y₁^*(a ₂₁- a ₂₂)+ a ₂₂. (2.6)

Если 2-й игрок применит равновесную по Нэшу стратегию y^*, и 1-й игрок применит равновесную по Нэшу стратегию x^*, то функция выигрыша 1-го игрока будет равна

Η₁(x^*,y^*)= x₁^*(y₁^*(a₁₁+ a ₂₂- a ₁₂-a ₂₁)+ a ₁₂-a ₂₂)+ y₁^*(a ₂₁- a ₂₂)+ a ₂₂. (2.7)

Согласно определению равновесия по Нэшу для всех смешанных стратегий x должно выполняться неравенство

Η₁(x^*,y^*)≥ Η₁(x,y^*). (2.8)

Подставляя в неравенство Η₁(x^*,y^*)- Η₁(x,y^*)≥0 функции из уравнений (4) и (5), получим неравенство

(x₁^*- x₁)( y₁^*(a₁₁+ a ₂₂- a ₁₂-a ₂₁)+ a ₁₂-a ₂₂) ≥0, (2.9)

которое должно выполняться для всех значений x₁ из отрезка [0;1].

Интерес представляет случай, когда равновесная по Нэшу стратегия x^* не совпадает ни с одной чистой стратегией, то есть, когда x₁^* удовлетворяет строгому неравенству 0< x₁^*<1. В этом случае неравенство (2.9) будет верно для всех x₁ из отрезка [0;1] тогда и только тогда, когда

y₁^*(a₁₁+ a ₂₂- a ₁₂-a ₂₁)+ a ₁₂-a ₂₂=0. (2.10)

Уравнение (2.10) дает значение y₁^*, при котором существует смешанная стратегия x^*, не совпадающая с чистыми стратегиями 1-го игрока.

Аналогично, для всех смешанных стратегий y 2-го игрока должно выполняться неравенство

Η₂(x^*,y^*)≥ Η₂(x^*,y) (2.11)

Определяя функции Η₂(x^*,y) и Η₂(x^*,y^*) из таблицы 2, получим условие, при котором 2-й игрок имеет равновесную смешанную стратегию y^*. не совпадающую с его чистыми стратегиями

x ₁^*( b ₁₁+ b ₂₂- b ₁₂- b ₂₁)+ b ₂₁- b ₂₂=0. (2.12)

Если уравнения (2.10) или (2.12) не имеют решений на отрезке [0;1], то в игре существуют только равновесия в чистых стратегиях, существование которых непосредственно следует из неравенств (2.9) и аналогичного неравенства для 2-го игрока.

Пример.Отыскать равновесие Нэша в чистых, либо смешанных стратегиях в игре «орёл-решка».

Таблица 5

Решение. Запишем матрицу игры:

Таблица 6

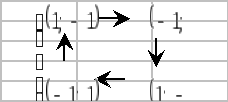
Очевидно, что равновесия по Нэшу в чистых стратегиях не существует. Будем искать решение в смешанных стратегияхx={x₁, x₂} и y={y₁, y₂} соответственно, где 0≤x_i≤1, 0≤y_j≤1, x₁+x₂=1, y₁+y₂=1. Найдем функцию выигрыша 1-го игрока

Η₁(x,y)= x₁y₁- x₁y₂- x₂y₁+ x₂y₂= 4x₁y₁-2 x₁-2y₁+1= x₁(4y₁-2) -2y₁+1.