Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 439

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56



m
( Rk ) некоторого замкнутого контура, при этом они берутся со знаком плюс, если токи совпадают с направлением обхода контура, а в противном случае – со знаком

минус (направление обхода контура выбирается произвольно); Ek–

k1

алгебраическая сумма источников ЭДС, входящих в данный замкнутый контур (берутся со знаком плюс, если направления источников ЭДС совпадают с направлением обхода контура, а в противном случае – берутся со знаком минус).


    1. 1   2   3   4   5   6   7   8   9   10   ...   56

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА



Сложными называются разветвленные электрические цепи с несколькими источниками питания.

Универсальным методом анализа и расчета таких цепей является метод непосредственного применения первого и второго законов Кирхгофа. Однако в сложных цепях сделать это не всегда возможно по причине очень большого числа совместно решаемых уравнений. Поэтому при расчете сложных электрических

цепей используют другие более эффективные методы, базирующиеся на использовании законов Кирхгофа.

      1. Метод суперпозиции (наложения)



Метод основан на принципе независимости действия ЭДС, согласно которому токи, протекающие в цепи при наличии нескольких ЭДС, можно представить как алгебраическую сумму токов, вызываемых каждой из ЭДС в отдельности.

Расчет производится следующим образом:

  1. полагается, что все ЭДС кроме одной, равны нулю;

  2. для данной ЭДС, сохранив неизменными все сопротивления цепи (включая сопротивления источников питания, ЭДС которых приравнена нулю), рассчитываются токи во всех ветвях и отмечаются их направления;

  3. подобный расчет делается столько раз, сколько ЭДС имеется в исследуемой цепи;

  4. действительный ток в каждой из ветвей определяется как сумма найденных частичных токов (при суммировании учитывается направление частичных токов).

Рассмотрим порядок расчета следующей схемы (рис.3.1):


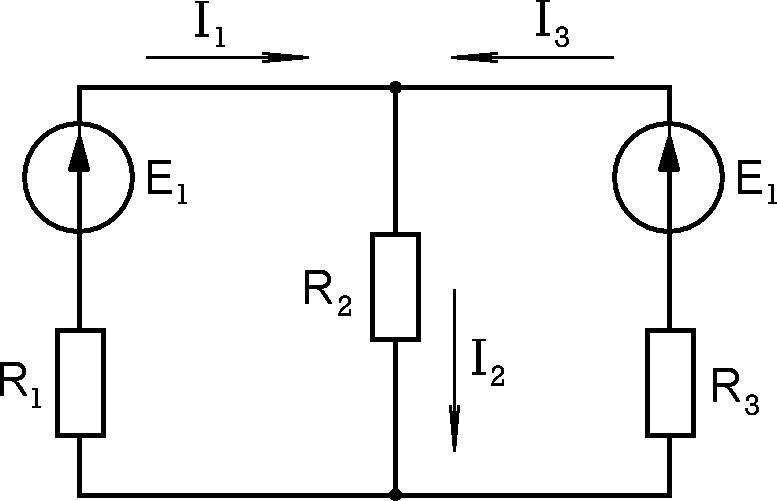
Рис. 3.1
Оставляем только один источник ЭДС, например, ЭДС Е1 (рис.3.2).

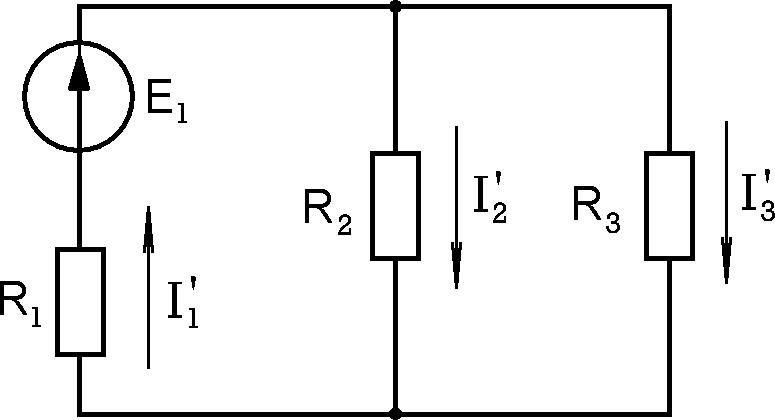
Рассчитываем токи ветвей I , I и

1 2


3
I .

Для этого:


Рис.3.2

а) находим общее сопротивление цепи;

б) находим ток в неразветвленной части цепи;

в) методом разгонки определяем токи в сопротивлениях R2 и R3.


Затем выбираем другой источник ЭДС, а первый приравниваем к нулю (рис.3.3).


2
3
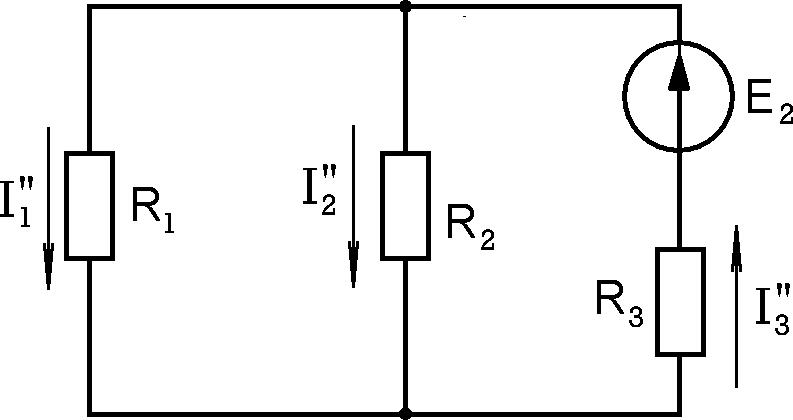 Аналогично предыдущему случаю выполняем расчет частичных


1
токов ветвей I

, I

и I .

Действительные токи ветвей рассчитываются по принципу

суперпозиции

I I I ,

I2 I2 I2 , I3 I3 I3 .

1 1 1



Рис.3.3

За направление действительного тока выбирается направление большего частичного тока.


      1. 1   ...   4   5   6   7   8   9   10   11   ...   56

Метод контурных токов


Используется в сложных цепях с большим числом узлов. Его преимущество перед другими методами расчета в том, что не требуется составлять уравнения по первому закону Кирхгофа, что сокращает общее число совместно решаемых уравнений:

NКТ

Nв Ny1 NT,

где Nв - число ветвей цепи; Ny - число узлов цепи; NT - число ветвей, содержащих только источники тока.

Суть метода контурных токов в следующем.

Электрическая цепь разбивается на N независимых контуров. Предполагается,

что в каждом контуре протекает свой независимый контурный ток

I11 , I22 ,..., Inn.

В том случае, если в цепи присутствуют источники тока, то считается, что в контурах, содержащих источники тока, протекают контурные токи, равные известным значениям данных источников тока. При этом ветвь с источником тока может входить только в один независимый контур (т.е. ветвь с источником тока не может быть общей между независимыми контурами и, таким образом, входить в два или более независимых контура). Для нахождения неизвестных контурных токов записывается следующая система уравнений:

I11 R11 I22 R12 ... Jn Rn E11;

 1



I11 R21 I22 R22  ...  JnRnE22 ;



. . . .
. . . .

2

. . . . .

(3.1)


I


11



Rn1

I22

Rn2

... Jn

n

Rn

Enn,

где

Rnn– собственное сопротивление контура (алгебраическая сумма сопротивлений,

входящих в контур n);

Rnl– общее сопротивление контуров nи l, причём

Rnl Rln;

если направления контурных токов в ветви с данным сопротивлением совпадают, то

Rnl 0

(в противном случае

Rnl 0 );

Rn– общее сопротивление ветви контура “ n” с

контуром, содержащим источник тока

Jn;

Enn – собственная ЭДС контура “ n”

(алгебраическая сумма ЭДС, входящих в контур “ n”).

Решением данной системы уравнений являются контурные токи
I11 , I22 , ..., Inn.

Искомые действительные токи ветвей находятся через найденные контурные токи

методом суперпозиции (если контурные токи, составляющие действительный ток, имеют с ним одинаковое направление, то берутся со знаком плюс, а в противном случае – со знаком минус).

Смотрите также файлы