Файл: Ирина Дмитриевна Сердюкова основы финансовой грамотности энциклопедия эрудита учебное пособие.docx

1

где –––– дисконтный множитель, который показывает,

1 + n•i – во сколько раз первоначальная сумма ссуды меньше наращенной суммы;

Р – приведенная величина, или современная стоимость, будущей суммы;

S – наращенная сумма,

n – период получения дохода (в годах)

i – ставка доходности (в долях).

Рассмотрим следующую задачу:

Какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процента по ставке получить наращенную сумму, равную S?

Пример. Вкладчик банка имеет 333,3 тыс. руб. Какую сумму он будет иметь через на 1 год при условии 50% годовых?

Из формулы (1) получаем:

S = P (1 + i •n)

S =333,3 • (1 + 0,5 • 1) = 333,3 • 1,5 = 500 тыс. руб.

Доход вкладчика в этом случае составит:

D = 500 – 333,3 = 166,7 тыс. руб.

В процессе подготовки к подписанию контрактов возникает необходимость определения срока ссуды. Если согласованы основные параметры ссуды (сумма погашения долга S, процентная ставка i, величина ссуды Р), то срок погашения ссуды можно определить по формуле

_ S–P S: P – 1 ,

п = P i = i

где п – срок ссуды в годах.

2) Банковское дисконтирование

Ранее мы рассмотрели наращение суммы, используя процентную ставку i суммы Р. Однако можно использовать и другой подход, когда за базу (100%) принимается сумма погашения долга. В таком случае применяется учетная ставка d. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды по учетной ставке d.

В таких ситуациях наращенная сумма может быть рассчитана по формуле

S = P , (2)

1 – n•d

где n – срок ссуды;

d – учетная ставка (ставка дисконтирования).

Тогда, первоначальная сумма (текущая стоимость) определяется по формуле P = S (1 – n•d).

Пример. 2. Вексель номинальной стоимостью 500 тыс. руб. переуступается банку. Время до погашения векселя 2 месяца. Какую сумму получит векселедержатель если банк принимает его по учетной ставке 50% годовых.?

Решение: Обозначим через S – номинал векселя, то есть эту сумму получить банк у должника. Тогда P – текущая стоимость векселя (цена покупки векселя банком). Теперь переведём месяцы в годы: 2 мес. / 12 мес. = 0,166. Теперь воспользуемся формулой (2), преобразовав её:

P =

S (1 -nd)..

От сюда, P = 500 • (1 – 0,166 • 0,5) = 458,5 тыс. руб.

Дисконт (доход банка) в этом случае составит:

D = 500 – 458,5 = 41,5 тыс. руб.

Ставки, применяемые в математическом и банковском учетах, решают практически одни и те же задачи – определение величины Р по заданной F. Это позволяет установить связь между ними, выразив одну ставку через другую. Определим связь между процентной и учетной ставками, для чего запишем формулы расчета современной величины платежа при математическом и банковском видах учета:

Взаимосвязь ставок:

• Процентная ставка (математическое дисконтирование)

i_t= S–P

P

• Учетная ставка (банковское дисконтирование)

d_t=S–P

S

• Соотношение между ставками

i_t = d_t или d_t = i_{t ,}

1 – d_t1+i_t
Эти выражения позволяют определить процентную ставку по известной учетной ставке (первое выражение) или учетную ставку по известной процентной ставке. Таким путем мы получаем различные по величине процентные ставки, которые дают одну и ту же дисконтированную величину платежа при фиксированном сроке ссуды. Такие ставки называют эквивалентными. Они используются при сравнении доходности сделок.

1а) Дисконтирование по сложной ставке процента

Расчеты по сложным процентам используются при долгосрочных финансовых операциях. Они основаны на условии, что начисленные за период проценты присоединяются к первоначальной сумме, а определение суммы процентов за следующий период производится исходя из наращенной к началу периода суммы. Таким образом, исходная база начисления в каждом периоде увеличивается на сумму присоединившихся процентов. Процесс наращения происходит здесь с ускорением. Учет по сложным процентам, как и по простым, заключается в определении первоначальной суммы (Р) по заданным наращенной сумме, процентной ставке и периоде сделки по следующей формуле:

1

Р = S –––, (1a)

(1 + i) ⁿ

1

где –––– дисконтный множитель

(1 + i) ⁿ

Если начисление процентов производится несколько раз в течение года, то расчет современной величины платежа необходимо производить по формуле

S

Р = –––––– ,

(1 + i)^nm

^m

где т – число случаев начисления процентов в течение года.

Пример. Определим размер вклада, если вкладчик через 5 лет хочет получить 200 млн руб. Банк предлагает производит начисления на внесенную сумму по сложной ставке 20% годовых.

200

Р = ––– = 80,375 млн руб.

(1 + 0,2)⁵

Если начисление процентов производится ежеквартально, то первоначальная сумма вклада будет меньше.

200

Р = –––––– =75,378 млн руб.

(1 + 0,2 )⁴•⁵

⁴

2а) При банковском (коммерческом) дисконтировании по сложным учетным ставкам используется формула:

P = S (1 – d)ⁿ. (2а)

Пример. Определим величину банковского кредита сроком 5 лет, если всего банк желает получить в результате сделки 200 млн руб. при рентабельности сделки для банка 20% годовых по сложной ставке.

Р = 200 (1 – 0,2)⁵=65,536 млн руб.

8.4.2. СФЕРЫ ПРИМЕНЕНИЯ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ

Финансовые вычисления используются для решения широкого круга задач: от простейших расчетов по начислению простых и сложных процентов, определению эквивалентности процентных ставок и до количественного анализа потоков платежей, эквивалентного изменениям параметров финансовых сделок, ранжирования вариантов инвестиций, разработки планов погашения долгосрочных кредитов и займов, оценке финансовой эффективности различных кредитных и коммерческих операций.

8.4.2.1. Ежемесячное погашение кредита при использовании метода аннуитета

Смысл в том, что взята некая сумма на некоторый срок, которая погашается равными ежемесячными частями. При этом, ставка процента применяется только к основной сумме долга, которая в свою очередь постоянно уменьшается. Это принцип доливаемого стакана. В средневековой Европе был следующий метод застолья, при котором алкоголя организм получал мало, но общий объем выпитого был достаточно большой. За столом 10 человек (отец семейства, его 6 сыновей, 3 гостя) и 2-х литровый кувшин алкогольного напитка. Застолье продолжается полтора часа. За это время произносят 5 тостов. Каждый раз мужчины пьют из полного стакана. 1-й тост – выпивается пол стакана. И после этого каждый разбавляет свой стакан водой. 2-й тост – аналогично.

Ежемесячный платеж по кредиту содержит плату за пользование кредитом и частичное погашение суммы основного долга.

Вот и получается, что заёмщик в первый месяц платит самые большие проценты – на основную сумму долга, а уже во 2-й месяц процентов будет меньше.

Базовая формула:

P

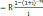
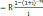
Текущая стоимость аннуитета.

P = R *[{1 – (1+i)^-n}/i]

P = R *[{1 – (1+i)^-n}/i]

при однократном начислении процентов в год, тогда при многократном начислении процентов в год нужна формула:

P = R *[{1 – (1+i/m)^-n*m}/(i/m)],

где P – текущая (первоначальная) сумма долга. То есть просто размер кредита.

i – годовая ставка процента в долях.

i = I% /100%,

где I – годовая ставка процента в математических процентах.

n – количество периодов начислений, в годах.

m – количество начислений в год.

R – размер единичного платежа/взноса в счет погашения долга и выплаты процентов.

R = S / n при однократном начислении процентов в год и R = S / (n * m).

где S – будущая стоимость долга.

То есть сколько всего предстоит вернуть с учетом процентов. S = R * n при однократном начислении процентов в год и S = R * n * m.

а) Определение текущей и будущей стоимости ренты

Рента – это серия периодически осуществляемых платежей. Примером потоков с платежами произвольной величины могут служить выплаты дивидендов по обыкновенным акциям, капиталовложения в долгосрочные активы и т.д. Расчет характеристик таких потоков представляет собой определенные вычислительные трудности. В финансовых расчетах обычно возникает вопрос определения обобщающих характеристик – наращенной суммы ренты и современной величины ренты. Наращенная сумма ренты представляет сумму всех периодических платежей с начисленными на них процентами к концу ее срока. Современная величина ренты – это сумма всех периодических платежей, дисконтированных на начало срока ренты.

Если рента состоит из платежей одинакового размера и они осуществляются через одинаковые промежутки времени, то количество денег, которое может быть инвестировано в ренту, определяется по формуле текущей стоимости ренты (постнумерандо):

PV = Rс+Rс +…..+ Rс , (1)

(1+ i) (1+ i)².... (1+ i)ⁿ

или:

PV = ∑ Rс ,

(1+ i)ⁿ

или:

PV = Rс

– 1• Rс , (1а)

i (1+ i)ⁿi

где PV – текущая стоимость ренты;

Rс – ежегодные выплаты равными суммами; (член ренты)

i – процентная ставка (коэффициент окупаемости капиталовложений, предпочтительный для инвестора).

Пример. Компания сдает в аренду имущество сроком на 5 лет, арендная плата составляет 50 млн руб. в год, определен барьерный коэффициент рентабельности в 20%. Следовательно, общая сумма платежей за 5 лет составит 250 млн руб. Текущая стоимость арендной платы cоставит:

PV = 50 – 1 • 50 = 149,5 млн.руб.

0,2 (1+ 0,2)⁵0,2

Для расчета будущей стоимости обыкновенной ренты (постнумерандо) применяется формула:

FV = R ∑ (1+ i)ⁿ, (2)

или

FV = R • (1+ i)ⁿ– 1 , или: FV = R • (1+ i)ⁿ– R , (2а)

iii

где FV – будущая стоимость аннуитета;

R – ежегодные вклады равными суммами; (член ренты)

i – процентная ставка (коэффициент наращивания капиталовложений, предпочтительный для инвестора).

Подобные расчеты в страховании называют актуарными. Они позволяют рассчитать объем потоков денежных средств, накопленную сумму страхового фонда и т.д.

Пример. Для погашения пакета облигаций, выпущенных на 5 лет, создается погасительный фонд при ежегодных платежах по 20 млн руб., на которые начисляются проценты по ставке 10%. Определим итоговую (наращенную) сумму при условии, что проценты начисляются один раз в год.

FV = 20 • (1 +0,l)⁵ – 20 =1,61051х200-200= 122,102 млн руб.

0.10.1

Таким образом, по истечении 5 лет предприятие накопит 122,1 млн руб. для погашения пакета выпущенных облигаций.

б) Расчет текущей стоимости и доходности ценных бумаг

Напомним, что стоимость ценной бумаги это абсолютная величина. Различают: номинальную и рыночную стоимость.

Доходность – это относительная величина: в общем виде это отношение дохода от данного финансового актива к объему инвестиций. Различают купонную и текущую доходность, доходность к сроку погашения.

Текущая рыночная стоимость любой ценной бумаги в общем виде может быть рассчитана по следующей формуле: