Файл: Теория игр для экономистов doc.doc

Для равновесных по Нэшу стратегий x^*={x₁^*, x₂^*} и y^*={ y ₁^*, y ₂^*} найдем значение функции выигрыша будет равно

Η₁(x^*,y^*)= x₁^*(4y₁^*-2) -2y₁^*+1

Если 2-й игрок применит равновесную по Нэшу стратегию y^*, а 1-й игрок произвольную смешанную стратегию x, то функция выигрыша 1-го игрока составит значение

Η₁(x,y^*)= x₁ (4y₁^*-2) -2y₁^*+1.

Из условия равновесия Η₁(x^*,y^*)≥ Η₁(x,y^*) следует неравенство

(x₁^*- x₁) (4y₁^*-2) ≥0

для всех x₁ из отрезка [0;1]. Поскольку в игре нет равновесия в чистых стратегиях, то x₁^*≠0 и x₁^*≠1, то множитель (x₁^*- x₁) может быть и положительным и отрицательным в зависимости от x₁. Следовательно, последнее неравенство выполняется лишь при условии, что второй множитель равен нулю, то есть 4y₁^*-2=0. Откуда находим y ₁^*=0,5 и y ₂^*=0,5.

Аналогично находим равновесную по Нэшу стратегию 1-го игрока x₁^*= x₂^*=0,5. Значения игры для 1-го и 2-го игроков равны Η₁(x^*,y^*)= Η₂(x^*,y^*)=0,5.

Пример. «Семейный спор». Муж и жена собираются провести вместе выходной день. Муж предпочитает пойти на футбол, а жена на балет. Выигрыши мужа и жены в зависимости от принятых стратегий приведены в таблице:

Таблица 7

Решение. Выпишем общую матрицу игры.

В этой игре существует два равновесия Нэша в чистых стратегиях. Кроме того, можно показать, что существует равновесие Нэша и в смешанных стратегиях. Для этого найдем платежную функцию 1-го игрока (мужа) для смешанных стратегий x={x₁, x₂} и y={y₁, y₂}.

Η₁(x,y)=2x₁y₁+0,5 x₁y₂+x₂y₂=1,5 x₁y₁-0,5 x₁+ y₁-1= x₁(2,5 y₁-0,5) +1- y₁.

Соответственно получаем

Η₁(x^*,y^*)- Η₁(x,y^*)=(x₁^*- x₁) (2,5y₁^*-0,5).

Неравенство Η₁(x^*,y^*)≥ Η₁(x,y^*) будет верно для всех x₁ из отрезка [0;1] и 0< x₁^*<1, если 2,5y₁^*-0,5=0, откуда y ₁^*=1/5 и y ₂^*=4/5.

Аналогично, для 2-го игрока (жены) получаем платежную функцию

Η₂(x,y)= x₁y₁+0,5 x₁y₂+2x₂y₂=2,5x₁y₁-2y₁-1,5x₁+2.

Тогда Η₂(x^*,y^*)- Η₂(x^*,y)=( y₁^*- y₁) (2,5 x ₁^*-2).

Неравенство Η₂(x^*,y^*)≥Η₂(x^*,y) будет верно для равновесной смешанной стратегии y^*={y₁^*,y₂^*} и произвольной стратегии y={y₁, y₂} при условии, что 2,5x₁^*-2=0, откуда находим x₁^*=4/5, x₂^*=1/5 (муж выбирает футбол с вероятностью 4/5 и балет с вероятностью 1/5).

Аналогично находим y ₁^*=1/5, y ₂^*=4/5. Функции выигрыш игроков в смешанном равновесии будут равны Η₁(x^*,y^*)= Η₂(x^*,y^*)=4/5.

§2.2.4. Эффективность по Парето2

Если интересы игроков не противоположны, то в игре могут существовать исходы, один из которых предпочтительнее других с точки зрения всех игроков. Рассмотрим уже известный пример «Дилемма заключенных».

Пример. «Дилемма заключённых» (см §1.1).

Таблица 8

Решение. Выпишем матрицу игры и найдём равновесие по Нэшу.

Таблица 9

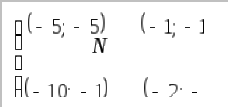
Равновесный по Нэшу исход (-5; -5) является менее выгодным для обоих участников, чем (-2; -2). Если бы игроки могли договориться, то они отказались бы от своих равновесных стратегий, чтобы перейти к более эффективному для каждого из них исходу (-2;-2).

Принцип эффективности по Парето позволяет сравнивать исходы игры попарно, пользуясь следующим определением.

Исход 1 называют более эффективным по Парето исходом, чем исход 2, если, переходя от исхода 2 к исходу 1, увеличивается выигрыш хотя бы одного игрока, а выигрыши других игроков, по крайней мере, не уменьшаются.В этом случае говорят, что исход 1 доминирует по Парето исход 2.

В биматричной игре доминирование по Парето исхода (l;k) над исходом (p;q) означает, что - либо верны неравенства a_lk> a_pq и b_lk≥ b_pq, либо верны неравенства b_lk> b_pq и a_lk≥ a_pq.

Если в игре существует исход, который доминирует по Парето все остальные исходы, то его называют Парето-оптимальным исходом. Легко проверить, что Парето-оптимальный исход, если он существует, является равновесным по Нэшу.

В рассмотренных выше примерах нет Парето-оптимальных исходов, но есть исходы, доминируемые по Парето всеми другими исходами. Например, в игре «Семейный спор» это исход (0;0).

Исходы, равновесные по Нэшу, могут быть не эффективными по Парето, и наоборот, что мы видим в примере «Дилемма заключенных». Наличие в игре Парето-оптимального исхода, или наличие исхода, доминируемого по Парето всеми другими исходами, создают предпосылки для выработки игроками совместных решений, то есть для создания коалиций. Однако, даже в случае бескоалиционной игры, игроки, как мы покажем в следующей лекции, имеют возможности избежать невыгодных для всех исходов.

§2.2.5. Повторяющиеся игры. Применение к микроэкономике.

Пусть одни и те же условия игры с теми же игроками воспроизводятся многократно. В таком случае мы имеем расширение игры, которое называют повторяющейся игрой. Нетрудно заметить, что в повторяющейся игре смешанные стратегии могут применяться как частоты использования чистых стратегий. Возможность использования смешанных стратегий не является единственным преимуществом повторяющейся игры.

При повторении одной и той же игровой ситуации (при многократном разыгрывании игры) изменяются мотивы рационального поведения участников игры: во-первых, каждый из участников получает представление о предпочтениях другого участника; во-вторых, каждый участник, выбирая свою стратегию на некотором n-м шаге, даёт ответ на выбор другого участника на шаге. В игре возникают коммуникации между участниками. Подавая сигнал в виде выбранной на очередном шаге стратегии, этого, участник может влиять на выбор стратегии партнером на следующем шаге. Таким образом, в повторяющейся игре возникают предпосылки к совместному выбору стратегий, т.е.кооперации. Однако, существование этих предпосылок совсем не гарантирует того, что участники игры смогут кооперироваться.

Эти обстоятельства имеют большое значение при анализе рынков с олигополистической конкуренцией (дуополия). Рассмотрим пример.

Пример. «Назначение цены». Две фирмы, выпускающие однотипный продукт, конкурируют друг с другом, устанавливая различные цены на свою продукцию. Выпуски фирм считаем заданными и неизменными. Такая конкуренция двух дуополистов называется ценовой конкуренцией или конкуренцию по Бертрану³.

Для простоты будем считать, что каждая фирма выбирает одну из двух стратегий: низкая цена, высокая цена. Будем также считать, что фирмы назначают цену в начале каждого месяца независимо друг от друга. Так как продукт фирм однотипен, то потребитель будет осуществлять выбор, исходя только из цены. Та фирма, которая назначит более высокую цену, понесет убытки. С другой стороны, более высокая цена даст большую прибыль при условии, что на продукцию фирмы будет спрос. Прибыли фирм для каждого из возможных исходов приведем в таблице 9.

Таблица 9

Решение. Выпишем матрицу игры и найдём равновесие по Нэшу.

Таблица 10

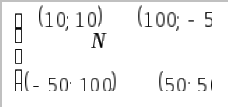
Равновесным по Нэшу исходом будет (10;10), а равновесными стратегиями – назначение низкой цены. Таким образом, дуополия Бертрана дает тот же эффект, что и совершенная конкуренция – снижение цены до уровня предельных издержек. Что мешает фирмам принять наиболее эффективную для них стратегию высоких цен с выигрышами? Исход (50;50) не является равновесным по Нэшу, поэтому, даже если фирмы договорятся об установлении высокой цены, каждой фирме в отдельности будет выгодно снижать цену. Ценовый сговор запрещён антимонопольным законодательством, но дуополия Бертрана показывает, что препятствием для сговора служит конкуренция. «Сговор разрушается зубилом конкуренции»э

Известны, однако, практические примеры, что олигополии воздерживаются от снижения цены в течение длительного времени. Следовательно, у фирм в условиях олигополии есть возможность координации действий. Как осуществляется эта координация, и может ли возникать исход, равновесный по Нэшу и эффективный по Парето?