Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Трансформатор – устройство, передающее энергию из одной цепи в другую посредством электромагнитной индукции. У воздушного трансформатора отсутствует сердечник. Применяется в высокочастотных цепях (на частотах, превышающих 20 кГц).

Обмотка, к которой подводится напряжение питания, называется первичной (ПО), а обмотка, подключаемая к нагрузке называется вторичной (ВО).

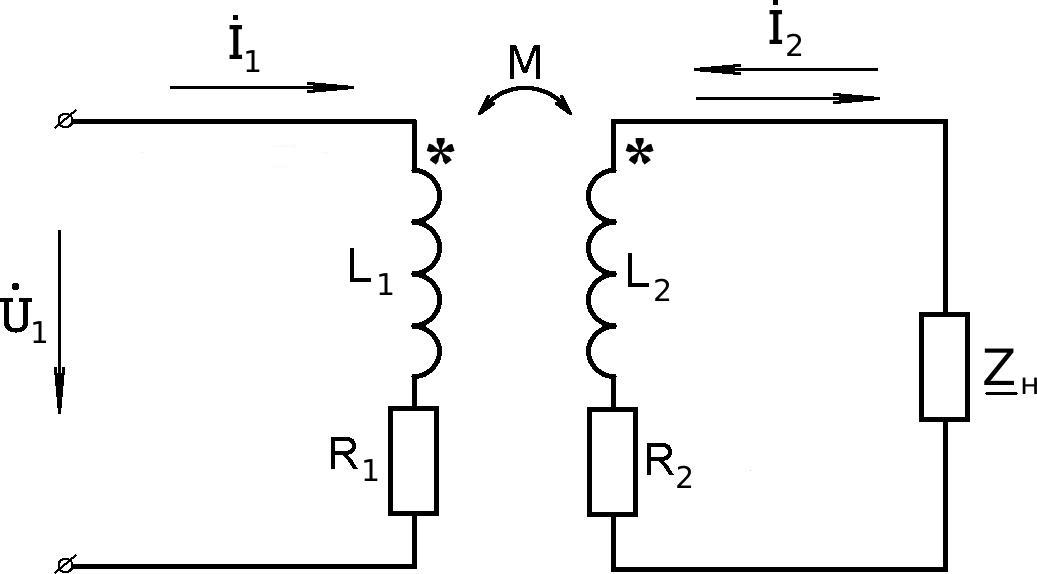
На рис. 6.9 показана схема трансформатора.

R₁и

R₂– активные

сопротивления обмоток, L₁ и L₂ – индуктивности первичной (ПО) и вторичной (ВО) обмоток соответственно.

Определим входное сопротивление данного трансформатора Z_вх. Очевидно, что при отсутствии ВО

1
Z_вх R₁ j ω L. (6.5)

Получим выражение для
^Zвх

Рис.6.9

с учетом взаимной индуктивной связи между ПО

и ВО. По второму закону Кирхгофа для двух независимых гальванически, но индуктивно связанных контуров запишем уравнения

^U^₁ (R₁



j ω L₁)  I^

 j ω M I^;

(6.6)

2

1
_0  (R₂

j ω L₂ Z_H)  I^

 j ω M I^.

1

2
Формула для определения входного сопротивления имеет вид:

^Zвх

 ^U^¹.

I


1

I

2
Выразим из второго уравнения системы (6.6) ток ^

1

2
I^

 j ω M I^

R₂ j ω L₂ Z_H

и подставим его в первое уравнение системы (6.6), получим

U^ (R j ω L)  I^

 j ω M

 j ω M I^_

2

1
1 1 1 1

R j ω L₂ Z_H

2

2
 (R j ω L)  I^

(ω M)²

 I^.

1 1 1

R j ω L

Окончательно:

^Zвх



_U

 R

I
1 _

_1

1

j ω L

R

(ω M)²

1
.

2
j ω L Z_H

(6.7)

2

1
При сравнении (6.7) и (6.5) видим, что третье слагаемое – комплексное сопротивление, вносимое из вторичной цепи в первичную. Вносимое сопротивление– это такое сопротивление, которое следовало бы "внести" в

первичную цепь (включить последовательно с

L₁и

R₁), чтобы учесть влияние

нагрузки вторичной цепи трансформатора на ток в его первичной цепи.

Тогда эквивалентная схема для определения входного сопротивления воздушного трансформатора будет иметь вид (рис.6.10):

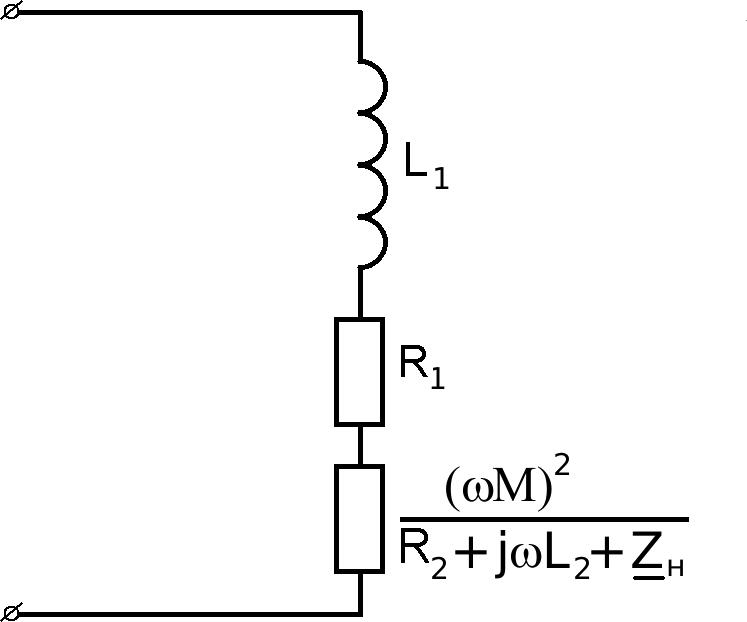
Рис.6.10

1 ... 32 33 34 35 36 37 38 39 ... 56

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

системы ЭДС
Трехфазная цепь строится на основе трехфазных синхронных генераторов, генерирующих совокупность трех ЭДС, одинаковых по частоте и амплитуде, но сдвинутых друг относительно друга на угол 120°. Упрощенная схема трехфазного синхронного генератора показана на рис.7.1.

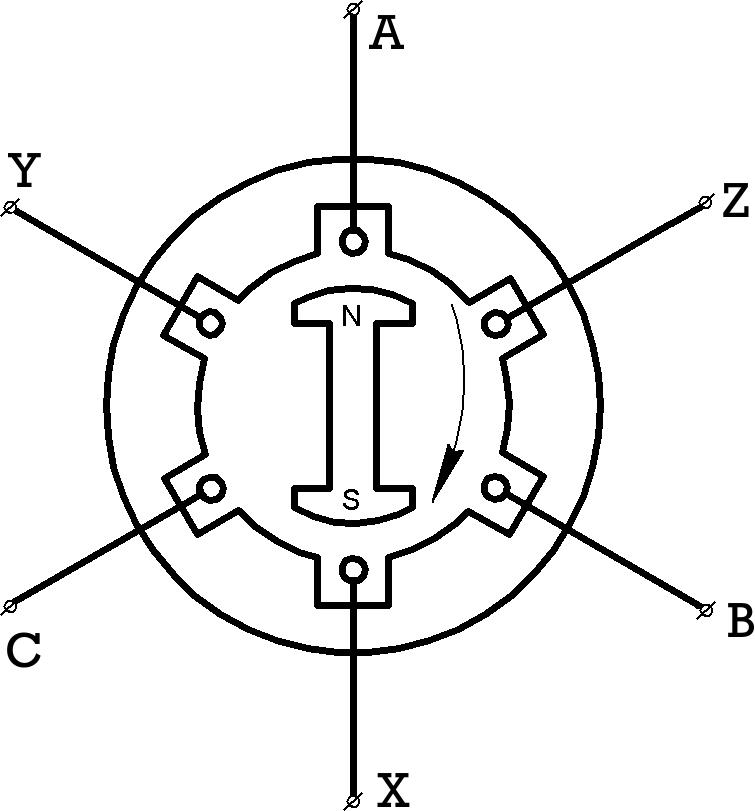
Рис.7.1
Вся обмотка статора состоит из трех частей (фаз). Обмотки фаз

пространственно сдвинуты на статоре на угол

2π3

(таким образом,

2π3

– угол

между магнитными осями фазных обмоток). Условно каждая фазная обмотка

представлена всего одним проводником (витком). Начала обмоток обозначены буквами A, B, C, а концы – X, Y, Z.

ЭДС в витках статора наводится за счет того, что магнитное поле вращающегося ротора пересекает эти витки и наводит в них ЭДС индукции. Частота этих ЭДС будет одинаковой, а по фазе они, в силу пространственного смещения обмоток, отличаются друг от друга.

Трехфазные системы, в фазных обмотках которых наводятся ЭДС одинаковые по амплитуде, но сдвинутые относительно друг друга по фазе на

угол

2π

3

,называютсясимметричными.




По определению симметричной трехфазной цепи имеем:

e E sin ω t; e E sin^ω t ²^^π^;

e E sin^ω t ²^^π^.


AmBm^



₃ _C_m ₃

В комплексной форме действующие значения фазных ЭДС перепишутся в

виде:

_E _A

 E e^j^⁰^;

_E _B

 E e

__j_2π

3 _;

_E_C

 E e

_j_2π

3

Графическое изображение представлено на рис.7.2.

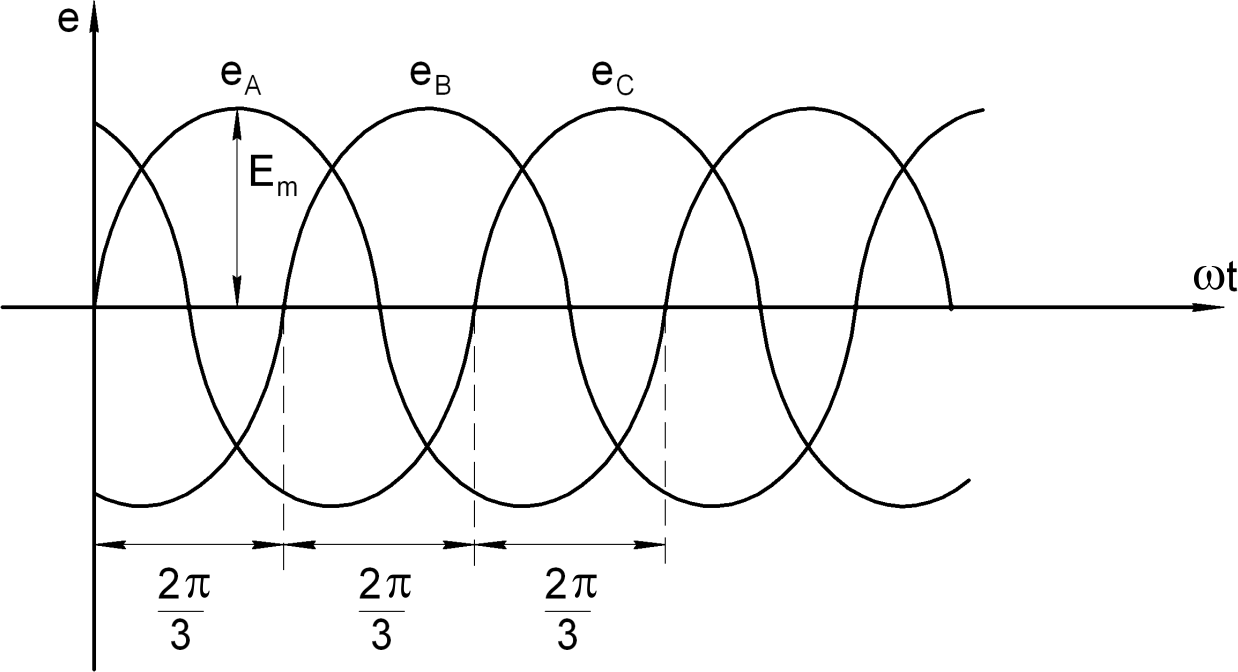
Рис.7.2

Векторная диаграмма для прямой последовательности фаз, когда ЭДС

_E _A

опережает ЭДС

E^_B, а

_E _B

соответственно опережает

_E_C

показана на рис.8.3. Такая

последовательность чередования фаз называется прямой. Она наиболее часто используется на практике.

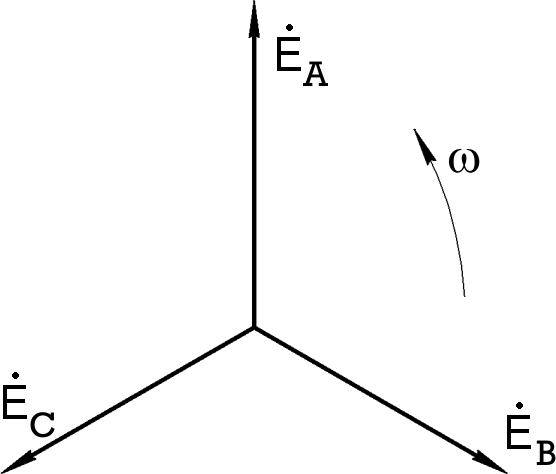
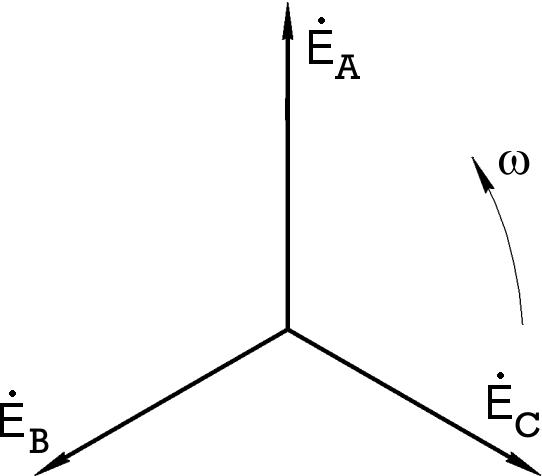
^Рис.7.3Рис.7.4
Обратная последовательность чередования фаз изображена на рис.7.4.

Очевидно, что:

E^_A E^_B E^_C

 0 .

Преимущества трехфазных цепей:

по сравнению с однофазными системами более экономичны при производстве и передаче энергии на расстояние;
возможность простого получения вращающегося магнитного поля, необходимого для работы трехфазных машин переменного тока;
возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.