Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 437
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
Ldiсв
dt
-
iсв
R 0 . (8.5)
Решением данного дифференциального уравнения является выражение:
iсв A ept,
где A– постоянная интегрирования; р– корень характеристического уравнения.
Как уже отмечалось выше (в п.8.1), постоянные интегрирования определяются из граничных условий, задаваемых законами коммутации.
В данном случае постоянная интегрирования A определяется из следующего граничного условия, записанного на основе первого закона коммутации
(iпр iсв) |t0 i|t0 0 .
Отсюда:
iсвt0
iпр
U.
R
С другой стороны
iсв
|t0
A ep0 A.
Следовательно,
A U.
R
Корень pопределяется из характеристического уравнения, записываемого по
виду уравнения (8.5)
p L R 0 . Откуда
p R. В результате ток
L
iсвравен:
iсв
U
R
Rt
eL
U
R
t
eτ,
где
τ L 1
– постоянная времени цепи, определяющая скорость протекания
Rp
переходного процесса. Теоретически переходный процесс длится бесконечно долго. Однако принято считать, что он закончился, если ток iсоставляет 99% от
установившегося значения
I U
R
. Это имеет место при
t (3 4) τ.
Искомый ток равен
i iпр
-
iсв
U U RR
-
t
eτ
U 1 e R
t
τ .
Временная диаграмма процесса включения цепи с R и L на постоянное напряжение изображена на рис.8.2.
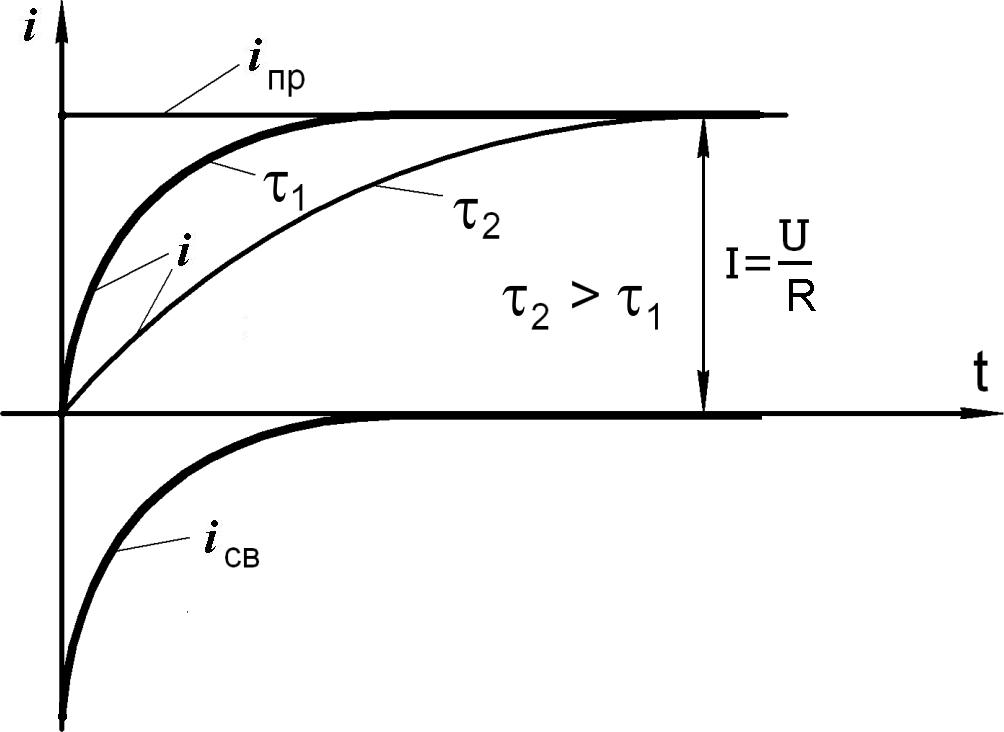
Рис.8.2
На этом же рисунке показаны два графика изменения тока в цепи в зависимости от постоянной времени . Видно, что чем больше значение L, при неизменном сопротивлении R, тем больше энергия магнитного поля, накапливаемая
L i2
в магнитном поле катушки W , и тем больше постоянная времени цепи .
2
- 1 ... 42 43 44 45 46 47 48 49 ... 56
Короткое замыкание RL цепи постоянного тока
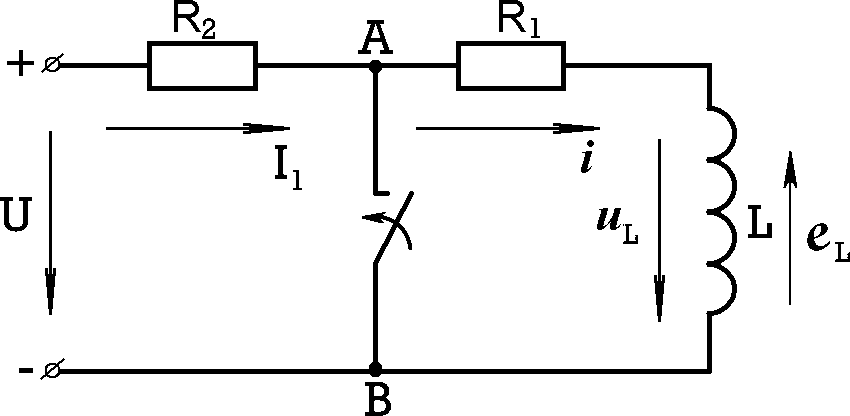 Если ключ на рис.8.3 не замкнут, то через некоторое время в
Если ключ на рис.8.3 не замкнут, то через некоторое время вцепи установится ток
I1
U,
R1 R2
Рис.8.3
определяемый напряжением источника и активным сопротивлением цепи.
При замыкании ключа в момент времени t = 0 напряжение на участке AB равно нулю.
L I2
Запас энергии магнитного поля
1
и ток iначинают исчезать, но не
2
скачком, а постепенно, т.к. при изменении тока в замкнутой цепи на катушке L наводится ЭДС самоиндукции, поддерживающая ток i. Энергия магнитного поля преобразуется в тепловую энергию на сопротивлении R1, которая выделяется в окружающее пространство.
Для замкнутого контура с катушкой второй закон Кирхгофа имеет вид:
1
L
u i R 0 ;
Ldi i R
0 . (8.6)
dt 1
Очевидно, что
iпр|t 0 , и, следовательно,
i iсв iпр iсв.
Уравнение (8.6) примет вид:
Ldiсв
dt
-
R1
iсв
0 .
Решением данного уравнения является
R1 t
iсв
A ept
A eL.
Постоянную интегрирования A определим из первого закона коммутации:
iñâ
|t0
i|
t0
U
R1 R2
-
это с одной стороны;
iсвt0
A ep0 A
-
с другой стороны.
Следовательно,
A U.
R1 R2
Окончательно,
 i iсв
i iсв U
R1 R2
-
R1 t
eL
I1
-
t
eτ,
где τ
1
p
L.
R1
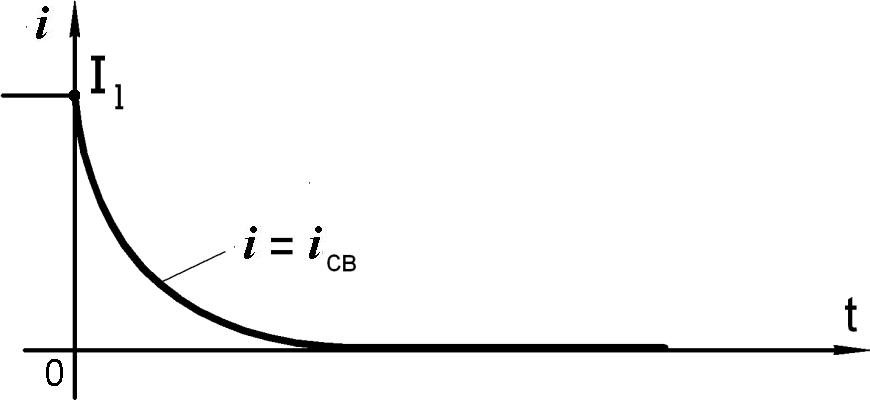
Рис.8.4
Временная диаграмма для данного процесса показана на рис.8.4.
- 1 ... 43 44 45 46 47 48 49 50 ... 56