Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

U E₀  I R_.

Следовательно, пока нелинейный элемент находится под напряжением, не выходящим за пределы линейного участка вольт-амперной характеристики (U_a U U_), его можно заменить эквивалентной линейной схемой (рис.4.6).

Если характеристика нелинейного элемента наклонена в сторону оси напряжения (рис.4.7), то прямая, продолженная от начала линейного участка характеристики, отсечет на отрицательной части оси напряжения участок в

масштабе равный

E₀.

Аналогичные рассуждения позволяют записать:

откуда

R_

U E₀  I R_.

_U

I

 m^dc m

R_bcR

 tgα ^U^^E⁰,

I

Эквивалентная схема нелинейного элемента изображена на рис.4.8.

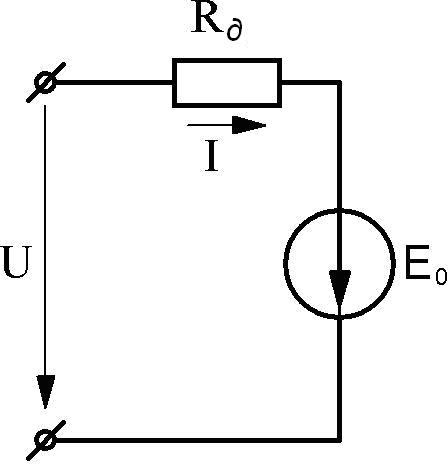
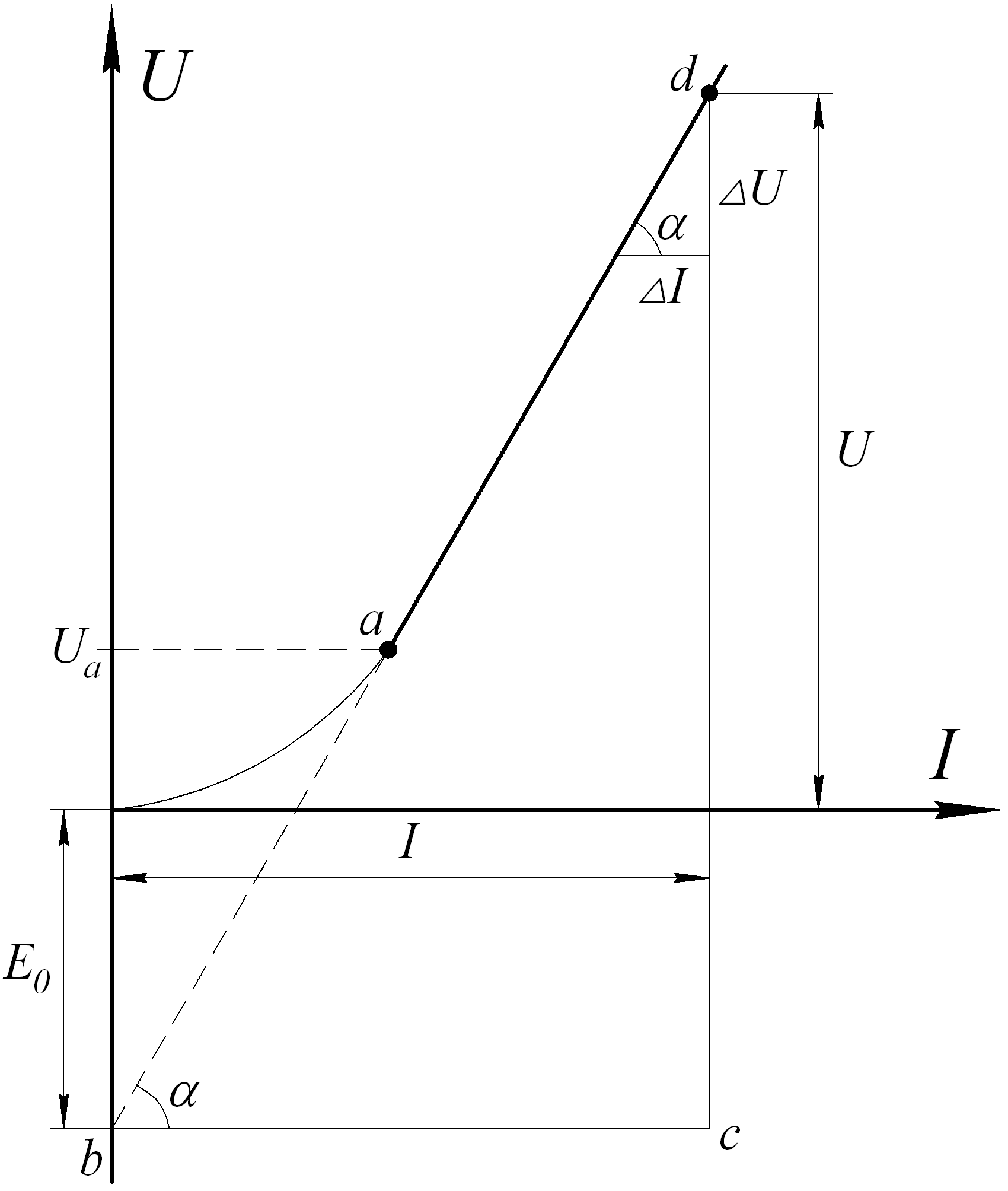_Рис.4.7Рис.4.8

Как отмечалось выше, подобные замены можно осуществлять только в том случае, если изменения напряжения на нелинейном элементе происходят в пределах линейного участка его характеристики.

1 ... 11 12 13 14 15 16 17 18 ... 56

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Основные понятия

Современная электроэнергетика базируется на передаче энергии на большие расстояния при помощи электрического тока. С целью уменьшения потерь для этого нужно сначала ток большой силы и малого напряжения преобразовать в ток малой силы и большого напряжения, а затем на приеме произвести обратное преобразование. Это с высоким КПД и с малыми потерями позволяют сделать трансформаторы. В связи с тем, что трансформатор является устройством переменного тока, вся современная электроэнергетика построена на применении переменного тока. В этом, в частности, состоит и актуальность изучения данного вопроса.

Выше уже отмечалось, что электромагнитный процесс в цепи, при котором значения токов и напряжений повторяются через равные промежутки времени, называется периодическим.

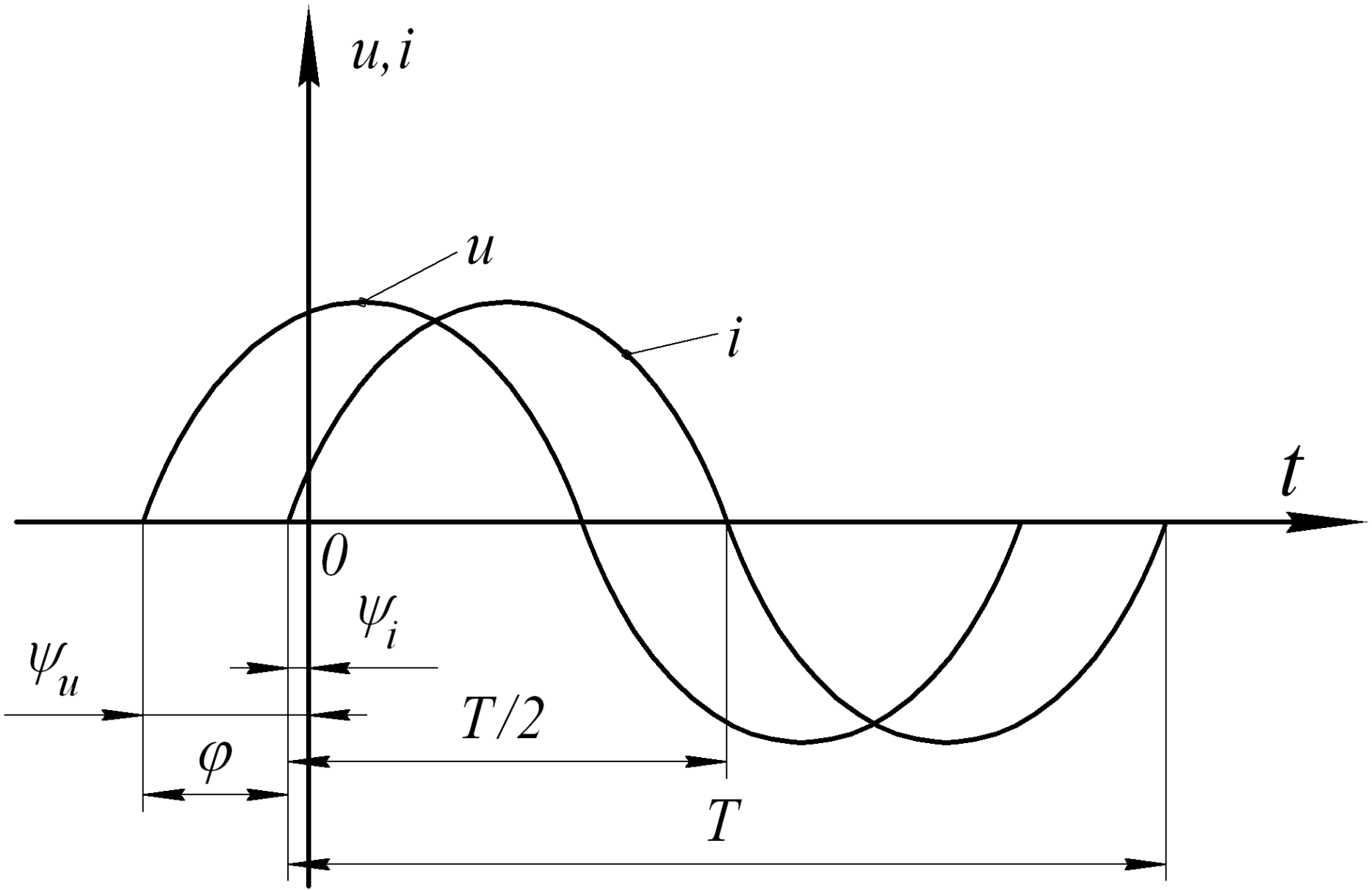Примером простейшего периодического процесса является гармонический процесс (рис.5.1) изменения напряжения, тока и ЭДС в цепи, описываемый уравнениями:

m
i I sin(ω tψ) ,

i

m

m
u U e  E

 sin(ω tψ

 sin(ω tψ

_u) , (5.1)

_e) .

Рис.5.1

Здесь

I_m– амплитудное значение тока,

U_m– амплитудное значение напряжения, E_m– амплитудное значение ЭДС.

Амплитудным значением синусоидальной функции называется наибольшее значение ее мгновенной величины.

Значения аргументов синусоидальных функций (ω t φ) называются фазами синусоид. Фаза характеризует численные значения описываемой величины в данный момент времени.

Значение фазы в начальный момент времени ( t 0 ) называется начальной

ψ
фазой. Начальная фаза это ближайшая от начала осей координат точка перехода от отрицательных значений мгновенных величин синусоид к положительным значениям. Если эта точка располагается слева от оси ординат, то фаза берется со знаком "+", если справа от нее – со знаком "-".

u

i
Разность ψ φ– называется сдвигомфаз; в частности, на рис.5.1

напряжение uопережает ток iна величину φ.

Величина называется угловойчастотойи характеризует собой скорость изменения фазового угла.

Так как фазовый угол синусоиды за время одного периода Tизменяется на

2 π, то угловая частота

_ω_2 π

T

 2 π f.

Получение синусоидальной ЭДС

Переменный ток промышленной частоты (50 Гц) создают синхронные генераторы трехфазного тока, в которых используется явление электромагнитной индукции. С помощью генератора механическая энергия, получаемая от первичного двигателя (турбины), преобразуется в электрическую энергию переменного тока.

Синхронный генератор состоит из неподвижного статора и подвижного ротора (рис.5.2).

Статор – полый цилиндр с пазами для проводников, соединенных специальным образом. Изготавливается из листовой электротехнической стали.

Ротор – электромагнит, возбуждаемый постоянным током. Ток возбуждения подается от возбудителя по проводам через щетки на медные кольца, укрепленные на валу ротора. Возбудитель – небольшой генератор постоянного тока.

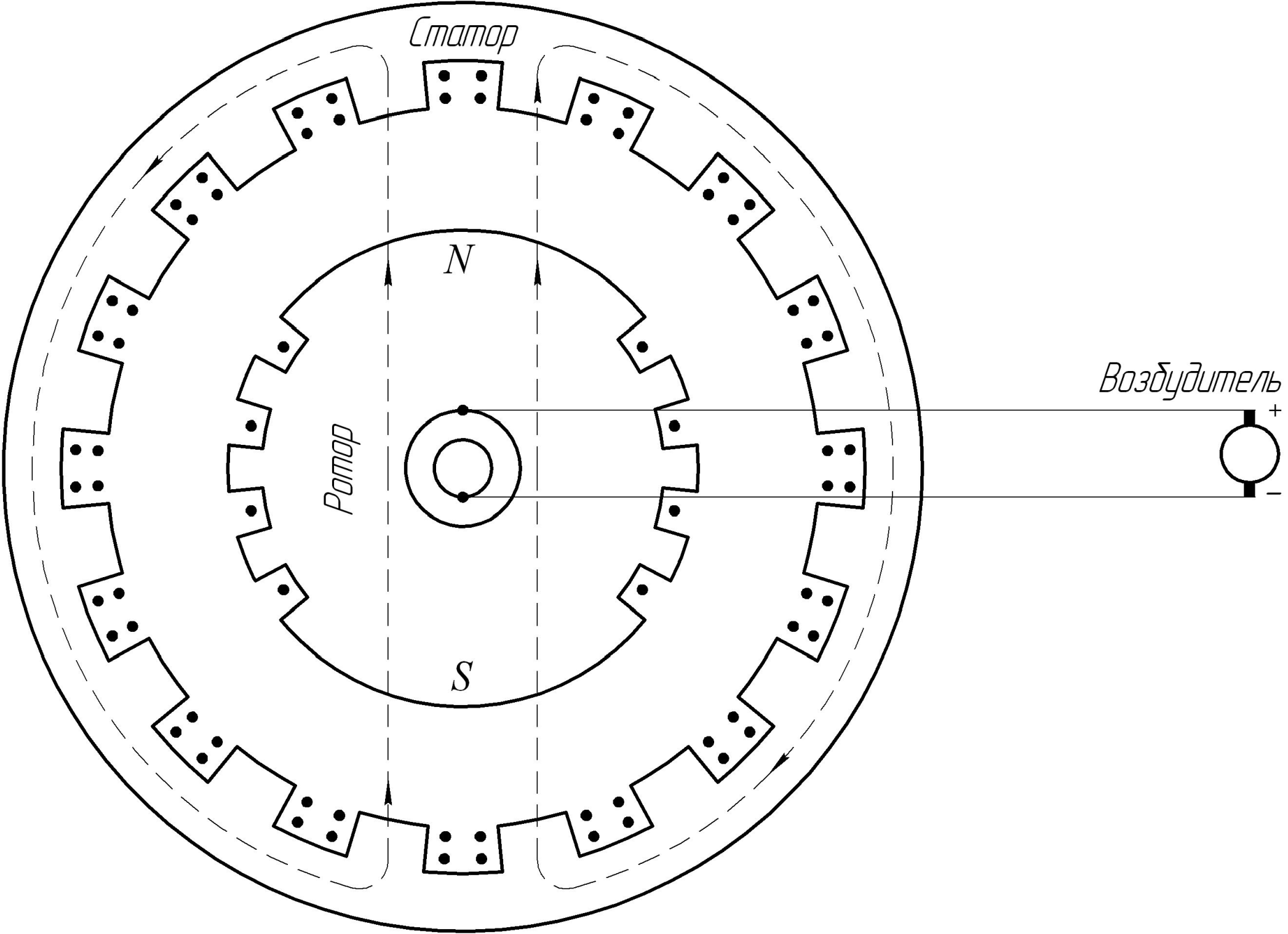
Рис.5.2
Магнитный поток ротора проходит через тело ротора, два воздушных промежутка между статором и ротором и сердечник статора.

При вращении ротора этот магнитный поток пересекает проводники статора и индуктирует в них переменную ЭДС:

e B l v,

где B – магнитная индукция, l – активная длина проводника (охватываемая магнитным полем), v – окружная скорость (магнитного потока по отношению к проводнику).

В данной формуле

l, v const. Следовательно, изменение ЭДС eпри

вращении ротора вызывается только изменением магнитной индукции B. Если