Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 428

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

УДК 621.3

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 97

ВВЕДЕНИЕ

Понятие о линейных и нелинейных элементах и цепях

Индуктивность

Основные определения, относящиеся к топологии электрической цепи

Режимы работы электрической цепи

АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Метод узловых потенциалов

Метод двух узлов

Метод эквивалентного генератора

Баланс мощности

АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Получение синусоидальной ЭДС

Представление синусоидальных величин комплексными числами

Некоторые операции с комплексными числами

Изображение производной синусоидальной функции

Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей

Законы Ома и Кирхгофа для синусоидальных цепей

Индуктивность в цепи синусоидального тока

Конденсатор в цепи синусоидального тока

Комплексная мощность Если известны напряжение и ток в цепи переменного тока, имеющие комплексные выраженияU  Um 2 ejψuи I Im ejψi, а также сдвиг фаз между ними φψuψi, то выражение полной комплексной мощности в данной цепиопределяется как произведение комплекса напряжения на сопряженный комплекс тока и имеет вид: S  U  I*  U ejψu I e jψi U I ej(ψuψi)  S U I ejφ U I cosφ jU I sinφ P j Q, гдеP ReU  I* , а Q ImU  I* ; – полная мощность ВА; P– активная мощность, измеряется в Вт, кВт, МВт; Q– реактивная мощность, измеряется в вольт-амперах реактивных ВАр, кВАр, МВАр. Рис. 5.23Треугольник мощностей на комплексной плоскости показан на рис. 5.23.Этот случай соответствует положительному значению реактивной мощности Q . 1   ...   23   24   25   26   27   28   29   30   ...   56

Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов

и UТреугольник сопротивлений

Треугольник проводимостей

Параллельное соединение.

Смешанное соединение.

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Последовательное соединение индуктивно связанных катушек при согласном и встречном включении

Входное сопротивление воздушного трансформатора

ТРЕХФАЗНЫЕ ЦЕПИ

7,1. Основные понятия. Способы изображения симметричной трехфазной

Соединение фаз трехфазного источника питания звездой и

Трехфазные цепи с симметричными пассивными приемниками

Соединение треугольником

Трехфазные цепи с несимметричными пассивными приемниками

Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником

Мощность в трехфазной цепи

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

8.1 Основные понятия

Короткое замыкание RL цепи постоянного тока

Отключение цепи RL от источника постоянного напряжения

8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )

8.3.3. Релаксационный генератор

МАГНИТНЫЕ ЦЕПИ

Расчет неразветвленной магнитной цепи

Обратная задача.

Катушка индуктивности с ферромагнитным сердечником У катушки без сердечника магнитный потокФ B Sпропорционален магнитной движущей силеF I w, а зависимость Ф(I)является линейной. При наличии магнитопровода магнитный поток катушки (дросселя) значительно возрастает при прочих равных условиях, т.к. он создается не только катушкой с током (источником внешнего магнитного поля), но и соответствующим ферромагнитным веществом магнитопровода (источником внутреннего магнитного поля).Известно, Ф B S μ H S, т.е. Ф μ, а для ферромагнитных материалов на несколько порядков выше магнитной проницаемости воздухаμ0 . Значит, одинаковый магнитный поток в катушке с магнитопроводом можно получить призначительно меньшей намагничивающей силе F I  w.Схема замещения реальной катушки индуктивности имеет вид рис.9.12. Здесь i0Рис.9.12 Рис.9.13 ток катушки; R- активное сопротивление проводов катушки; x ω L индуктивное сопротивление катушки; R0 - активное сопротивление, обусловленное потерями мощности в катушкеR PM;0 I2x0 - индуктивное сопротивление, обусловленное основным магнитным потоком. По второму закону КирхгофаU  R I jx I E . 0 0Векторная диаграмма, построенная в соответствии с данным уравнением, имеет вид (рис.10.13). Так какe  dФ, то Ф отстает по фазе от E наdtπ. Кроме того,2 0Ф отстает по фазе от тока I на угол δвследствие явления гистерезиса. Так как зависимостьB(H)– нелинейная, следовательно нелинейной будет и зависимость Ф(i0 ) (рис.9.14). Так как напряжение зависимость Ф(t) .u(t)Рис.9.14синусоидальное, значит синусоидальной будет и Но из-за нелинейностиB(H)ток катушки с сердечникомi0 (t)будет несинусоидальным (см. рис.9.14), а это значит, что нелинейная индуктивность является генератором высших гармоник тока. Из рис. 9.14 видно, что ток i0опережает по фазе поток Фна гистерезисный угол δ(ток достигает нуля раньше магнитного потока).Для катушки индуктивности с магнитопроводом, имеющим воздушный зазор (рис.9.15), по закону ОмаФ F,Rм гдеRмопределяются, в основном, сопротивлением воздушного зазора. Рис. 9.15 Рис.9.16 Увеличение воздушного зазора увеличиваетRм, а значит должно уменьшить поток Ф. Но этого не происходит, т.к. из формулыU 4,44  f w Фmследует, что ФmU4,44  f w, т.е. величина потока зависит только от действительного значения питающего напряжения, которое, естественно, не меняется. Значит, не меняется и поток. Это объясняется тем, что при увеличении δувеличивается намагничивающая силаI wдо значения, при котором поток Ф(а значит и отношениеF) остаетсяRм постоянным. Ток дросселя увеличивается за счет того, что уменьшается полное сопротивление катушки вследствие уменьшения ее реактивного сопротивления (из- за уменьшения индуктивности) (см. рис.9.16).Таким образом, путем изменения величины воздушного зазора в магнитопроводе, можно регулировать ток катушки индуктивности (дросселя) при включении ее в цепь переменного тока при неизменности питающего напряжения. В данном случае, катушка индуктивности с ферромагнитным сердечником, в цепи которого имеется регулируемый воздушный зазор, выполняет функции регулируемого сопротивления. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Башарин С.А., Федоров В.В. Теоретические основы электротехники. Учебное пособие. М.: ACADEMA. 2004. – 304с. Иванов И.И., Соловьев Г.И., Равдоник В.С. Электротехника. Учебник. 3-е изд., стер. – СПб.: Издательство «Лань», 2005. – 496с., ил. Касаткин А.С., Немцов М.В. Основы электротехники для студентов вузов. – М.: Энергоатомиздат, 2000. 1   ...   48   49   50   51   52   53   54   55   56


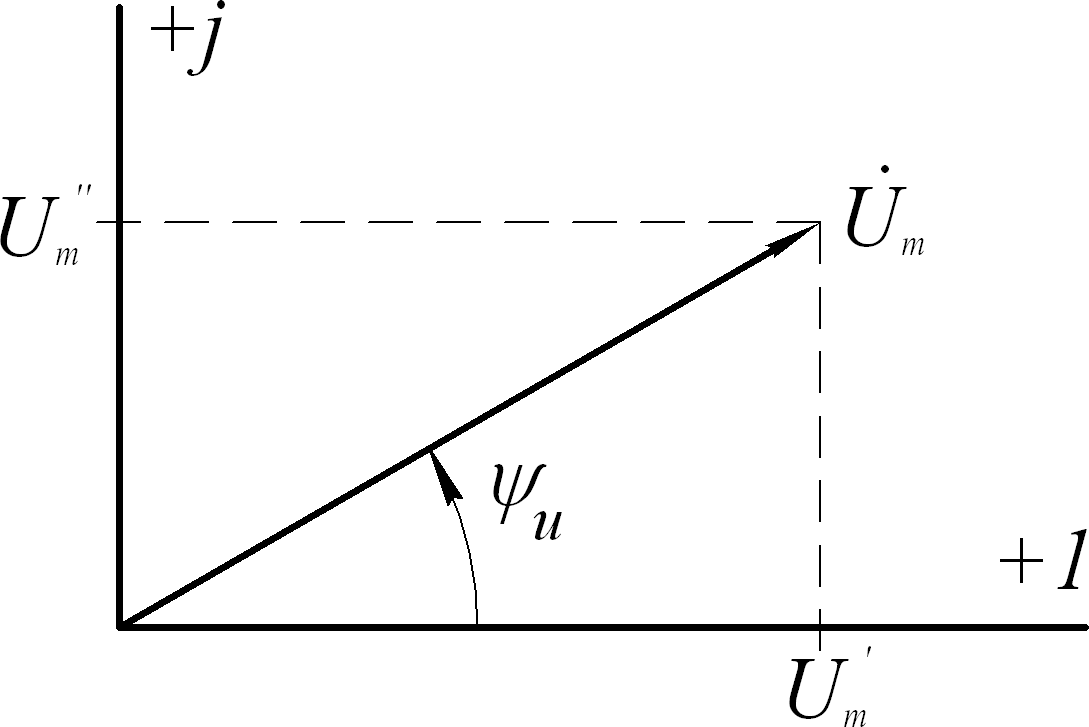форме, нужно изобразить данное число на комплексной плоскости и найти начальную

фазу ψu

  • угол, образуемый вектором

U mс

осью +1 и модуль вектора U m

(рис.5.8).

Так как вектор

U m

U

находится в первом


Рис.5.8

квадранте:

tgψ

m.


m
u U



m
m
В свою очередь, модуль вектора U m

можно рассчитать по формулам

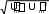U , либо U

U

U .





u
m
u
Окончательно U

m

m
U

m
jU
Um

m
ej(ωtψu) .

cosψsinψ

Если мгновенное значение напряжения задано в виде синусоиды u Umsin(ω tψu) , то комплексную амплитуду сначала записывают в показательной форме, а затем по формуле Эйлера переходят к алгебраической форме:

U m

Um

ejψu

Um

cosψu

  • j Um

sinψu

Um

  • jUm .

Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическим действиям над комплексными числами этих векторов.

        1. 1   ...   14   15   16   17   18   19   20   21   ...   56

Некоторые операции с комплексными числами



Известно, что

j 0 1 j 1 ej90 ej90 ;

j 0 1 j 1 e j90 e j90 .

Пусть дано комплексное число вида

A a
jb A ejψ.

Число



Aназывается сопряженнымпо отношению к комплексному числу A ,

если его модуль равен модулю числа A , а аргумент имеет противоположный знак,

т.е.



A a j b A e jφ

У сопряженных чисел:

A A*

 ;

Re A

* 1 A a;

Re A 2 A

   

JA J * 1 A b.

mm A 2 A

   

Формулы перехода от алгебраической формы записи комплексного числа к показательной и наоборот:

A| A |



a2 b2 ;

a


ψ

arctg;

b


Умножим вектор A на j:

a A cosψ;

b A sinψ.

A j A ejψ ej90 A ej(ψ90) .

Следовательно, умножение вектора на величину jдает вектор по модулю равный данному, но повернутый в сторону опережения (против часовой стрелки) на

90 по отношению к исходному (рис.5.9).

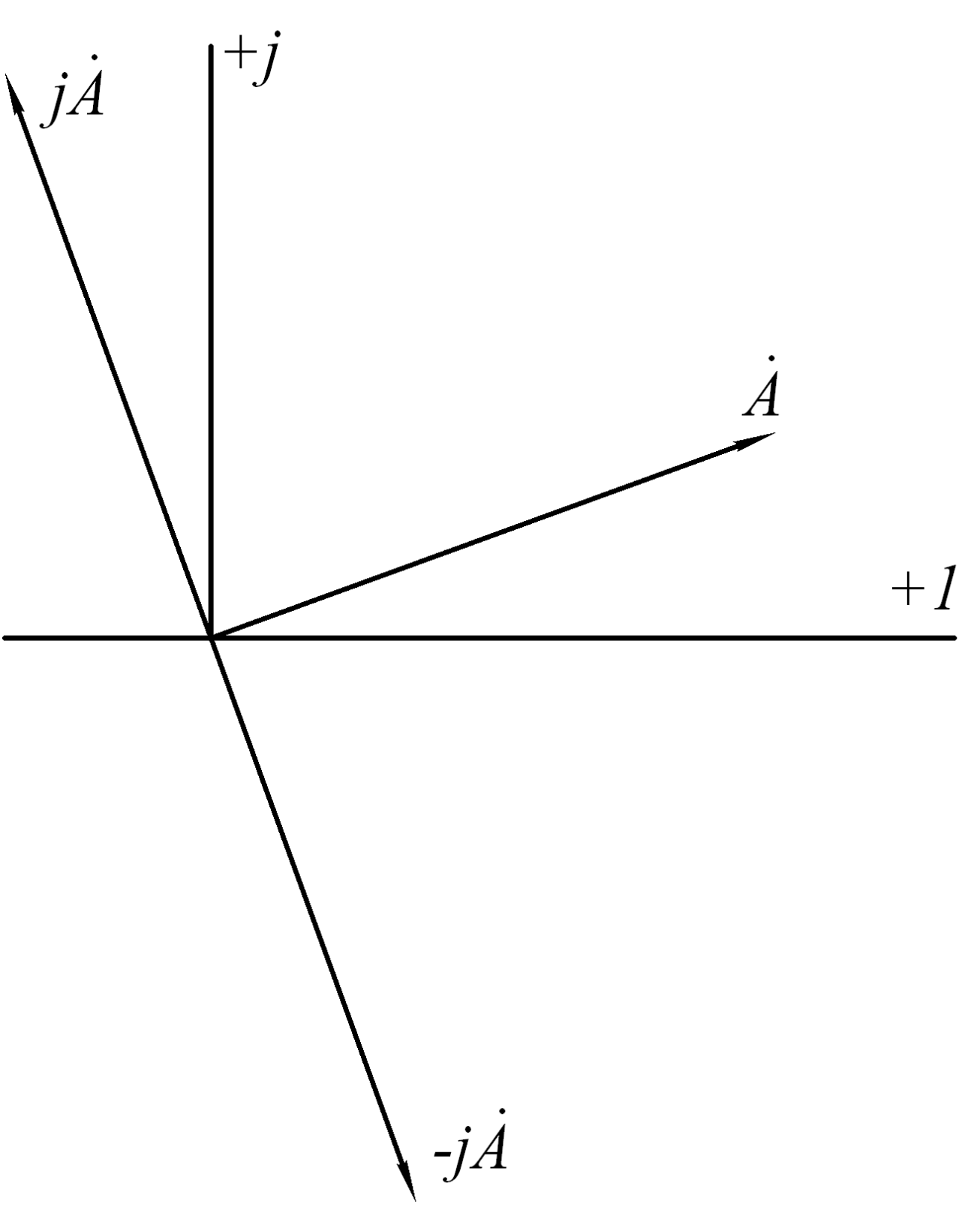Умножим вектор A на (-j):

A j A ejψ ej90 A ej(ψ90) .

Следовательно, умножение вектора на (-j) дает вектор, по модулю равный данному, но повернутый в сторону отставания (по часовой
стрелке)

на 90 по отношению к исходному (см.

рис.5.9).

Некоторые часто встречающиеся операции с j:

1 1

j ej90

e j90 j;


Рис.5.9

j j ej90 ej90 ej180 ;

ej180 cos 180 jsin 180 1, т.е.

j j j2 1.


        1. 1   ...   15   16   17   18   19   20   21   22   ...   56

Смотрите также файлы