Файл: Конспект лекций (часть 1) Составители А. М. Коленченко Е. Н. Коленченко саранск.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 427
Скачиваний: 4
СОДЕРЖАНИЕ
Понятие о линейных и нелинейных элементах и цепях
Основные определения, относящиеся к топологии электрической цепи
Режимы работы электрической цепи
АНАЛИЗ И РАСЧЕТ СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Метод эквивалентного генератора
АНАЛИЗ И РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Представление синусоидальных величин комплексными числами
Некоторые операции с комплексными числами
Изображение производной синусоидальной функции
Метод комплексных амплитуд (символический метод). Законы Кирхгофа для синусоидальных цепей
Законы Ома и Кирхгофа для синусоидальных цепей
Индуктивность в цепи синусоидального тока
Конденсатор в цепи синусоидального тока
Последовательное и параллельное соединения элементов R, L, C. Резонансы напряжений и токов
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СО ВЗАИМНОЙ ИНДУКТИВНОСТЬЮ ПОД ВОЗДЕЙСТВИЕМ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
Последовательное соединение индуктивно связанных катушек при согласном и встречном включении
Входное сопротивление воздушного трансформатора
7,1. Основные понятия. Способы изображения симметричной трехфазной
Соединение фаз трехфазного источника питания звездой и
Трехфазные цепи с симметричными пассивными приемниками
Трехфазные цепи с несимметричными пассивными приемниками
Трехфазная цепь с несимметричными пассивными приемниками, включенными треугольником
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Короткое замыкание RL цепи постоянного тока
Отключение цепи RL от источника постоянного напряжения
8.3.2 Короткое замыкание цепи RC (разряд конденсатора С на сопротивлении R )
8.3.3. Релаксационный генератор
д
I2
T
T
1
i2 dt.
0
Умножив обе части полученного выражения на величину
T
д
R T, получим:
I2 R T R i2 dt.
0
Полученное выражение дает право утверждать, что:
действующее значение периодического тока равно по величине такому постоянному току, который проходя через неизменное сопротивление R за период T , выделяет такое же количество теплоты, что и данный периодический ток i .
Получим численное значение для
Iд, если известно амплитудное значение
тока (5.3)
Im. Преобразуем выражение, находящееся под знаком "корень квадратный" в
TT
i2 dt
I2 sin 2 ωt dt I2
T2 T
I
2
sin 2 ωt dt m
2 T
I
(1 cos 2ωt) dt m
dt
T
cos 2ωtdt
m
0 0
m
0 0
2 0 0
I2 T 1
T I2 1
2 π
I2
m t
sin 2 ω t
m T sin 2
T sin 0 m
T.
2 0
2 ω
0 2
2 ω T
2
Подставив полученное значение в исходное выражение (5.3), получим
 I
II
m
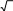 2
2 0,707 Im.
Аналогично можно получить выражения для определения действующих значений напряжения Uи ЭДС E, которые примут вид:
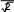
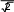 U Um; E Em.
U Um; E Em.- 1 ... 19 20 21 22 23 24 25 26 ... 56
Простейшие линейные цепи однофазного синусоидального тока
-
Резистивный элемент в цепи синусоидального тока
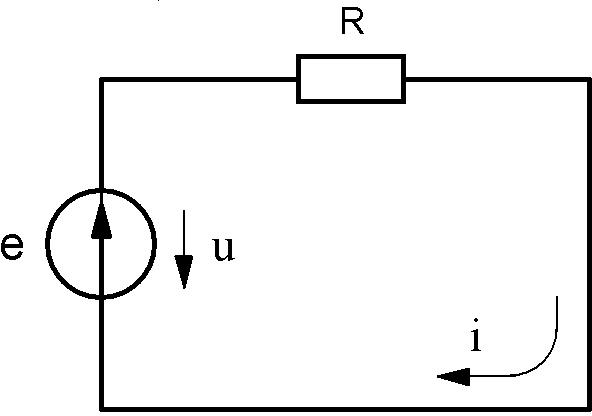 Пусть на входе цепи (рис.5.13) действует напряжение
Пусть на входе цепи (рис.5.13) действует напряжениеu Umsin(ω tψu) .
Требуется определить изменение тока и мощности в этой цепи.
По закону Ома
i u
R
Um
R
sin(ω tψu
) , т.е.
Рис.5.13
синусоида тока имеет ту же частоту и начальную фазу напряжения и, что важно
заметить,
ψiψu.
Следовательно, на резисторе мгновенные значения тока iи напряжения u
имеют одинаковую частоту и совпадают по фазе, т.е. i Im sin(ω tψi) .
Мгновенное значение мощности этой цепи равно произведению мгновенных значений iи u :
p u i Um
Im
sin 2 (ω tψ
) Um
Im
1 1 cos 2 (ω tψ
2
u)
u
Um Im
2
-
Um Im cos 2 (ω t
2
-
ψu
) UI UIcos 2(ωtψu).
 Следовательно, мгновенная мощность в данной цепи имеет постоянную
Следовательно, мгновенная мощность в данной цепи имеет постояннуюсоставляющую
Um Im
2
и составляющую
Um Im cos 2 ωt
2
, изменяющуюся с
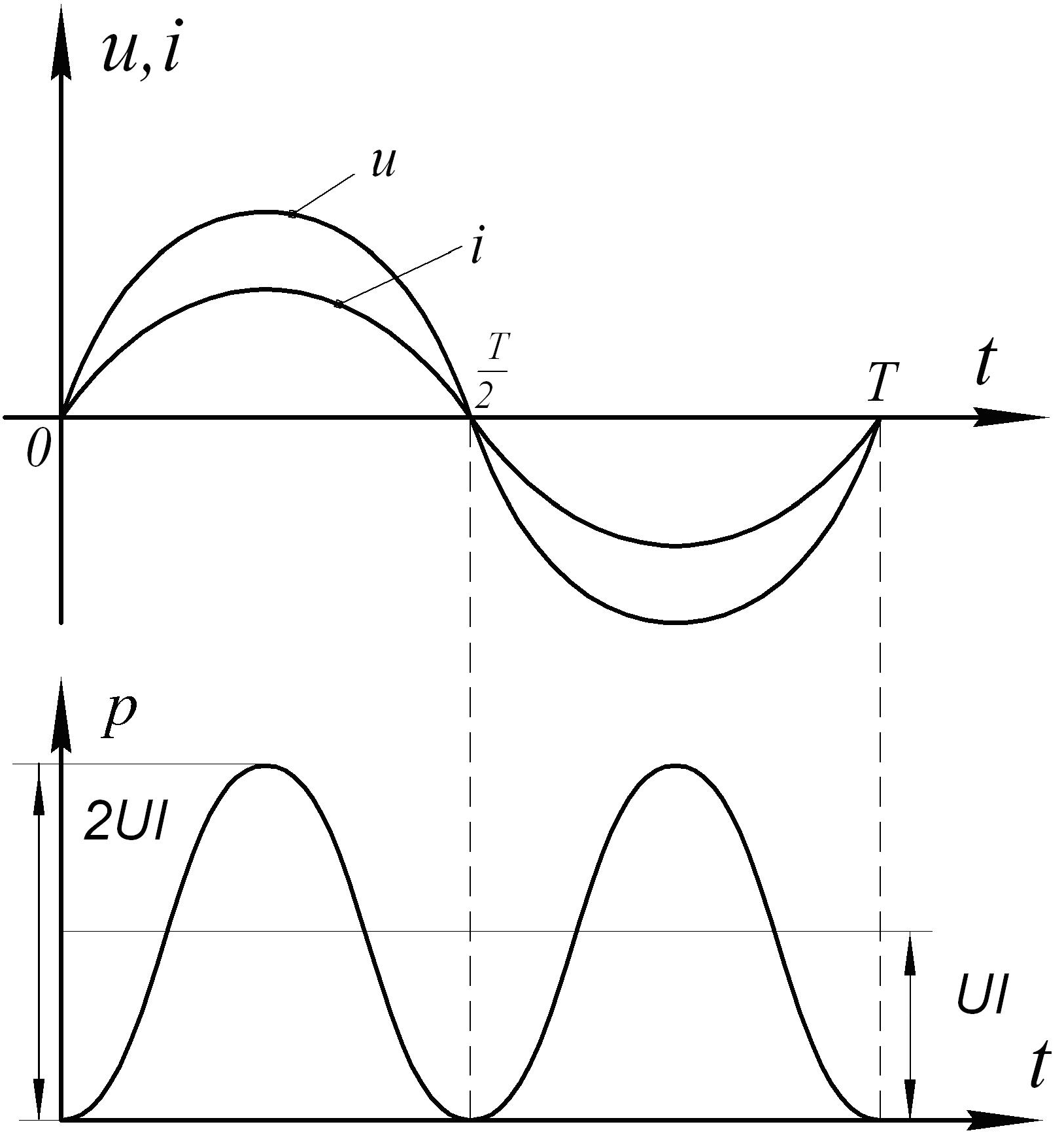
частотой 2 ω. Графики зависимостей u,
Рис.5.14
iи pот времени имеют вид (рис.5.14).Из графиков видно, что мгновенная мощность, несмотря на пульсации остается положительной.
Следовательно, при любом направлении
тока, поступающая энергия на активном сопротивлении превращается в тепловую энергию.
1 T
Среднее за период значение мощности
P
pdt U I
или
P R I2 ,
T0
что совпадает с выражением для активной мощности цепи. Запишем выражения для uи iв комплексном виде:
.
m
u. U
ejωt;
i. I
ejωt.
.
m
На рис.5.15 построена векторная диаграмма для амплитудных значений.
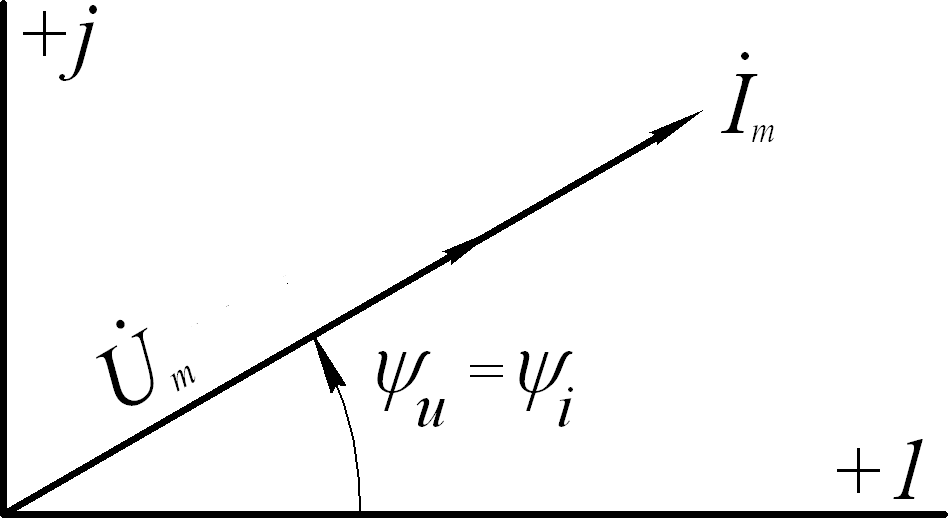
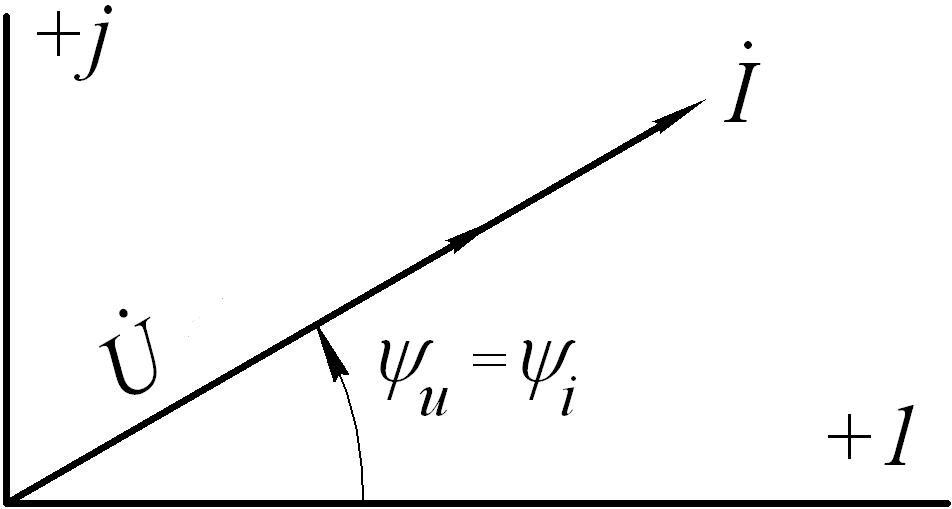
Рис.5.15 Рис.5.16
Из диаграммы видно, что вектор синусоидального напряжения на резисторе
совпадает по фазе с вектором синусоидального тока.
При расчете синусоидальных цепей принято строить векторные диаграммы для комплексных действующих значений U и I . Они совпадают по направлению с
векторами U m
и I и отличаются лишь по величине:
m
m
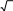 I I
I I 2
I e
jψu
I e
jψi;
U
U m
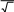 2
2 U e
jψu
R I e
jψu
R I.
Векторная диаграмма для действующих значений U и I показана на рис. 5.16.